doc-Format - Evangelische Friedrich Oberlin Fachoberschule
Werbung
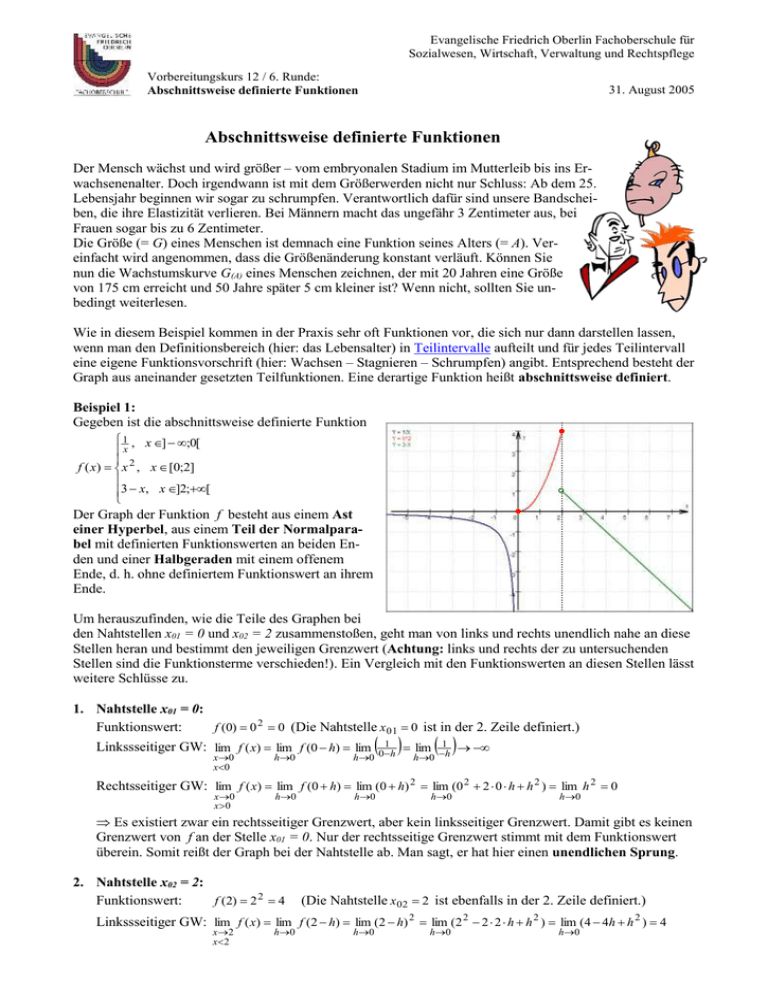
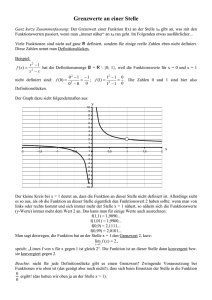
Evangelische Friedrich Oberlin Fachoberschule für Sozialwesen, Wirtschaft, Verwaltung und Rechtspflege Vorbereitungskurs 12 / 6. Runde: Abschnittsweise definierte Funktionen 31. August 2005 Abschnittsweise definierte Funktionen Der Mensch wächst und wird größer – vom embryonalen Stadium im Mutterleib bis ins Erwachsenenalter. Doch irgendwann ist mit dem Größerwerden nicht nur Schluss: Ab dem 25. Lebensjahr beginnen wir sogar zu schrumpfen. Verantwortlich dafür sind unsere Bandscheiben, die ihre Elastizität verlieren. Bei Männern macht das ungefähr 3 Zentimeter aus, bei Frauen sogar bis zu 6 Zentimeter. Die Größe (= G) eines Menschen ist demnach eine Funktion seines Alters (= A). Vereinfacht wird angenommen, dass die Größenänderung konstant verläuft. Können Sie nun die Wachstumskurve G(A) eines Menschen zeichnen, der mit 20 Jahren eine Größe von 175 cm erreicht und 50 Jahre später 5 cm kleiner ist? Wenn nicht, sollten Sie unbedingt weiterlesen. Wie in diesem Beispiel kommen in der Praxis sehr oft Funktionen vor, die sich nur dann darstellen lassen, wenn man den Definitionsbereich (hier: das Lebensalter) in Teilintervalle aufteilt und für jedes Teilintervall eine eigene Funktionsvorschrift (hier: Wachsen – Stagnieren – Schrumpfen) angibt. Entsprechend besteht der Graph aus aneinander gesetzten Teilfunktionen. Eine derartige Funktion heißt abschnittsweise definiert. Beispiel 1: Gegeben ist die abschnittsweise definierte Funktion 1 , x ] ;0[ x f ( x) x 2 , x [0;2] 3 x, x ]2;[ Der Graph der Funktion f besteht aus einem Ast einer Hyperbel, aus einem Teil der Normalparabel mit definierten Funktionswerten an beiden Enden und einer Halbgeraden mit einem offenem Ende, d. h. ohne definiertem Funktionswert an ihrem Ende. Um herauszufinden, wie die Teile des Graphen bei den Nahtstellen x01 = 0 und x02 = 2 zusammenstoßen, geht man von links und rechts unendlich nahe an diese Stellen heran und bestimmt den jeweiligen Grenzwert (Achtung: links und rechts der zu untersuchenden Stellen sind die Funktionsterme verschieden!). Ein Vergleich mit den Funktionswerten an diesen Stellen lässt weitere Schlüsse zu. 1. Nahtstelle x01 = 0: Funktionswert: f (0) 0 2 0 (Die Nahtstelle x 01 0 ist in der 2. Zeile definiert.) Linkssseitiger GW: lim f ( x) lim f (0 h) lim x0 x 0 h0 hlim 1 0 h 1 h0 0h Rechtsseitiger GW: lim f ( x) lim f (0 h) lim (0 h) 2 lim (0 2 2 0 h h 2 ) lim h 2 0 x 0 x 0 h0 h0 h0 h0 Es existiert zwar ein rechtsseitiger Grenzwert, aber kein linksseitiger Grenzwert. Damit gibt es keinen Grenzwert von f an der Stelle x01 = 0. Nur der rechtsseitige Grenzwert stimmt mit dem Funktionswert überein. Somit reißt der Graph bei der Nahtstelle ab. Man sagt, er hat hier einen unendlichen Sprung. 2. Nahtstelle x02 = 2: Funktionswert: f (2) 2 2 4 (Die Nahtstelle x02 2 ist ebenfalls in der 2. Zeile definiert.) Linkssseitiger GW: lim f ( x) lim f (2 h) lim (2 h) 2 lim (2 2 2 2 h h 2 ) lim (4 4h h 2 ) 4 x 2 x2 h0 h0 h0 h0 Rechtsseitiger GW: lim f ( x) lim f (2 h) lim (3 2 h) lim (1 h) 1 x 2 x 2 h0 h0 h0 Da die einseitigen Grenzwerte verschieden sind, existiert kein Grenzwert von f an der Stelle x02 = 2. Nur der linksseitige Grenzwert stimmt mit dem Funktionswert überein. Somit reißt der Graph ebenfalls bei der Nahtstelle ab. Man sagt, er hat hier einen endlichen Sprung. Sie wissen nun, die Teile des Graphen gehen nicht nahtlos ineinander über, d. h. er hat Sprungstellen. Ganz anders sieht das bei folgender Funktion aus. Beispiel 2: Gegeben ist die abschnittsweise definierte Funktion 3 x, x ] ;2[ f ( x) 2 2 x x 1, x [2;[ Der Graph der Funktion f besteht aus einer Halbgeraden mit offenem Ende und aus dem Teil einer Parabel mit einem offenen und einem geschlossenen Ende. Interessant ist das Verhalten des Graphen an der Nahtstelle x 0 2 : f (2) (2) 2 (2) 1 3 Funktionswert: Linkssseitiger GW: Rechtsseitiger GW: (Die Nahtstelle x 0 2 ist in der 2. Zeile definiert.) lim f ( x) lim g (2 h) lim 32 (2 h) lim 3 32 h 3 h0 h0 h0 x2 x2 lim f ( x) lim f (2 h) lim (( 2 h) 2 (2 h) 1) lim (4 4h h 2 2 h 1) 3 x2 x 2 h0 h0 h0 Die einseitigen Grenzwerte existieren und stimmen überein. Also gibt es einen Grenzwert von f an der Stelle x 0 2 . Er hat den Wert 3 und ist gleich dem Funktionswert f ( x 0 ) . Anschaulich bedeutet das, die Funktion f hat hier keine Sprungstelle. Beim Zeichnen des Graphen braucht der Stift an dieser Stelle nicht vom Papier abgehoben zu werden. Man sagt, der Graph ist an der Nahtstelle lokal stetig. Mathematisch sieht das so aus: Definition: Eine Funktion f : Df IR heißt lokal stetig bei x0 D f , genau dann, wenn der Grenzwert lim f ( x) existiert und mit dem Funktionswert f ( x 0 ) übereinstimmt. x x0 Funktionen mit Sprungstellen sind unstetig (s. Bsp. 1). Definition: Eine Funktion f heißt stetig (genauer: „global stetig“), wenn f an jeder Stelle x0 D f stetig ist. Bei einem offenen Intervall ist es kein Problem, eine Funktion an einer Stelle x0 auf Stetigkeit zu untersuchen. Man nähert sich von zwei Seiten der Stelle x0 und überprüft, ob der gleiche Wert wie an dieser Stelle selbst herauskommt. Liegt nun x0 D f genau am Rand eines abgeschlossenen Intervalls, so ist nur eine Annäherung von einer Seite möglich. Man definiert daher: Definition: Eine Funktion f : [a; b] IR heißt rechtsseitig stetig bei a, wenn der rechtsseitige Grenzwert existiert und mit dem Funktionswert f (a ) übereinstimmt. Analog gilt: f ist linksseitig stetig bei b, wenn der linksseitige Grenzwert existiert und mit dem Funktionswert f (b) übereinstimmt. (s. abgeschlossenes Teilintervall I [0;2] aus Bsp. 1) Anschaulich heißt das, ist der Graph einer Funktion in einem abgeschlossenen Intervall stetig, lässt er sich in einem Zug zeichnen. Ausgehend von dieser Vorstellung können Sie sich abschließend den Zwischenwertsatz, Nullstellensatz und Extremwertsatz leicht plausibel machen.