Lernpfad "Integralrechnung"
Werbung

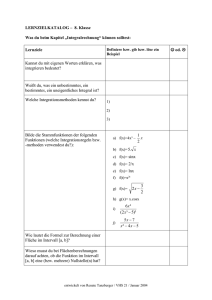
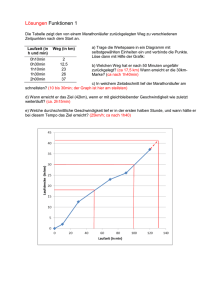
Integralrechnung: Ein großes Anwendungsgebiet der Integralrechnung ist die Flächen- und Volumsberechnung. Gehen Sie zu http://members.chello.at/gut.jutta.gerhard/kurs/integral1.htm. Zunächst werden Stammfunktionen definiert (das Auffinden der Stammfunktion, auch integrieren genannt, ist die Umkehroperation zum Differenzieren). Die Stammfunktion wird auch als unbestimmtes Integral bezeichnet. Dann werden Stammfunktionen einiger wichtiger Funktionen gebildet (dass diese stimmen, können Sie kontrollieren: Wenn Sie die Stammfunktion differenzieren, muss die Funktion rauskommen). Machen Sie ein paar Übungen von http://members.chello.at/gut.jutta.gerhard/kurs/stammf.htm (dort finden Sie auch die Lösungen zum Anklicken). Auf http://members.chello.at/gut.jutta.gerhard/kurs/integral2.htm geht es mit dem bestimmten Integral weiter und dies führt zur Berechnung von Flächen. Abschließend gibt es eine Formel zur Berechnung des Volumens eines Körpers, der durch Rotation um die x-Achse bzw. yAchse entsteht. Auf http://members.chello.at/gut.jutta.gerhard/kurs/integral_ueb.htm folgen Übungen zu bestimmten Integralen, Flächen- und Volumsberechnungen – machen Sie doch ein paar davon (die Lösungen sind dort zum Anklicken). Alternativ oder ergänzend zu den vorigen Websites können Sie sich für die Themen Stammfunktionen (=unbestimmtes Integral) und Flächeninhalt (= bestimmtes Integral) auch die Unterpunkte auf www.mathe-profis.de/index.php?page=klasse_12/integralrechnung anschauen. Vielleicht entspricht ihnen diese Darstellung mehr? Oder Sie schauen sich die Seite www.mathe-online.at/mathint/int/i.html an, die einen sehr ausführlichen Überblick geben, wobei die Volumsberechnung noch fehlt und die Partialbruchzerlegung nicht ausreichend erklärt ist. Oder Sie gehen einfach zum nächsten Punkt weiter: Im Unterschied zum Differenzieren, wo es mit Hilfe der Differentationsregeln relativ leicht ist, auch komplizierte Funktionen zu differenzieren, ist das Integrieren wesentlich schwieriger bzw. lassen sich manche Integrale auch mit den Methoden, die Sie gleich kennen lernen werden, nicht finden (aber solche kommen ja dann auch nicht zur Prüfung). Die Integrationsmethoden, um die es nun gehen soll, lauten Substitutionsmethode Partielle Integration Partialbruchzerlegung Die drei Methoden werden auf der nachfolgenden Website präsentiert: http://ilias.vhs21.ac.at/2bw/mathe/themen/Int/TH_UE_IntegrationsmethodenM3_Gurtner_SS06.doc Auf der Website http://archives.math.utk.edu/visual.calculus/4/substitutions.3/ wird (auf Englisch) die Substitutionsmethode Schritt für Schritt vorgeführt. Wenn Sie sich mit den Methoden ein wenig auskennen, probieren Sie die Beispiele auf http://ilias.vhs21.ac.at/2bw/mathe/themen/Int/AB_IntegrierenDifferenzieren_Tanzberger_WS03.doc - hier geht es darum, zu differenzieren und zu integrieren und dabei die verschiedenen Regeln und Methoden anzuwenden. Die Lösungen finden Sie auf http://ilias.vhs21.ac.at/2bw/mathe/themen/Int/AB_IntegrierenDifferenzierenLsg_Tanzberger_WS06.doc Vier letzte Formeln wollen wir Ihnen nicht vorenthalten, da diese laut Themenbereichskatalog bei der AHS-ExternistInnenprüfung verlangt werden können. Die Formeln finden Sie üblicherweise auch in Ihrer Formelsammlung: Die Berechnung einer Kurvenlänge erfolgt nach der Formel: b l 1 [ f ' ( x)]² dx a Dazu ein Beispiel: Gesucht ist die Länge des Kurvenbogens, der durch die Funktion f: y² = x³ im Intervall von 0 bis 4 gegeben ist. Um in die Formel einsetzen zu können, brauche ich zunächst f(x). Das ist hier x ³ . Als 1 2 3 3 .x x 2 2 9 Nun soll das Ganze quadriert werden [f’(x)]² = x 4 4 9 In die Formel eingesetzt ergibt das l 1 x dx 4 0 nächstes soll ich f’(x) bilden f’(x) = 10 Ich substituiere (t= 1 4 9 4 2 x ) und erhalte dadurch l t dt l . t³ 4 9 3 91 4 4 2 9 Rücksubstituiert ergibt das l . (1 x) 3 4 9 3 0 Wenn ich nun die Grenzen einsetze, erhalte ich l 8 9 3 9 3 (1 .4) (1 .0) 9,07 LE 27 4 4 Formel für die Koordinaten des Schwerpunktes S(/) eines Flächenstückes, das y=f(x) mit der x-Achse einschließt: b b x. ydx a b und 1 y² dx 2 a b ydx ydx a a Da die beiden Nenner gleich sind, reicht es, sie ein Mal auszurechnen. Das schaut komplizierter aus als es ist, daher kurz ein vorgerechnetes Beispiel dazu: Gesucht ist der Schwerpunkt jener Fläche, die durch die Parabel y = x2 − 4 und die x-Achse begrenzt ist. Aus 0 = x² - 4 ergeben sich die beiden Grenzen a=-2 und b=2. Dass der x-Wert des Schwerpunkts 0 sein wird, „sehe“ ich; zu Übungszwecken berechne ich die Koordinate. Der y-Wert des Schwerpunkts wird wohl zwischen -1 und -2 liegen. Der genaue Wert muss berechnet werden. 2 2 2 x.( x² 4)dx ( x³ 4 x)dx 2 2 ( x² 4)dx 2 2 2 ( x² 4)dx 2 x4 2 x² 4 2 2 x3 4x 3 2 (4 8) (4 8) 0 =0 8 8 8 8 3 3 2 2 1 x 5 8x³ 1 4 16 x ( x 8 x ² 16 )² dx 2 5 3 2 2 2 2 16 8 8 16 8 8 2( x² 4)dx 3 3 3 2 1 ( x ² 4)² dx 2 2 1 32 64 1 32 64 . 32 . 32 128 128 2 5 3 3 2 5 15 15 256.3 8 = -1,6 32 32 15.32 5 3 3 Der Schwerpunkt hat die Koordinaten S(0/-1,6). Formel für die Koordinaten des Schwerpunktes S(/) eines Flächenstückes, das von zwei Kurven eingeschlossen wird (a und b sind die x-Koordinaten der Schnittpunkte der beiden Kurven): b b 1 x .[ f ( x ) g ( x )] dx [ f ²( x) g ²( x)]dx a 2 a und b b [ f ( x) g ( x)]dx [ f ( x) g ( x)]dx a a Beispiel: Berechnen Sie den Schwerpunkt jener Fläche, die von den beiden Parabeln y² = 2x uns x² = 2y im 1. Quadranten eingeschlossen wird. Zunächst berechne ich die Schnittpunkte S(0/0) und S(2/2). Damit haben ich die Grenzen a=0 und b=2. Für f(x) forme ich die „Oben liegende“ Parabel nach y um y= 2 x . Für g(x) muss ich die „unten x² liegende“ Parabel nach y umformen y= 2 Nun setze ich in die Formeln ein: 2 5 3 2 2 x4 x3 x² 2 0 x.[ 2 x 2 ]dx 0 2.x 2 dx 2. 5 x 8 0 1,2 0 2 2 . 0,9 = 0,9 2 1 3 x² x ² 0 [ 2 x 2 ]dx 2.x 2 2 dx 2. 2 .x 2 x³ 1, 3 0 3 6 0 0 2 2 2 1 [ f ²( x) g ²( x)]dx 2 0 2 2 1 x [2 x ]dx 20 4 1 x5 . x ² 2 20 0 1 .2,4 2 1,8 = 0,9 . 1, 3 . x² 1, 3 [ f ( x ) g ( x )] dx [ 2 x ] dx 0 0 2 Der Schwerpunkt des eingeschlossenen Flächenstücks hat die Koordinaten S(0,9/0,9). 2 4 2 Formel für die Koordinaten des Schwerpunktes S(/0) eines Körpers, der bei Drehung um die x-Achse entsteht: b x. y ²dx a b y ²dx a Beispiel: Gesucht ist der Schwerpunkt des Körpers, der entsteht, wenn die Parabel y² = 2x im Intervall, von 0 bis 2 um die x-Achse rotiert. 2 2 2 x.(2 x)dx 2 x²dx 0 2 0 2 (2 x)dx (2 x)dx 0 0 x³ 2. 3 0 2 x² 0 16 . 3 1, 3 Schwerpunktes des Körpers S(1,33/0) 4 So, damit haben wir einen Großteil des Stoffes dieses Kapitels abgedeckt. Es fehlen nur noch die „uneigentlichen Integrale“. Lesen Sie sich dazu das Kapitel auf www.matheonline.at/mathint/int/i.html#uneigInt durch. Hier finden Sie weitere Websites mit Übungsbeispielen zum Kapitel Integralrechnung: Auf http://www.mathe-online.at/tests/int/grundlegendes.html finden Sie einen Multiple Choice-Test zum Thema „Integrieren“ Beispiele von Stammfunktionen finden Sie auf www.zum.de/Faecher/M/NRW/pm/mathe/stammfkt.htm. Sie könnten einfach die rechte Seite umklappen, versuchen ein paar Beispiele zu lösen und mit der Lösung in der rechten Spalte kontrollieren. Auf der Website www.zum.de/Faecher/M/NRW/pm/mathe/bestint.htm finden sich Übungsbeispiele zu bestimmten Integralen (sind großteils ohne die oben genannten drei Integrationsmethoden zu lösen). Es geht nur darum mit der Formel b f ( x)dx F(b) – F(a) das bestimmte Integral zu berechnen, nicht darum die Fläche a zwischen Kurve und x-Achse im gegebenen Intervall zu bestimmen (der Unterschied zeigt sich z.B. bei f(x)=x³, wo das bestimmte Integral in den Grenzen von -5 bis 5 Null ist, die Fläche aber 312,5 AE). Auf www.zum.de/Faecher/M/NRW/pm/mathe/inhint.htm geht es nun wirklich um die Berechnung der Fläche! Einen Klapptest zum Thema Flächenberechnung zwischen Kurve und x-Achse bzw. zwischen zwei Kurven finden Sie auf www.thomas-unkelbach.de/m/a/fb/fb_1c_kt.pdf. und www.thomas-unkelbach.de/m/a/fb/fb_2b_kt.pdf, wobei Sie auf der rechten Seite auch kontrollieren können, ob Sie die Grenzen richtig bestimmt haben. Vorsicht: die Variable ist hier nicht immer x! Auf der Website http://ilias.vhs21.ac.at/2bw/mathe/themen/Int/UE_IntegralrechnungAnwendungen_Hochmann_SS04.pdf finden sich v.a. Übungsbeispiele zu Flächenberechnungen! Hier finden Sie noch einige anspruchsvollere Aufgaben (+ Lösungen): Auf www.mathe-cd.de/4_Funktionen/48_Integral/48001%20Lebla%20Int1%20CC.pdf finden Sie Aufgaben mit bestimmten Integralen, wobei Sie die neben den Stammfunktionen auch diverse Integrationsmethoden anwenden können müssen. http://ilias.vhs21.ac.at/2bw/mathe/themen/Int/UE_KD_mit_Integral_Gut_SS05.pdf Kurvendiskussionen inkl. Flächen- bzw. Volumsberechnungen www.math.ethz.ch/~kirchgra/matcoach/aufgabenliste.html Schauen Sie sich die Beispiele Nr. 4, 5, 6 von der Aufgabenliste an – toll ist, dass sich nach Anklicken der Aufgabe mehrere Fenster öffnen und so z.B. Veranschaulichung, Lösungshinweise, -weg, einfachere Beispiele,... extra angeklickt werden können! http://ilias.vhs21.ac.at/2bw/mathe/themen/Int/UE_umgekehrteKDmitIntegral_Tanzber ger_WS03.doc Umgekehrte Kurvendiskussionen mit Integral TIPP!! Auf www.arndt-bruenner.de/mathe/scripts/integral1.htm finden Sie einen Rechner für bestimmte Integrale (Vorsicht, falls Teile der Fläche ober- und unterhalb der x-Achse liegen, das Integral für beide Teile einzeln berechnen lassen und die Beträge davon – falls ein Integral negativ war – addieren). TIPP!! Auf www.thkoehler.de/midnightblue/m_kdb.htm können Sie Funktionen eingeben (und das Intervall, in dem die x-Werte liegen sollen) und das Programm rechnet die Kurvendiskussion vor (inklusive Nullstellen, 1., 2. und 3. Ableitung, Extremwerte, Wendepunkte und -tangenten, Wertetabelle, Definitionsmenge, Asymptoten, Integrale, Flächen, Bogenlänge, Zeichnung,…). Wenn Sie bei dem folgenden Witz lachen können, haben Sie eindeutig etwas von diesem Kapitel mitbekommen: Zwei Mathematikerinnen sitzen im Restaurant und unterhalten sich. Die eine stellt im Laufe des Gesprächs fest: "Niemand kann mehr Mathematik." Ihre Kollegin widerspricht ihr und als die erste aufs Klo geht, sagt die andere zur Kellnerin: "Ich werde Sie gleich etwas fragen. Dann antworten Sie einfach: Ein Drittel x zur dritten". Als die erste Mathematikerin wieder zurück am Tisch ist, meint die Kollegin: „Ich werde dir gleich zeigen, dass du mit deinem ‚Niemand kann mehr Mathematik’ Unrecht hast“, ruft die Kellnerin an den Tisch und fragt sie: "Was ist das Integral von x2 ?" Darauf antwortet die Kellnerin: "Ein Drittel x zur dritten". Beim Weggehen dreht sie sich um und sagt „plus c.“ So und nun wird es wieder ernst. Zum Abschluss gibt es wieder eine Lernzielüberprüfung. Lernzielüberprüfung „Integralrechnung“: Sie haben für die Beispiele 3 Stunden Zeit, dürfen Taschenrechner und Formelsammlung verwenden. 1. Wie lauten die Stammfunktionen der folgenden Funktionen: 1 x² 1 f) f(x) = x x a) f(x) = 2x³ - 5 b) f(x) = d) f(x) = 5.sinx – cos x e) f(x) = e2x c) f(x) = 2. Wie groß ist das Flächenstück, das die Funktion y=x³–x²–6x mit der x-Achse begrenzt? 3. Berechnen Sie die folgenden Integrale mit Hilfe der Integrationsmethoden Substitution bzw. partielle Integration bzw. Partialbruchzerlegung: 2 x³ a) 5 x b) x.e c) x² 4 x 5 dx x 4 dx dx 5x 7 1 x ² 1 wird die Tangente t gelegt. 5 a) Das Flächenstück, das zwischen f, t und den Koordinatenachsen liegt, rotiert um die x-Achse. Berechnen Sie das Volumen des entstehenden Drehkörpers! 4. Im Punkt T(5/y1) des Graphen der Funktion f: y= b) Wenn Sie die Parabel um die y-Achse rotieren lassen, in welcher Höhe würde in diesem Gefäß 1 Liter Wasser stehen (1 Einheit = 1 cm)? VIEL ERFOLG ! ! ! Auswertung: Bsp. 1a-d 1e, f 2 3a 3b 3c 4a 4b Ges. Punkte Je 3 Je 2 12 8 6 10 10 8 70 Notenschlüssel: Ab 36 Punkten ……….. Bestanden 36 – 42 Punkte ………. Genügend 43 – 51 Punkte ………. Befriedigend 52 – 60 Punkte ………. Gut 61 – 70 Punkte ………. Sehr Gut Die Lösungen finden Sie gleich anschließend! Lösungen der Lernzielüberprüfung „Integralrechnung“: 1. Wie lauten die Stammfunktionen der folgenden Funktionen: F(x) = 2. a) f(x) = 2x³ - 5 1 2 b) f(x) = xx c) f(x) = 1 x 2 x² F(x) = x4 x4 5x 5x c 4 2 3 2 x 2 . x³ + c 3 3 2 F(x) = - x-1 = - 1 +c x d) f(x) = 5.sinx – cos x F(x) = -5.cosx – sinx + c e) f(x) = e2x F(x) = ½ . e2x + c f) f(x) = 1 x F(x) = ln x + c [s. Formelheft] 2. Wie groß ist das Flächenstück, das die Funktion y=x³–x²–6x mit der x-Achse begrenzt? Zunächst suche ich die Nullstellen x³ – x² – 6x = 0 x . (x² – x – 6) = 0 x. (x – 3) . (x + 2) = 0 N1(0/0), N2(3/0), N3(-2/0) Nun berechne ich die zwei Flächenstücke: 0 x 4 x³ x² 6. A1 = ( x ³ x ² 6 x)dx 4 3 2 2 3 x 4 x³ x² 6. A2 = ( x ³ x ² 6 x)dx 4 3 2 0 0 0 ( 2 3 0 16 16 ) 3 3 63 63 0 4 4 Die Gesamtfläche setzt sich aus A1 und A2 zusammen A = 16 63 253 3 4 12 Die Fläche beträgt ca. 21,08 AE. 3. Berechnen Sie die folgenden Integrale mit Hilfe der Integrationsmethoden Substitution bzw. partielle Integration bzw. Partialbruchzerlegung: a) 2 x³ 5 x 4 dx Einsetzen Ich substituiere 5 – x4 = t -4x³ dx = dt dx = 2 x³ 5 x 4 dx = 2 x ³ dt 1 1 1 . dt . ln t t 4 x³ 2 t 2 dt 4x ³ Nach rücksubstituieren ergibt das: 2 x³ 5 x 4 1 dx = . ln 5 x 4 + c 2 b) Bei x.e x dx wende ich die partielle Integration an f .g ' f .g f '.g Da sich x beim Ableiten „vereinfacht“ und ich die Stammfunktion von ex kenne, setze ich f=x und g= ex an x.e x dx = x.e x 1.e x dx = x.ex – ex + c c) Bei 5x 7 x² 4 x 5 dx verwende ich die Partialbruchzerlegung. Dazu muss ich den Nenner in Linearfaktoren zerlegen (indem ich die Lösungen „sehe“ oder die quadratische Gleichung löse) x² – 4x – 5 = (x – 5).(x + 1) Nun setze ich an 5x 7 A B x² 4 x 5 x 5 x 1 .(x – 5).(x + 1) 5x – 7 = A.(x + 1) + B.(x – 5) 5x – 7 = Ax + A + Bx – 5B das führt zu 2 Gleichungen I5=A+B I 5x = Ax + Bx II -7 = A – 5B Die beiden Gleichungen ergeben gelöst A = 3 und B = 2 5x 7 3 2 x² 4 x 5 dx x 5 dx x 1 dx =3.lnx-5+ 2.lnx+1+ c 1 x ² 1 wird die Tangente t gelegt. 5 a) Das Flächenstück, das zwischen f, t und den Koordinatenachsen liegt (hier gelb markiert), rotiert um die x-Achse. Berechnen Sie das Volumen des entstehenden Drehkörpers! 4. Im Punkt T(5/y1) des Graphen der Funktion f: y= Zunächst berechne ich die y-Koordinate des Punktes T, indem 1 ich x=5 in y= x ² 1 einsetze T(5/6) 5 Nun stelle ich die Tangentengleichung auf: Dazu berechne ich die Steigung (=1. Ableitung) bei x=5: f’(x) = 2 2 x k = f’(5) = .5 k = 2 5 5 Wenn ich in t: y = k.x + d einsetze 6 = 2.5 + d d=-4 t: y = 2x – 4 b Zur Berechnung des Volumens verwende ich die Formel V = . y² dx , wobei ich die a Parabel in den Grenzen von 0 bis 5 rotieren lasse und die Tangente von 2 (= Schnittpunkt der Tangente mit der x-Achse) bis 5. 5 5 . x 4 2 x² x 5 2 x³ x² Vpar = . 1 dx . 1dx . x 46, 6 5 25 5 125 15 0 0 0 5 2 VTangente = 5 . . x³ . 2 x 4 dx . 4 x ² 16 x 16dx . 4. 8 x ² 16 x (46, 6 10, 6) 36 3 2 2 2 5 5 2 . Das Gesamtvolumen ergibt sich aus V1 – V2 = 10, 6 Das Volumen beträgt ca. 10,7VE oder 33,5 VE. b) Wenn Sie die Parabel um die y-Achse rotieren lassen, in welcher Höhe würde in diesem Gefäß 1 Liter Wasser stehen (1 Einheit = 1 cm)? 1 Liter Wasser entspricht 1000cm³ - das ist das Volumen, das die um die y-Achse b rotierende Parabel fassen soll. Die zugehörige Formel lautet V = . x² dy , wobei ich a die untere Grenz kenne (a=1) und die obere suche b b ² y² 1 1000 = . 5.( y 1)dy 5 . y 5 b 1 2 1 2 2 1 b 1 1000 b ² b 5 2 2 .2 b² - 2b + (1- 400/) = 0 Das Lösen der quadratischen Gleichung ergibt b12,28cm als obere Grenze (die negative Lösung kommt nicht in Frage). Da das Gefäß erst bei 1cm Höhe beginnt 1 Liter Wasser würde in dem Gefäß ca. 11,28cm hoch stehen. Ende des Lernpfades „Integralrechnung“. http://www.2bw.eu/workroom/inhalte/mathematik.htm führt zurück auf die LernpfadÜbersicht-Seite.