Lösungen: Offenes Lernen Funktionen

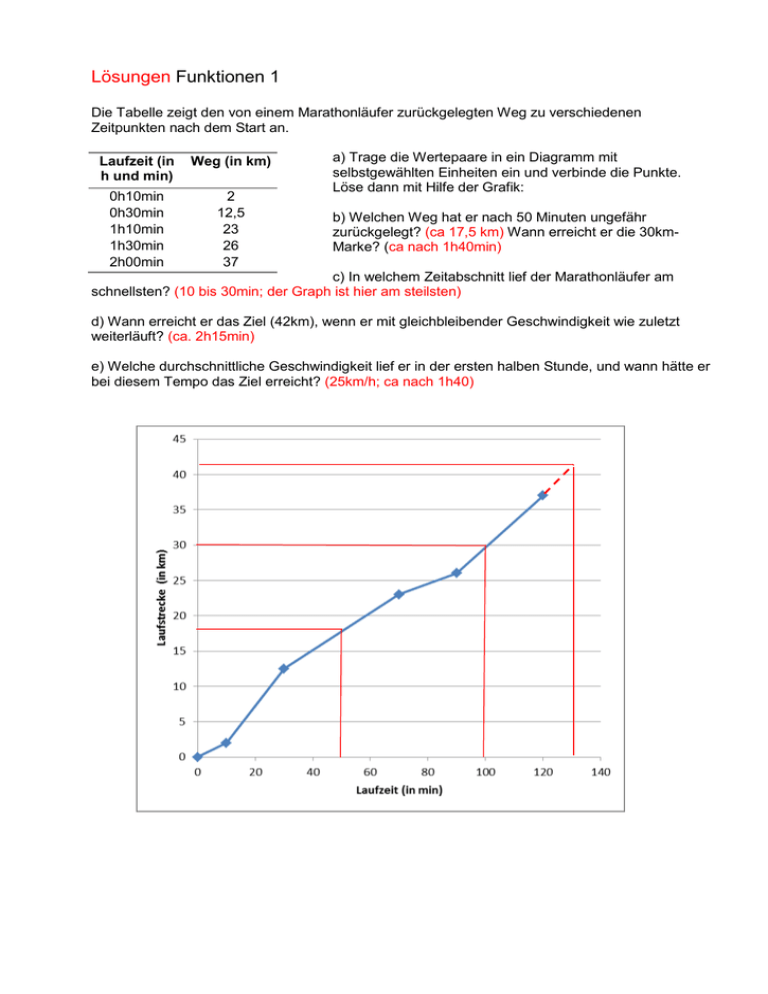
Lösungen Funktionen 1
Die Tabelle zeigt den von einem Marathonläufer zurückgelegten Weg zu verschiedenen
Zeitpunkten nach dem Start an.
Laufzeit (in
h und min)
Weg (in km)
0h10min
0h30min
1h10min
1h30min
2h00min
2
12,5
23
26
37
a) Trage die Wertepaare in ein Diagramm mit
selbstgewählten Einheiten ein und verbinde die Punkte.
Löse dann mit Hilfe der Grafik:
b) Welchen Weg hat er nach 50 Minuten ungefähr
zurückgelegt? (ca 17,5 km) Wann erreicht er die 30kmMarke? (ca nach 1h40min)
c) In welchem Zeitabschnitt lief der Marathonläufer am
schnellsten? (10 bis 30min; der Graph ist hier am steilsten)
d) Wann erreicht er das Ziel (42km), wenn er mit gleichbleibender Geschwindigkeit wie zuletzt
weiterläuft? (ca. 2h15min)
e) Welche durchschnittliche Geschwindigkeit lief er in der ersten halben Stunde, und wann hätte er
bei diesem Tempo das Ziel erreicht? (25km/h; ca nach 1h40)
Lösungen Funktionen 2
Bei einem Autoverleih kann zwischen zwei Tarifarten gewählt werden:
Tarif A: 35 € Grundgebühr pro Tag plus 1,20€ pro gefahrenem km
Tarif B: Keine Grundgebühr, 3€ pro gefahrenem km.
a) Stelle eine Wertetabelle für den Zusammenhang Weg  Kosten für 0,10,20,…50km für den
Tarif A an. Wähle zuletzt die Variable x für den Weg und berechne in der Tabelle die Kosten als
Variable y. Gib dann die Funktionsgleichung in der Art y =… und f(x) = … an.
Wegstrecke
(in km)
0
10
20
30
40
50
Preis Taxi A
(in €)
35
47
59
71
83
95
Wegstrecke
(in km)
0
10
20
30
40
50
Taxi A: f(x)=1,2.x+35
Preis Taxi A
(in €)
0
30
60
90
120
150
Taxi B: g(x)=3.x
c) Löse mit Hilfe eines Diagrammes mit beiden eingetragenen Funktonen grafisch: Bei welcher
Strecke kosten beide Tarife gleich viel? Wähle die Skala für x-Achse (Weg)und y-Achse (Kosten)
selbst!
160
140
Taxikosten (in €)
120
100
80
Preis Taxi A (in €)
60
Preis Taxi B (in €)
40
20
0
0
20
40
gefahrene Strecke (in km)
Bei ca 20km
60
Funktionen 3
Wie müssen die fehlenden Angaben (Fragezeichen) für Veränderungen im Sinne der
angegebenen Zusammenhänge lauten? (Notiere die Antwort im Sü-Heft!)
a) direkte Proportionalität:
(1)
(2)
3-facher x-Wert
8-facher x-Wert
=>
=>
3-facher y-Wert
8-facher y-Wert
2-facher x-Wert
3-facher x-Wert
=>
=>
4-facher y-Wert
9-facher y-Wert
c) indirekte Proportionalität (1)
(2)
doppelter x-Wert
ein drittel x-Wert
=>
=>
halber y-Wert
dreifacher y-Wert
d) linearer Zusammenhang
(1)
(2)
(3)
x
2
4
5
6
-3
(4)
(5)
k=2
d=1
b) quadratischer Zusammenhang
(1)
(2)
y
5
9
11
13
-5
Funktionen 4
Welche Diagramme passen zu den folgenden Texten? Gib die passende Diagrammnummer an
und welche Bedeutung dann die x-Achse und die y-Achse haben! Manchmal könnten auch
mehrere Lösungen richtig sein (Gib dann mehrere Diagrammnummern an). Antworten am
Arbeitsblatt Einkleben ins Sü-Heft!
a) Fieberkurve eines Patienten:
Diagrammnr.: 8
x-Achse: Zeit
y-Achse: Körpertemperatur
b) Ein Taxi kostet 8,- pro km , ab 20 km allerdings nur mehr 6.- pro km
Diagrammnr.: 4
x-Achse:Strecke
y-Achse:Preis
c) Ein Zug fährt von Wien nach St. Pölten , hält dort eine Stunde und fährt
dann wieder zürück nach Wien
Diagrammnr.:7
x-Achse:Zeit
y-Achse: Entfernung von Wien
d) Ein Taxi kostet 20,- Grundgebühr und 5,- pro km
Diagrammnr.:6
x-Achse:Fahrtstrecke
y-Achse: Preis
e) Ein mit konstanter Geschwindigkeit fahrendes Auto
Diagrammnr.: 9 [3]
x-Achse:Zeit
y-Achse:Geschwindigkeit [Strecke]
f) Kreisfläche in Abhängigkeit vom Radius
Diagrammnr.:1
x-Achse:Radius
y-Achse:Kreisfläche
g) Temperaturverlauf des Wetters während eines Tages
Diagrammnr.:5 [8]
x-Achse:Tageszeit
y-Achse:Temperatur
h) Ein Flugzeug beim Landeanflug
Diagrammnr.:2
x-Achse:Zeit
y-Achse:Flughöhe über dem Grund
k) Flugzeugflug von Wien nach Paris
Diagrammnr.:7
x-Achse:Zeit
y-Achse:Flughöhe
l) Taxi ohne Grundgebühr: 7,- pro km
Diagrammnr.:3
x-Achse:Strecke
y-Achse: Preis