Wiederholung, Ergänzung, Vertiefung – Analysis (1) In St. Louis

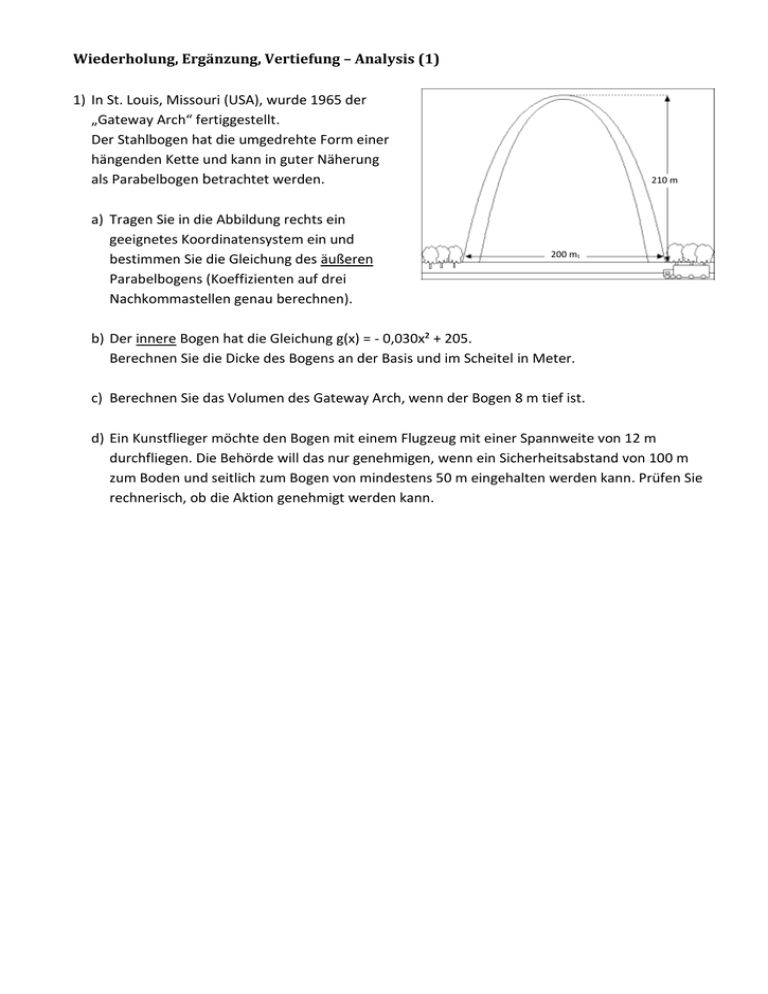
Wiederholung, Ergänzung, Vertiefung – Analysis (1)
1) In St. Louis, Missouri (USA), wurde 1965 der
„Gateway Arch“ fertiggestellt.
Der Stahlbogen hat die umgedrehte Form einer
hängenden Kette und kann in guter Näherung
als Parabelbogen betrachtet werden.
a) Tragen Sie in die Abbildung rechts ein
geeignetes Koordinatensystem ein und
bestimmen Sie die Gleichung des äußeren
Parabelbogens (Koeffizienten auf drei
Nachkommastellen genau berechnen).
210 m
200 m
b) Der innere Bogen hat die Gleichung g(x) = - 0,030x² + 205.
Berechnen Sie die Dicke des Bogens an der Basis und im Scheitel in Meter.
c) Berechnen Sie das Volumen des Gateway Arch, wenn der Bogen 8 m tief ist.
d) Ein Kunstflieger möchte den Bogen mit einem Flugzeug mit einer Spannweite von 12 m
durchfliegen. Die Behörde will das nur genehmigen, wenn ein Sicherheitsabstand von 100 m
zum Boden und seitlich zum Bogen von mindestens 50 m eingehalten werden kann. Prüfen Sie
rechnerisch, ob die Aktion genehmigt werden kann.
2) Die dargestellte Brücke führt mitten über eine 3,5 m breite Straße und hat einen parabelförmigen
Bogen. Auf der Brücke ist ein Fußweg.
5,5 m
4,5 m
4,5 m
3,5 m
6m
1m
4m
1m
a) Tragen Sie in die Darstellung oben ein geeignetes Koordinatensystem ein und bestimmen Sie die
Gleichung des Brückenbogens.
b) Bestimmen Sie die Steigung des Fußweges auf der Brücke.
c)
Für welche Durchfahrtshöhe ist die Brücke auf der 3,50 m breiten Straße maximal zulässig?
d) Berechnen Sie dazu den Inhalt der Querschnittsfläche unter dem Bogen.
e) Die Brücke ist 4 m tief. Wie viel Material (in m³) wurde bei ihrer Herstellung verbaut?
3) Die dargestellte 60 m lange waagerechte Straßenbrücke soll auf einem parabelförmigen
Brückenbogen konstruiert werden. Brückenfundament A (Anfangspunkt) liegt 14 m und
Brückenfundament E (Endpunkt) liegt 8 m unter der Fahrbahn. Der Stützpfeiler in der Mitte der
Brücke (30 m) soll 2 m lang sein.
Alle 10 m soll jeweils ein senkrechter Stützpfeiler zwischen Brückenbogen und Fahrbahn gesetzt
werden. Wie lang sind diese Stützpfeiler?
60,00 m
E
A
14,00 m tief
8,00 m tief
Lösungen:
1a)
b)
c)
x-Achse durch die Basis des Bogens, y-Achse durch den Scheitelpunkt
allgemeine Parabelgleichung: f(x) = ax² + bx + c
c = 210 , weil die y-Achse bei 210 geschnitten wird.
b = 0 , weil die Parabel achsensymmetrisch zur y-Achse liegt
(100|0) ist Punkt der Parabel, d.h. 0 = 100²a + 210  a = - 0,021
Gleichung des äußeren Parabelbogens: f(x) = - 0,021x² + 210
Dicke im Scheitel = 210 – 205 = 5 m
Nullstellen des inneren Bogens: g(x) = 0  x1 = - 82,66 oder x2 = 82,66
Dicke an der Basis = 100 – 82,66 = 17,34 m
Fläche des Bogens =
= Fläche des äußeren Bogens und der x-Achse - Fläche des inneren Bogens und der x-Achse
100
= 2 ∙ (∫0
82,66
(−0,021x 2 + 210)dx − ∫0
(−0,03x 2 + 205)dx)
= 2 ∙ ([−0,007x 3 + 210x]100
− [−0,001x 3 + 205x]82,66
) = 5405,18 m²
0
0
d)
2a)
b)
c)
d)
e)
Volumen des Bogens = Fläche  Tiefe = 5.405,18  8 = 43.241,44 m³
innere Breite des Bogens in 100 m Höhe: 100 = g(x)  x1 = - 59,16 oder x2 = 59,16,
d.h. in 100 m Höhe ist der Bogen innen 118,32 m breit.
Der Abstand des Flugzeugs ist (118,32 – 12) : 2 = 53,16 m > 50 m;
der Flug kann genehmigt werden.
x-Achse durch die Straße, y-Achse durch den Scheitel
1
m=
8
Allgemeine Parabelgleichung: f(x) = ax² + bx + c
b = 0 , weil die Parabel spiegelsymmetrisch zur y-Achse ist
c = 4,5 , weil die Parabel die y-Achse bei 4,5 schneidet
(3|0) ist Punkt der Parabel, d.h. = 3²a + 4,5  a = - 0,5
Ergebnis: f(x) = - 0,5x² + 4,5.
f(1,75) = 2,97 m, d.h. der Abstand zwischen Straße und Bogen beträgt 2,97 m.
Die maximal zulässige Durchfahrtshöhe sollte inklusive eines Sicherheitsabstands etwa 2,70 m
betragen.
Nullstellen x1 = -3 und x2 = 3. Wegen der Symmetrie ist
3
1
A = 2   ( 0,5x ²  4,5)dx  2  [ x ³  4,5x ]30  18 m²
6
0
V = 4 m  (5  8 m² - 18 m²) = 88 m³
3)
y-Achse
60,00 m
x-Achse
P3 (30|-2)
E
A
8,00 m tief
14,00 m tief
Allgemeine Funktionsgleichung: f(x) = ax² + bx + c
A(0|-14): c = - 14
P3 (30|-2): 30²a + 30b – 14 = - 2
E(60|-8): 60²a + 60b – 14 = - 8
Ergebnis: f(x) = - 0,01x² + 0,7x – 14
Aus der Funktionsgleichung ergeben sich die Längen der Stützpfeiler:
Abstand x:
10 m
20 m
40 m
50 m
Pfeilerlänge f(x):
8m
4m
2m
4m