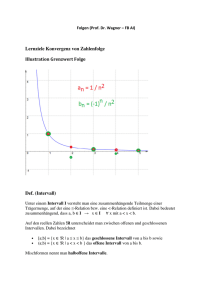
grenzwertig_01_herz

Technische Universität München
Fortbildungsveranstaltung für Lehrer
am 23. September 2008
in Garching
Ein aus der
Anschauung gewonnener
Grenzwertbegriff
Ein Unterrichtskonzept zur Einführung des Grenzwertbegriffs
in der 10. Jahrgangsstufe
des achtjährigen Gymnasiums
Andreas Herz
Allgäu-Gymnasium Kempten
[email protected]
Projektor-Folie zum Einstieg in die Grenzwert-Thematik
Arbeitsblatt zur Einführung des Grenzwertbegriffs
Übungsblatt zur Festigung des Grenzwertbegriffs
Folie zum Einstieg
Gegen welchen Wert streben die Funktionswerte der Funktion f für x
?
x
1
100
1000
2000
4000
4100
4200
4300
4400
4500
4550
...
Gegen den Wert 0,6.
Tatsächlich ?
f(x)
2,81
2,80
2,51
1,82
0,66
0,64
0,62
0,62
0,61
0,61
0,60
...
M10 - AB07
Grenzwerte von Funktionen für x 
x+4
2x
Auftrag Finde den Grenzwert der Funktion f : x
Datum

ausgefüllt
für x   .
Optimist
Skeptiker
„Der
Grenzwert
Ein Dialog zwischen einem Optimisten und einem Skeptiker
ist
0,5
______“
O:
Das ist doch klar: Für „x gegen  “ strebt die Funktion f
„Das glaub’
0,5
gegen _____
.
0,5
S:
Das glaube ich nicht! Dann müssten ja die Funktionswerte f(x)
für
steigende x-Werte dem y-Wert 0,5 beliebig nahe kommen.
_____________________________________________________
O:
Das tun sie doch auch!
S:
Das beweise mir! Ich gebe dir die Toleranz ε = 1 vor.
ich
nicht!“
Toleranz:
ε =1
Wenn deine Vermutung richtig ist, dann müsstest du mir nun einen
der Graph ab dieser
Schwellenwert k angeben können, so dass __________________
Stelle
k vollständig in dem waagrechten Schlauch um die
_____________________________________________________
Gerade
y = 0,5 mit dem „Schlauchradius“ 1 liegt.
_____________________________________________________
_____________________________________________________
Schwellenwert:
3
k = ___
O:
3
Bitte schön: k = ___
S:
Bilder können trügen. Das beweise mir rechnerisch!
O:
3 der Graph sich
Aber gerne! Ich zeige Dir, dass für x > ______________________
beweise mir
vollständig innerhalb eines um die Gerade y = 0,5 symmetrisch
______________________________________________________
durch eine
liegenden waagrechten Schlauchs der Breite 1 befindet.
______________________________________________________
Rechnung!“
Denn für x mit x > 3
f(x) - 0,5 =

gilt:
x4
x4
x
 0,5 

2x
2x
2x
2
x

x  3
2
3

1



4
2x

„Das
M10 - AB07
Grenzwerte von Funktionen für x 
x+4
2x
Auftrag Finde den Grenzwert der Funktion f : x
Datum

ausgefüllt
für x   .
Optimist
Skeptiker
„Der
Grenzwert
Ein Dialog zwischen einem Optimisten und einem Skeptiker
ist
0,5
______“
O:
Das ist doch klar: Für „x gegen  “ strebt die Funktion f
„Das glaub’
0,5
gegen _____
.
0,5
S:
Das glaube ich nicht! Dann müssten ja die Funktionswerte f(x)
für
steigende x-Werte dem y-Wert 0,5 beliebig nahe kommen.
_____________________________________________________
O:
Das tun sie doch auch!
S:
Das beweise mir! Ich gebe dir die Toleranz ε = 1 vor.
ich
nicht!“
Toleranz:
ε =1
Wenn deine Vermutung richtig ist, dann müsstest du mir nun einen
der Graph ab dieser
Schwellenwert k angeben können, so dass __________________
Stelle
k vollständig in dem waagrechten Schlauch um die
_____________________________________________________
Gerade
y = 0,5 mit dem „Schlauchradius“ 1 liegt.
_____________________________________________________
_____________________________________________________
Schwellenwert:
3
k = ___
O:
3
Bitte schön: k = ___
S:
Bilder können trügen. Das beweise mir rechnerisch!
O:
3 der Graph sich
Aber gerne! Ich zeige Dir, dass für x > ______________________
beweise mir
vollständig innerhalb eines um die Gerade y = 0,5 symmetrisch
______________________________________________________
durch eine
liegenden waagrechten Schlauchs der Breite 1 befindet.
______________________________________________________
Rechnung!“
Denn für x mit x > 3
f(x) - 0,5 =

gilt:
x4
x4
x
 0,5 

2x
2x
2x
2
x

x  3
2
3

1



4
2x

„Das
S:
 = 0,25
O:
Skeptiker
Die erste Runde geht an dich, wie sieht’s aber mit der Toleranz
aus?
10 .
Kein Problem, dann nehmen wir halt k = ___
Optimist
Toleranz:
 = 0,25
Schwellenwert:
10
k = ___
Denn für x mit x > 10 gilt:
f(x) - 0,5
x  10
2
10
 0,2  0,25 
Und was ist bei der Prüfzahl ε = 0,05 ?
O:
Dann nehmen wir halt
f(x) - 0,5
50
k = ___
O:
S:
du endlich
=
Toleranz:
 = 0,05
50 . Denn für x mit x > 50 gilt:
k = ___

2
x

x  50
2
50
 0,04  0,05 

Gibst du jetzt auf und glaubst mir, dass der Grenzwert stimmt?
Erst wenn du für jede Toleranz  (  > 0) einen Schwellenwert
______________________________________________________
angeben kannst, gebe ich auf.
______________________________________________________
auf?
Definition:

2
x
S:
Schwellenwert:
Gibst
=
______________________________________________________
Eine Funktion f besitzt für „x gegen Unendlich“ den Grenzwert a , wenn es
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
Man sagt dann: _______________________________________________________________
Und schreibt:
____________________________________
oder
Um Recht zu bekommen muss demnach der Optimist ________________________________________
alle Runden gewinnen
,
nur eine Runde für sich entscheiden muss.
während der Skeptiker _________________________________________________________________
.
O:
angeben kannst, gebe ich auf.
Um die Frage nach dem Grenzwert nun endgültig zu klären, zeige
ich dir, dass es zu jeder Prüfzahl ε > 0 einen Schwellenwert
Schwellenwert:
gibt, nämlich
2
k=___
f(x) - 0,5
S:
k
=
2
2
x

. Denn für x mit x >

2
x  
2
2

2

gilt:


Jetzt bin ich überzeugt!
__________________________________
lim f(x)= 0,5
x 
k
Toleranz:
>0
S:
 = 0,25
O:
Skeptiker
Die erste Runde geht an dich, wie sieht’s aber mit der Toleranz
aus?
10 .
Kein Problem, dann nehmen wir halt k = ___
Optimist
Toleranz:
 = 0,25
Schwellenwert:
10
k = ___
Denn für x mit x > 10 gilt:
f(x) - 0,5
x  10
2
10
 0,2  0,25 
Und was ist bei der Prüfzahl ε = 0,05 ?
O:
Dann nehmen wir halt
f(x) - 0,5
50
k = ___
O:
S:
du endlich
=
Toleranz:
 = 0,05
50 . Denn für x mit x > 50 gilt:
k = ___

2
x

x  50
2
50
 0,04  0,05 

Gibst du jetzt auf und glaubst mir, dass der Grenzwert stimmt?
Erst wenn du für jede Toleranz  (  > 0) einen Schwellenwert
______________________________________________________
angeben kannst, gebe ich auf.
______________________________________________________
auf?
Definition:

2
x
S:
Schwellenwert:
Gibst
=
______________________________________________________
Eine Funktion f besitzt für „x gegen Unendlich“ den Grenzwert a , wenn es
zu jeder noch so kleinen Toleranz  (  > 0) einen Schwellenwert k ( k  ) gibt, so dass für alle
____________________________________________________________________________
____________________________________________________________________________
x > k die Abweichung f(x)  a kleiner als  ist.
____________________________________________________________________________
f strebt (konvergiert) für x   gegen den Grenzwert a.
Man sagt dann: _______________________________________________________________
Und schreibt:
____________________________________
f(x)  a
für
x  
oder
lim f(x) = a
x 
alle Runden gewinnen
Um Recht zu bekommen muss demnach der Optimist ________________________________________
,
nur eine Runde für sich entscheiden muss.
während der Skeptiker _________________________________________________________________
.
O:
angeben kannst, gebe ich auf.
Um die Frage nach dem Grenzwert nun endgültig zu klären, zeige
ich dir, dass es zu jeder Prüfzahl ε > 0 einen Schwellenwert
Schwellenwert:
gibt, nämlich
2
k=___
f(x) - 0,5
S:
k
=
2
2
x

. Denn für x mit x >

2
x  
2
2

2

gilt:


Jetzt bin ich überzeugt!
__________________________________
lim f(x)= 0,5
x 
k
Toleranz:
>0