Laboratoriumsbericht

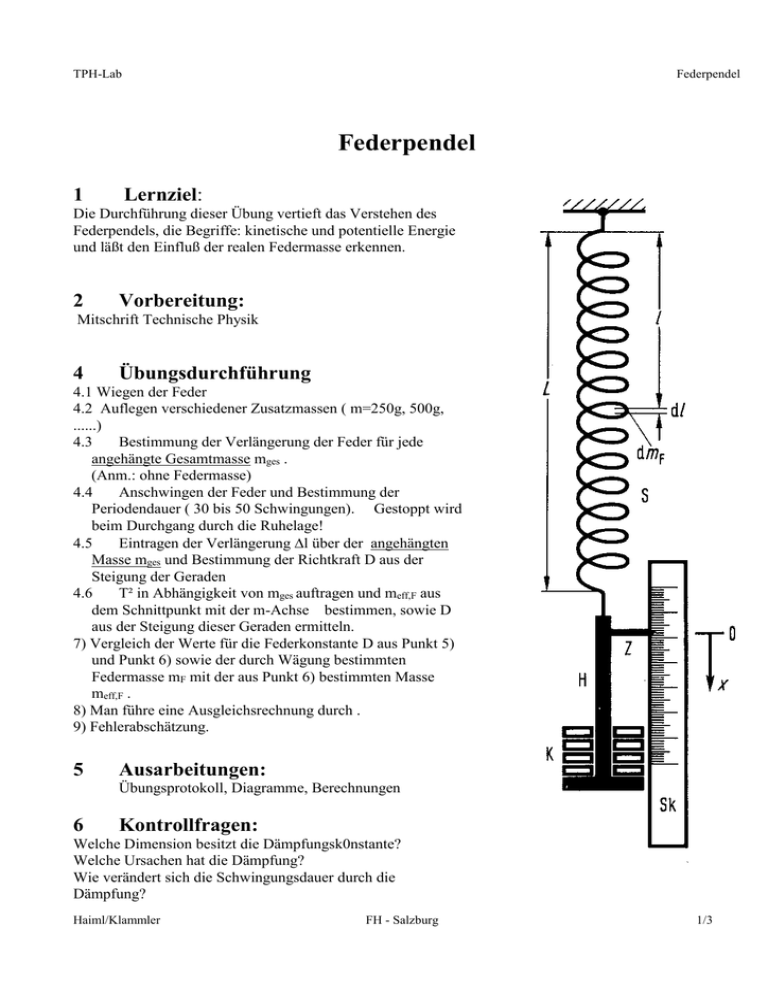
TPH-Lab
Federpendel
Federpendel
1
Lernziel:
Die Durchführung dieser Übung vertieft das Verstehen des
Federpendels, die Begriffe: kinetische und potentielle Energie
und läßt den Einfluß der realen Federmasse erkennen.
2
Vorbereitung:
Mitschrift Technische Physik
4
Übungsdurchführung
4.1 Wiegen der Feder
4.2 Auflegen verschiedener Zusatzmassen ( m=250g, 500g,
......)
4.3
Bestimmung der Verlängerung der Feder für jede
angehängte Gesamtmasse mges .
(Anm.: ohne Federmasse)
4.4
Anschwingen der Feder und Bestimmung der
Periodendauer ( 30 bis 50 Schwingungen). Gestoppt wird
beim Durchgang durch die Ruhelage!
4.5
Eintragen der Verlängerung l über der angehängten
Masse mges und Bestimmung der Richtkraft D aus der
Steigung der Geraden
4.6
T² in Abhängigkeit von mges auftragen und meff,F aus
dem Schnittpunkt mit der m-Achse bestimmen, sowie D
aus der Steigung dieser Geraden ermitteln.
7) Vergleich der Werte für die Federkonstante D aus Punkt 5)
und Punkt 6) sowie der durch Wägung bestimmten
Federmasse mF mit der aus Punkt 6) bestimmten Masse
meff,F .
8) Man führe eine Ausgleichsrechnung durch .
9) Fehlerabschätzung.
5
Ausarbeitungen:
Übungsprotokoll, Diagramme, Berechnungen
6
Kontrollfragen:
Welche Dimension besitzt die Dämpfungsk0nstante?
Welche Ursachen hat die Dämpfung?
Wie verändert sich die Schwingungsdauer durch die
Dämpfung?
Haiml/Klammler
FH - Salzburg
1/3
TPH-Lab
7
Federpendel
Anhang:
Wir betrachten zunächst ein idealisiertes Federpendel, bestehend aus einem Körper K der Masse m, der an
einer Spiralfeder S mit der Federkonstanten (Richtkraft) D aufgehängt ist. Verschiebt man K in senkrechter
Richtung um die Strecke x aus seiner Ruhelage, so übt die gespannte Feder auf K die rücktreibende Kraft F
= - D.x aus. Läßt man K los, so bewirkt F eine Beschleunigung
a = d²x/dt² in Richtung Ruhelage (x = 0), die mit der wirkenden Kraft durch F = m.a zusammenhängt, so
daß also:
F = m.a = -D.x
Damit wird die Bewegungsgleichung:
d²x/dt² + D/m . x = 0.
Dies ist die DGL einer harmonischen Schwingung. Die Schwingungsdauer dieses idealisierten Pendels ist :
m
TF0 = 2
D
Für die Feder ohne Masse (m=0) wäre demnach die Periodendauer T = 0, was aber offensichtlich nicht
richtig ist.
Zur Berücksichtigung der Federmasse geht man vom Energieerhaltungssatz aus, nachdem die Summe aus
potentieller und kinetischer Energie des Systems eine Konstante sein muß. Die potentielle Energie in der
Lage x ist:
Epot = - F dx = ½ D x²
Die kinetische Energie setzt sich zusammen aus der kinetischen Energie des Körpers K
Ekin= ½ mv²/2 = ½ m dl/L (dx/dt)²
und der kinetischen Energie der Feder. Zu deren Berechnung denkt man sich die Feder in kleine Stückchen
der Länge dl und der differentiell kleinen Masse dmF zerlegt.
Wenn die Feder homogen ist, gilt dmF = mF dl/L.
Ist der Abstand des Massenelements dmF vom Aufhängepunkt gleich l, so wird dieses Element aus der
Ruhelage um das Stück xl / L ausgelenkt, wenn der Körper um x verschoben wird. Bewegt sich also
der Körper mit der Geschwindigkeit dx/dt, so bewegt sich das Massenelement dmF mit der
Geschwindigkeit d/dt und hat dementsprechend die Energie:
Ekin,F= ½ dmF ²½ mF (dx/dt)² l²/L²
Die gesamte kinetische Energie der Feder findet man wieder durch Integration über die Energien der
differentiell kleinen Feder-Massenelemente:
l L
Ekin =

½ mF (dx/dt)² l²/L² dl/L = ½ mF (dx/dt)² /3
l0
Damit wird die Gesamtenergie des Federpendels
Eges,F = ½ (m + mF/3)(dx/dt)² + ½ D x².
Haiml/Klammler
FH - Salzburg
2/3
TPH-Lab
Federpendel
Diese Gleichung nach der Zeit differenziert ( E ist zeitlich konstant --> dE/dt =0), ergibt die
Schwingungsgleichung unter Berücksichtigung der Federmasse:
(m + mF/3) d²x/dt² + D x = 0.
Den Ausdruck mF/3 = meff,F bezeichnet man auch als effektive Federmasse.
Die Periode wird somit:
TF = 2
m  m eff,F
D
)
Trägt man T² als Funktion von m auf, so ergibt sich eine Gerade, welche die m-Achse bei
m = -mF/3 schneidet. Ihre Steigung ist gleich 4²/D und hängt somit nur von D ab.
Haiml/Klammler
FH - Salzburg
3/3