Was-Wenn-Analyse: Produktionsplanung

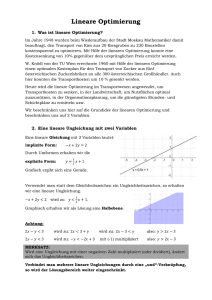
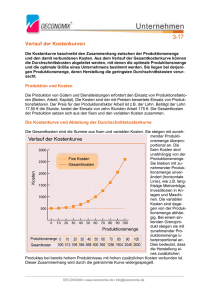
PRODUKTIONSPLANUNG – Optimierungsmodell
a) Ausgangslage
 Was soll optimiert werden?
 Zielfunktion:
Die Produktionsmengen der Produkte P, Q und R sind so
zu bestimmen, dass die Produktionskosten minimal sind.
 Was kann/muss getan werden, um die Produktion zu
optimieren?
 Restriktionen:
Die vorhanden Ressourcen sind so auf die Produkte zu
verteilen, dass einerseits der Mindestverbrauch eingehalten
wird und andererseits die Produktionskosten möglichst klein
sind.
PRODUKTIONSPLANUNG – Optimierungsmodell
a) Optimierungsmodell
unabhängige Variablen:
xP ...
xQ ...
xR ...
Produktionsmenge von P
Produktionsmenge von Q
Produktionsmenge von R
Zielfunktion:
Produktionskosten
K(xP, xR, xS) = 30 xP + 20 xQ + 10 xR = minimal
Ressourcen:
Material M
2 xP + 3 xQ + 4 xR  50
2 xP + 3 xQ + 4 xR  35
Material N
1 xP + 2 xQ + 5 xR  70
1 xP + 2 xQ + 5 xR  40
Beschränkung
Mindestverbrauch
Beschränkung
Mindestverbrauch
Nichtnegativitätsbedingungen:
xP  0, xQ  0, xR  0
PRODUKTIONSPLANUNG – Tabellenkalkulationsmodell
PRODUKTIONSPLANUNG – Excel-Solver
a)Solver-Parameter
 Zielzelle:
$D$40
 Zielwert:
Min
 veränderbare Zellen:
$B$38:$D$38
 Nebenbedingungen:
$B$38:$D$38 = Ganzzahlig
$B$38:$D$38 >= 0
$F$35 <= $G$35
$F$35 >= $E$35
$F$36 <= $G$36
$F$36 >= $E$36
b)Solver-Optionen
 Höchstzeit:
100 Sekunden
 Iterationen:
100
 Genauigkeit:
0.000001
 Toleranz:
5%
 Lineares Modell voraussetzen
 Schätzung:
linear
 Differenzen:
Vorwärts
 Suchen:
Newton
PRODUKTIONSPLANUNG.XLS – Excel-Solver
a)Optimum berechnen
 Produktionsplan:
xP = 0, xQ = 0, xR = 9
 Kostentotal:
0 · 30 + 0 · 20 + 9 · 10 = 90
 verbrauchte Ressourcen:
Material M: 36
Material N:
45
b)Lösung beurteilen
 Man kann tatsächlich kein optimaleres Ergebnis finden.
 Das Ergebnis löst die gestellte Aufgabe.
 Das Ergebnis verbraucht viel Material ohne grosse Kosten zu
verursachen. Muss beispielsweise das Lager geräumt werden, so ist das Ergebnis befriedigend.
Meist strebt eine Produktion jedoch ein möglichst hohen Gewinn an. Das Modell verfolgt offensichtlich nicht dieses Ziel.
c)Modell ändern
 Betragen die Herstellungskosten für Produkt R 20.-, so gibt
es kein eindeutiges Minimum mehr. Der Excel-Solver liefert
zwei verschiedenen Produktionspläne, die beide ein Kostentotal von 180.- liefern.:
xP = 0, xQ = 1, xR = 8
xP = 0, xQ = 0, xR = 9
 Möchte man von jedem Produkt je mindestens zwei Stück
produzieren, so ändern die Nichtnegativitätsbedingungen:
xP  2, xQ  2, xR  2.
Der Produktionsplan lautet nun:
xP = 2, xQ = 2, xR = 7
Das Kostentotal beträgt:
2 · 30 + 2 · 20 + 7 · 10 = 170
 Neue Zielfunktion Gewinn:
G(xP, xR, xS) = 15 xP + 10 xQ + 5 xR = maximal
Die Gewinne der Produkte und die neue Zielfunktion werden
in einer zusätzlichen Excel-Tabelle berechnet:
Neue Solver-Parameter:
Zielzelle:
Zielwert:
veränderbare Zellen:
Nebenbedingungen:
$D$44
Max
$B$38:$D$38
$B$38:$D$38 = Ganzzahlig
$B$38:$D$38 >= 0
$F$35 <= $G$35
$F$35 >= $E$35
$F$36 <= $G$36
$F$36 >= $E$36
Der neue Produktionsplan lautet:
xP = 15, xQ = 0, xR = 5
Minitest: Produktionsplanung
Mehrfachoperationen sind benutzerfreundlicher als
Neuberechnungen, ...
 ... weil Mehrfachoperationen Datenpaare, und nicht nur
einzelne Daten variieren.
Ein Szenario ...
 ... untersucht ein Formelergebnis, indem es einen Datensatz
mit beliebig vielen unabhängigen Variablen variiert.
Ein Optimierungsmodell ist linear, ...
 ... wenn Zielfunktion und Nebenbedingungen lineare
Gleichungen und Ungleichungen sind.
Ein Optimierungsmodell ist ganzzahlig, ...
 ... wenn die zu optimierende Grösse nur ganzzahlige Werte
annehmen darf.