13 Die Ionenbindung
Werbung

116
13 Die Ionenbindung
Diese Art der Bindung findet man zwischen Metallen und Nichtmetallen, typischerweise etwa
zwischen den Alkalimetallen und den Halogenen. Treibende Kraft ist auch hier wieder die Bildung
stabiler Edelgasschalen, die hier durch eine Elektronenübertragung vom Metall auf das Nichtmetall
erfolgt.
.
Na
.
+
Na+ Cl -
Cl
[Ne]3s1
[Ne]3s23p5
kleine
Ionisierungsenergie
große
Elektronenaffinität
[Ne] [Ar]
Durch Elektronenübertragung vom Metallatom zum Nichtmetallatom, entstehen aus Metallatomen
Kationen (positiv geladen) und aus Nichtmetallatomen Anionen (negativ geladen).
Kationen und Anionen ziehen sich aufgrund ihrer entgegengesetzten Ladung an. Die Anziehungskraft
wird durch das Coulombsche Gesetz beschrieben.
Es lautet für ein Ionenpaar in einem Medium:
F
z K e zA e
4 0 DK
r2
o
DK
r
e
zK, zA
1
Dielektrizitätskonstante des Vakuums
Dielektrizitätskonstante eines Mediums (H2O = 78,5 Luft = 1)
Abstand der Ionen
Elementarladung
Ladungszahl für Kation bzw. Anion
Die Anziehungskraft F ist proportional dem Produkt der Ionenladungen zKe und zAe.
Sie ist umgekehrt proportional dem Quadrat des Abstandes r der Ionen und der Dielektrizitätskonstanten DK des Mediums.
Die elektrostatische Anziehungskraft ist ungerichtet, das bedeutet, dass sie in allen Raumrichtungen
wirksam wird. Daher umgeben sich die positiven Na+-Ionen symmetrisch mit möglichst vielen
negativen Cl--Ionen und vice versa. Es bildet sich daher nicht eine Verbindung, die aus
Na+Cl--Ionenpaaren besteht, sondern es entsteht ein Ionenkristall, in dem die Ionen eine regelmäßige
dreidimensionale Anordnung, ein Kristallgitter (NaCl-Gitter) bilden.
Ein Ionenkristall kann nur insgesamt als „Riesenmolekül“ aufgefasst werden. Ionenverbindungen sind
daher Festkörper mit hohen Schmelzpunkten. Da in Ionenkristallen die Ionen nur wenig beweglich
sind, sind Ionenverbindungen meist schlechte Ionenleiter. Schmelzen von Ionenkristallen leiten
dagegen den elektrischen Strom, da in der Schmelze Ionen vorhanden sind, die gut beweglich sind.
117
Ausschnitt aus dem Kristallgitter von NaCl
_
: C I - Io n e n
: N a+ - Io n e n
Steinsalzkristall (NaCl), in dem sich auf einigen Cl--Gitterplätzen Elektronen befinden, die dem
Kristall eine blaue Farbe verleihen (kein Kristall hat einen völlig perfekten Aufbau):
Steinsalzkristall NaCl
118
Kationen und Anionen nähern sich im Ionenkristall nur bis zu einer bestimmten Entfernung
(Gleichgewichtsabstand, bei dem die Coulombschen Anziehungskräfte gerade gleich den
Abstoßungskräften der Elektronenhüllen sind).
Die Ionen verhalten sich in einem Ionenkristall in erster Näherung wie starre Kugeln mit einem
charakteristischen Radius (vergl. Ionenradien der Hauptgruppenelemente S. 39). Die Elektronenhüllen
der Ionen durchdringen sich nicht, die Elektronendichte sinkt zwischen den Ionen fast auf Null.
Dichteprofil der Elektronenverteilung im NaCl-Kristall. Die „Höhenlinien“ verbinden Stellen gleicher
Elektronendichte. Die Zahlen an den Höhenlinien geben die Elektronendichte im Å-2 eines Ausschnitts
der auf die (110)-Ebene projizierten Elementarzelle.
Dichteprofil der Elektronenverteilung im
NaCl-Kristall
Für die Ionenradien gelten folgende Regeln:
a) Bei den KOZ 8, 6 und 4 verhalten sich die Radien für ein und dasselbe Ion annähernd wie
1,1 : 1 : 0,8. (Mit wachsender Zahl benachbarter Ionen vergrößern sich die Abstoßungskräfte
zwischen den Elektronenhüllen der Ionen, der Gleichgewichtsabstand wächst).
b) Kationen sind kleiner als Anionen, Ausnahmen sind die großen Kationen K+, Rb+, Cs+, NH4+, Ba2+.
Sie sind größer als das kleinste Anion F- (vergl. S. 39).
c) In den Hauptgruppen des PSE nimmt der Ionenradius mit steigender Ordnungszahl zu (vergl. S. 39).
d) Bei Ionen mit gleicher Elektronenkonfiguration (= isoelektronische Ionen) nimmt der Radius mit
zunehmender Ordnungszahl ab:
O2- > F- > Na+ > Mg2+ > Al3+
e) Gibt es von einem Element mehrere positive Ionen, nimmt der Radius mit zunehmender Ladung ab
(jeweils gleiche KOZ):
Fe2+ > Fe3+
Tl+ > Tl3+
119
Wichtige ionische Strukturen, Radienquotientenregel
In Ionenkristallen treten die KOZ 2, 3, 4, 6, 8 und 12 auf.
In Anordnungen höchster Symmetrie sind die ungerichteten elektrostatischen Kräfte am stärksten und
die Abstoßungskräfte am geringsten. Die folgende Übersicht fast einige wichtige KA- (K = Kation, A
= Anion) und KA2-Strukturen (Ionengitter, Gittertypen) zusammen.
a) KA-Strukturen
KA
Gittertyp
CsCl Cäsiumchloridgitter
KOZ
(für K und A
gleich)
Gitterausschnitt
Radienquotient
rK/ rA
8
CsCl-Struktur
0,94
NaCl-Struktur
0,56
Zinkblende-Struktur
0,40
(würfelförmige
Anordnung von
8Cl- um Cs+
(schwarze
Kugeln) und von
8Cs+ um Cl-)
NaCl
Kochsalzgitter
6
(oktaedrische
Anordnung von
6Cl- um Na+
(schwarze
Kugeln) und von
6Na+ um Cl-)
ZnS
Zinkblendegitter
4
(tetraedrische
Anordnung von
4S2- um Zn2+
(schwarze
Kugeln) und von
4Zn2+ um S2-)
120
b) KA2-Strukturen
KA2
CaF2
TiO2
Gittertyp
KOZ
(für K und A
unterschiedlich)
Flussspatgitter Ca2+ (schwarze
(Fluoritgitter) Kugeln) würfelförmig
von 8F- umgeben, um
F- 4Ca2+ tetraedrisch
angeordnet
Rutilgitter
Ti4+ von 6O2- verzerrt oktaedrisch
umgeben, um O23Ti4+ nahezu trigonal
planar angeordnet
SiO2 Cristobalitgitter Si-Atome sind tetraedrisch von 4OAtomen umgeben, die
O-Atome von 2SiAtomen linear
koordiniert
Gitterausschnitt
Radienquotient
rK/ rA
Flussspatgitter
0,75
Rutilgitter
0,44
Cristobalitgitter
0,29
Die KOZ von Kationen und Anionen hängen vom Radienquotienten rK/rA ab. Sind Kationen und
Anionen gleich groß, können 12 Anionen um das Kation gepackt werden. Mit abnehmendem
Verhältnis rK/rA wird die maximal mögliche Zahl der Anionen, die mit dem Kation in Berührung
stehen, kleiner.
121
Radienquotienten und Koordinationszahl
Koordinationszahl KOZ
Koordinationspolyeder
Radienquotient
rK/rA
Gittertyp
4
Tetraeder
0,225-0,414
Zinkblende,
Cristobalit
6
Oktaeder
0,414-0,732
Natriumchlorid,
Rutil
8
Würfel
0,732-1
Caesiumchlorid,
Fluorit
Radienquotienten rK/rA einiger KA-Ionenkristalle
Caesiumchlorid-Struktur
Natriumchlorid- Struktur
Zinkblende- Struktur
rK/rA > 0,73
rK/rA = (0,41-0,73)
rK/rA = (0,22-0,41)
CsCl
CsBr
NH4Cl
TlCl
CsI
NH4Br
TlBr
0,94
0,87
0,83
0,83
0,79
0,77
0,77
BaO
KF
CsF
NaF
KCl
CaO
KBr
KI
NaH
SrS
MnO
NaCl
VO
0,97
0,96
0,78
0,77
0,76
0,71
0,71
0,64
0,66
0,61
0,59
0,56
0,56
LiF
CaS
CoO
NaBr
MgO
NiO
NaI
LiCl
MgS
LiBr
LiI
0,56
0,54
0,53
0,52
0,51
0,49
0,47
0,41
0,39
0,38
0,34
BeO
BeS
0,25
0,19
122
Radienquotienten rK/rA einiger KA2-Ionenkristalle
Fluorit-Struktur
Rutil- Struktur
Cristobalit- Struktur
rK/rA > 0,73
rK/rA = (0,41-0,73)
rK/rA = (0,22-0,41)
BaF2
PbF2
SrF2
BaCl2
CaF2
CdF2
UO2
SrCl2
1,02
0,89
0,85
0,75
0,75
0,71
0,69
0,62
MnF2
FeF2
PbO2
ZnF2
CoF2
CaCl2
MgF2
NiF2
0,62
0,59
0,56
0,56
0,56
0,55
0,54
0,52
CaBr2
SnO2
MgH2
WO2
TiO2
VO2
CrO2
MnO2
GeO2
0,51
0,49
0,47
0,46
0,44
0,42
0,39
0,38
0,38
SiO2
BeF2
0,29
0,26
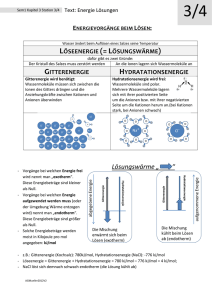
Die Bindungsenergie in Ionenkristallen (Gitterenergie HG)
Die Gitterenergie von Ionenkristallen ist die Energie, die frei wird, wenn sich weit voneinander
entfernte, im Grundzustand befindliche Kationen und Anionen einander nähern und zu einem
Ionenkristall ordnen.
Gitterenergie für KCl:
K+ (g) + Cl- (g)
KCl (s)
HG = -717 kJ/mol
Die Gitterenergie von Ionenkristallen einer bestimmten Struktur nimmt mit abnehmender Ionengröße
und zunehmender Ionenladung zu.
123
Gitterenergien HG [kJ/mol]
LiF
1037
LiCl
852
LiBr
815
LiI
761
NaF
926
NaCl
786
NaBr
752
NaI
705
KF
821
KCl
717
KBr
689
KI
649
MgO 3850
CaO 3461
SrO
3283
BaO 3114
MgS
CaS
SrS
2974
BaS
3406
3119
2832
Die Größe der Gitterenergie ist ein Ausdruck für die Stärke der Bindungen zwischen den Ionen im
Kristall. Mit wachsender Gitterenergie nehmen Schmelzpunkt, Siedepunkt und Härte zu; die
Löslichkeit der Salze nimmt ab (siehe unten). Gitterenergien können nicht experimentell bestimmt
werden. Man kann sie berechnen (z.B. Berücksichtigung der Coulombschen Wechselwirkungskräfte
zwischen den Ionen und den Abstoßungskräften zwischen den Elektronenhüllen) oder über den
sogenannten Born-Haber-Kreisprozess ermitteln. Dieser Kreisprozess basiert auf dem Satz von Hess,
wonach die Reaktionsenthalpie unabhängig davon ist, ob eine Reaktion in einem oder mehreren
Schritten abläuft; oder die Enthalpiedifferenz zwischen zwei Zuständen ist unabhängig vom Weg, auf
dem man vom Anfangs- zum Endzustand gelangt.
124
Born-Haber-Kreisprozess für die Ermittlung
der Gitterenergie von KCl
Cl(g)
K+(g)
K(g)
HDiss
K(g)
HSub
K(s)
HEA
Reaktionsweg 2
HIE
K+(g)
Cl(g)
Cl-(g)
Endzustand
Reaktionsweg 1
1
2
Cl2(g)
1
2
Cl2(g)
HG
HBild
KCl(s)
Enthalpieänderung
Reaktionsweg 1
=
-HG
Ausgangszustand
Enthalpieänderung
Reaktionsweg 2
= -HBild + HSub + HDiss + HIE + HEA
= (437
+
89
+ 122
+ 418
- 349) kJ/mol
-HG
= 717 kJ/mol
HG
= -717 kJ/mol {Umkehrung Reaktionsweg 1 = Bildung von KCl (s)
aus K+ (g) und Cl- (g)}
Der eigentliche Born-Haber-Kreisprozess {beginnt bei KCl (s) und endet bei KCl (s), was einer
Enthalpieänderung von 0 entspricht} geht von folgender Gleichung aus:
0
= -HBild + HSub + HDiss + HIE + HEA + HG
Die Gitterenergie ist auch von Bedeutung für die Löslichkeit von Salzen. Bei der Auflösung eines
Salzes muss die Gitterenergie durch einen energieliefernden Prozess aufgebracht werden. Dieser
Prozess ist bei der Lösung in Wasser die Hydratation der Ionen.
Beispiel:
Auflösung von NaCl (s) in H2O (vergl. S. 108)
HL = HH - HG
HH = Hydratationsenthalpie
125
Na+ (g) +
Cl- (g)
+ H 2O (l)
NaCl (s)
+ H 2O (l)
NaCl (s)
Na+ (aq) + Cl- (aq)
HH = - 790 kJ/mol
Na+ (g) + Cl- (g)
-HG = + 787 kJ/mol
Na+ (aq) + Cl- (aq)
HL = - 3 kJ/mol
Die Auflösung von NaCl (s) in Wasser ist ein schwach exothermer Vorgang. Es gibt aber auch
Lösungsvorgänge, die endotherm verlaufen.
Beispiel:
Auflösung von NH4Cl (s) in H2O
+ H 2O (l)
NH4Cl (s)
NH4+ (aq) + Cl- (aq)
HL = + 15,16 kJ/mol
In diesem Fall wird bei der Hydratation der Ionen weniger Wärme frei, als bei der Bildung des
Ionengitters.
HH = - 688 kJ/mol
HG = - 703,16 kJ/mol
Tatsächlich ist der Gesamtvorgang (die „Triebkraft“ zur Auflösung von NH4Cl) nicht allein eine Frage
der Enthalpie – sondern auch der Entropiebilanz. Wenn die „freie Reaktionsenthalpie“
GL = HL - TSL (T = Temperatur) negativ ist, so läuft die Auflösung in Wasser ab.
GL = HL - TSL
= + 15,16 kJ/mol – 298 K · 73,69 J/K · mol
= - 6,8 kJ/mol
2. Hauptsatz der Thermodynamik
Bei einer spontanen Zustandsänderung vergrößert sich die Entropie. Freiwillig stellt sich somit immer
nur ein Zustand mit geringerer Ordnung ein.
Die Entropie S ist ebenso wie die innere Energie U und die Enthalpie H eine Zustandsfunktion. Die
Entropie oder Unordnung eines Systems hat bei gegebenen Zustand einen definierten Wert. Einfach
ausgedrückt, mit der Zunahme der Unordnung in einem System (z.B. Zunahme der Teilchen, wie beim
Auflösen eines Ionengitters) nimmt die Entropie zu.
Die Gesamtänderung der Entropie SGes ist die Summe der Entropieänderungen des Systems S
(Reaktionsentropie) und der Umgebung SUmg.
SGes
= S + SUmg
SUmg = -
H
T
(1)
(2)
126
Die Entropieänderung der Umgebung kommt durch den Austausch von Wärme mit der Umgebung
zustande, bedingt durch die Reaktionsenthalpie H:
Substitution von (2) in(1):
SGes
=
TSGes =
S
-
H
T
S - H
Mit G = - TSGes ergibt sich die freie Reaktionsenthalpie
G
=
H - TS (Gibbs-Helmholtz-Gleichung)
Eine Reaktion läuft aus thermodynamischer Sicht (Betrachtung des Anfangs- und Endzustandes der
Reaktion) freiwillig ab, wenn die freie Reaktionsenthalpie negativ ist.
Mit der freien Reaktionsenthalpie werden zwei Faktoren berücksichtigt, die die Freiwilligkeit des
Ablaufs einer Reaktion bestimmen.
a) Bei einer Reaktion wird ein Energieminimum angestrebt.
Wenn das System Energie an die Umgebung abgibt, ist der Wert für H negativ; er trägt zu einem
negativen Wert für G bei.
b) Bei einer Reaktion wird ein Maximum an Unordnung angestrebt.
Ein positiver Wert für S, d.h. eine Zunahme der Unordnung im System, trägt wegen des Terms
- TS zu einem negativen Wert für G bei.
127
Einfluss der Vorzeichen von H und S auf den freiwilligen Ablauf einer Reaktion:
H
S
G = H - TS
-
+
-
stets freiwillig ab
(vergl. Abb 1a)
+
-
+
nicht freiwillig ab
-
-
- bei niedrigem T
freiwillig
(vergl. Abb 1b)
+ bei hohem T
nicht freiwillig
+ bei niedrigem T
nicht freiwillig
- bei hohem T
freiwillig
(vergl. Abb 2)
+
Abb.1:
+
Reaktion läuft
128
Abb. 2: