Zusammenfassung

Quantenteleportation
Tobias M. Weber
Ein Vortrag im Seminar “Moderne Experimente der Quantenoptik und Atomphysik“
im Sommersemester 06, Universität Mainz
( 21 Juni, 2006)
In der folgenden Zusammenfassung werden die theoretischen Grundzüge der Quantenteleportation, begründet in einer
Arbeit von Charles H. Bennett et al.[1] aus dem Jahr 1993, vorgestellt. Dabei handelt es sich um den Prozess der
Übertragung eines quantenmechanischen Zustandes zwischen zweier Systeme, die im Prinzip beliebig weit voneinander
entfernt sind und niemals direkt miteinander wechselwirken konnten. Des weiteren wird als erste experimentelle Realisierung
das von der Gruppe um Anton Zeilinger 1997 durchgeführte Experiment mit polarisierten Photonen im Detail besprochen,
sowie einige alternative Konzepte und deren Vorteile besprochen. Von größtem Interesse sind natürlich die konkreten
Anwendungen der Quantenteleportation, wie sie heute schon möglich und in Zukunft zu erwarten sind und zum Schluss
skizzenhaft beschrieben werden sollen.
1. Einleitung
A. Motivation
Zunächst soll hier die Idee der Quantenteleportation
in den Grundzügen beschrieben werden.
Betont werden muss hier zuallererst der stringente
Unterschied zum klassischen Begriff der
Teleportation, wie er zuerst von science fiction
Autoren kreiert wurde. In dieser naiven Vorstellung
versteht man unter der Teleportation eines Gegenstandes oder sogar Menschens die totale - materielle
- Auflösung des Objektes und die verzögerungsfreie
Reproduktion einer perfekten Kopie an einem
beliebig weit entfernten Ort. Natürlich muss ein
solcher Vorgang gegen physikalische Naturgesetze,
insbesondere die Erhaltungssätze verstoßen.
Demgegenüber stellt die Quantenteleportation einen
durchaus physikalischen Vorgang dar:
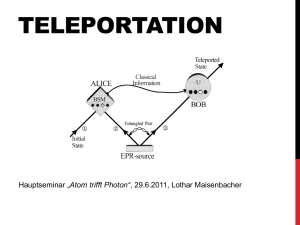
Ziel ist es, den unbekannten Quantenzustand eines
Systems von einem Sender, i. A. als „Alice“
bezeichnet, auf das entsprechende System eines
Empfängers, „Bob“, zu übertragen, d.h., es wird
keinerlei Masse transportiert und die tragende
Struktur des zu teleportierenden Zustandes liegt
schon beim Empfänger vor. Sie wurde z.B. über
einen Quantenkanal zuvor transferiert. Außerdem
wird zu Übertragung von Teilinformationen über den
zu teleportierenden Zustand stets auch ein klassischer
Informationskanal benötigt, was auch die Einhaltung
der von Einstein postulierten Lichtgeschwindigkeit
als absolute Grenze der Signalübertragung
berücksichtigt.
B. Einige Grundlagen der Quantenmechanik
Es werden nun die zum Verständnis der
Quantenteleportation benötigten Grundlagen der
Quantenmechanik beschrieben.
Im Allgemeinen wird ein System (z.B. ein Photon)
durch seinen quantenmechanischen Zustand
beschrieben. Dieser wird dargestellt als eine
Superposition von Basiszuständen, die einen
mathematisch ausreichenden Satz zur vollständigen
Beschreibung einer beliebigen Eigenschaft (z.B.
Polarisation) darstellt. Hier und im Folgenden werden
stets Eigenschaften betrachtet, die mit einer dualen
Basis beschrieben werden können. Die
entsprechenden Zustände werden dann als „qubits“
bezeichnet und können geschrieben werden als:
  a0 0  a1 1
mit der Normierungsbedingung a0 2  a1 2  1
für die Amplituden.
Von entscheidender Bedeutung für die Quantenteleportation ist das Phänomen der verschränkten
Zustände.
Dabei handelt es sich um den gemeinsamen Zustand
mehrerer (hier stets zweier) Systeme, bei dem der
Zustand des einzelnen Systems absolut unbestimmt
ist, bei beliebiger gleichartiger Messung aber die
Einzelergebnisse stets perfekt korreliert sind. Dies
bedeutet, dass sich z.B. bei der Messung der
Polarisation an zwei verschränkten Photonen stets das
selbe bzw. orthogonale Resultat ergibt, obwohl die
Photonen im Einzelnen zuvor absolut unbestimmt
waren. Ein verschränkter Zustand lässt sich somit
schreiben als
 
1
2
(0 0 1 1)
bzw.
 
1
2
(0 1 1 0)
Dabei ist keine Aussage über die Entfernung
zwischen den beiden Systemen gemacht, was
bedeutet, dass sich beide bei der Messung über eine
„spukhafte Fernwirkung“ (Einstein) über das
gleichartige bzw. orthogonale Ergebnis zu einigen
scheinen.
Hier widerspricht die Quantenmechanik in
eindeutiger Weise dem klassischen Bildes des lokalen
Realismus, nach dem eine Fernwirkung lokal durch
die Lichtgeschwindigkeit beschränkt ist und zu jedem
Messergebnis eine - vom Beobachter unabhängige –
entsprechende Wirklichkeit existiert.
2. Das Protokoll nach Bennett
A. Allgemeines Prinzip
1993 wurde zuerst von Bennett et al. ein konkreter
Vorschlag zur Realisierung der Quantenteleportation
in dem Artikel Teleporting an Unknown Quantum
State via Dual Classical and Einstein-PodolskyRosen-Channels [1] vorgeschlagen.
Ausgangspunkt ist der unbekannte Superpositionszustand einer dualen Basis eines Quantensystems 1
bzw. A beim Sender Alice:

A
 a0 0  a1 1
Den Informationsgehalt dieses Zustandes durch
einfaches Messen zu bekommen und dann zu
übermitteln ist auf Grund der quantenmechanischen
Unschärfe nicht möglich; zwar könnte man
Teilinformationen über eine der Amplituden durch
Messung eines Basiszustandes erhalten, jedoch würde
dadurch der Gesamtzustand in einen neuen Zustand
projeziert und die ursprüngliche Information wäre
unwiederbringlich verloren (projection postulate).
Stattdessen wird wie in der Überschrift
angesprochen, ein EPR-Quantenpaar, also ein
verschränktes Paar (23)

23

1
2
(0 1 1 0)
von Systemen benutzt und die Information des
Zustandes 
in einen klassischen und einen
A
quantenmechanischen Teil aufgespalten
Das Ergebnis dieser Messung wird über einen
klassischen Kanal an Bob geschickt, der mit dieser
Information in der Lage ist, sein Teilsystem des
verschränkten Paares in den ursprünglichen Zustand
zu bringen. Danach ist der Zustand bei Alice, der
durch die Bell-Zustandsmessung zerstört wurde, bei
Bob und die Teleportation abgeschlossen.
B. Quantenmechanische Rechnung
Dass die Übertragung eines Zustandes wie im obigen
Schema beschrieben auch tatsächlich die
erwünschten Resultate liefert, lässt sich durch die
quantenmechanische Rechnung nachvollziehen.
Zunächst lässt sich der gemeinsame Zustand des
Quants A von Alice und des verschränkten Paares
(23) als Produktzustand schreiben:
123  23 * A
Dies ergibt nach Einsetzen und Ausmultiplizieren:
123 
a0

2
(0
a1
2
A
(1
A
0 213 0
A
1 2 0 3)
0 2131
A
1 2 0 3)
Das gemeinsame Messen an Quant A und Quant 2
aus dem verschränkten Paar kann man nun als die
Projektion dieser Quanten in eine neue Basis von
Bell-Zuständen
12 
1
2
( 0 1 1 2  1 1 0 2)

12

1
2
( 0 1 0 2  1 1 1 2)
verstanden werden. Setzt man diese Darstellung in
den Zustand aller drei Quanten ein, so ergibt sich als
vorläufiges Resultat:
123  12 [ 12 (a0 0 3  a1 1 3 )  12 (a0 0 3  a1 1 3 )


 12
(a0 1 3  a1 0 3 )  12
(a0 1 3  a1 0 3 )]
Abb.1: Schema des Protokolls
Wie in Abb.1 dargestellt, wird ein Teil des
verschränkten Paares, das bei Alice erzeugt wurde,
über einen Quantenkanal an den Empfänger Bob
gesendet. Der andere Teil wird von Alice zu einer
gemeinsamen Messung an diesem System und ihrem
eigenen System  A , einer Bell-Zustandsmessung,
genutzt.
Dieses zunächst recht unanschaulich wirkende
Ergebnis ist nun richtig zu interpretieren:
Jedes der vier möglichen Ergebnisse der Bell

Zustandsmessung 12 und  12 erhält man mit
gleicher Wahrscheinlichkeit ¼ und total zufällig
verteilt. Kennt man dieses Ergebnis, so kann man auf
Grund der Struktur des Gesamtzustandes von (123)
mit absoluter Sicherheit sagen, in welchem Zustand
sich dann das Quant 3 bei Bob befindet! Ergibt sich
z.B. Bell-Zustand 12 , so ist Quant 3 im Zustand
(a0 0  a1 1 )
was bis auf ein Vorzeichen schon dem gewünschten
Zustand  A  a0 0  a1 1 entspricht
Die Summanden des Gesamtzustandes stellen also
jeweils zusammengehörige Ergebnisse für die
Zustände von Quanten (12) sowie Quant 3 dar.

Die Besonderheit, dass bei einem Ergebnis 12
schon der gewünschte Zustand für das Quant 3 bei
Bob vorliegt wird später im Experiment wieder eine
Rolle spielen. Liegt ein anderes Ergebnis vor, so
muss auf (3) noch eine Operation angewendet
werden, um wieder Zustand  A zu erhalten.
Dabei handelt es sich jeweils um eine Kombination
aus einem bit-flip 0  1 und dem Erzeugen
eines relativen Minuszeichens zwischen beiden
Anteilen der Superposition. So wird z.B. der
Zustand (a0 1  a1 0 ) durch diese beiden
3
3
Operationen gemeinsam wieder in den
gewünschten Zustand (a0 0 3  a1 1 3 ) gebracht.
Die Operationen lassen sich darstellen durch die
bekannten Pauli-Spinmatrizen
 { 2 ,  x ,  y ,  z } ,
sodass sich letztendlich ergibt:
Wir haben damit einen Widerspruch erzeugt und
die Annahme widerlegt!
3. Experiment nach Zeilinger
Die erste experimentelle Realisierung einer
Quantenteleportation gelang im Jahr 1997 Anton
Zeilinger et al. in Insbruck. Durch die
Ausschöpfung aller zu dieser Zeit verfügbaren
Methoden zur Erzeugung verschränkter Quanten
und quantenoptischer Manipulationen, wurde eine
Umsetzung mit Photonen erreicht.
Grundlage und damit auch quantenmechanische
Basis der betrachteten Zustände war die
Polarisation dieser Photonen und deren
Manipulation durch optische Fasern, Spiegel und
Kristalle.
Im groben Aufbau verfolgt das setup genau das
Protokoll von Bennett:.
 3  A
C. Das ‚no-cloning’-Theorem
Bei der Bell-Zustandsmessung wird der
ursprüngliche Zustand bei Quant 1 von Alice
zerstört, was die Teleportation im eigentlichen
Sinne erst perfekt macht. Dieser Umstand wird
jedoch auch schon durch die Quantenmechanik
selbst in Form des ‚no-cloning’-Theorems
gefordert:
„Ein unbekannter Quantenzustand kann nicht
perfekt kopiert werden“
D
Dass dieser Grundsatz gelten muss, lässt sich durch
einfache Überlegungen zeigen:
Abb.2: Schematischer Aufbau
Annahme: es gibt eine unitäre Zeitentwicklung, die
mit einem Hilfszustand einen Zustand
genau kopiert, also:
 h   
Wendet man diese Entwicklung auf die
Basiszustände einer dualen Basis an, so ergibt sich
damit:
0 h  0 0
1 h  1 1
Mit diesen Relationen lässt sich leicht die Wirkung
auf einen Superpositionszustand    0   1
berechnen:
( 0   1 ) h   0 0   1 1   
Man sieht sofort, dass das Resultat nicht dem
gewünschten Verdoppeln des Ursprungszustandes
entspricht.
Durch einen gepulsten Laserstrahl und einen
nichtlinearen Bariumborat-Kristall wird ein in der
Polarisation verschränktes Photonenpaar
23 
1
2
(H
2
V
3
V
2
H 3)
erzeugt, mit der Basis { H , V } für horizontal
und vertikal polarisierte Photonen. Eines (3) wird
auf direktem Weg (Strahl) zu Bob geschickt und
eines (2) zu Alice, die in diesem Schema die BellZustandsmessung vornimmt. Danach wird der
Pumpstrahl reflektiert und erzeugt in anderer
Richtung ein weiteres Photonenpaar, wobei ein
Photon (4) später zur Triggerung genutzt wird und
das andere (1) durch eine Polarisatoranordnung in
den gewünschten, zu teleportierenden Zustand

A
 a0 H  a1 V
gebracht wird. Hier ist der Zustand durch
Kenntnisse über die Polarisatoren zwecks
Überprüfung der Teleportation bekannt und
eindeutig bestimmt.
Mittels eines halbdurchlässigen Spiegels als
Strahlteiler (BS) wird nun die BellZustandsmessung an den ununterscheidbaren
Photonen 1 und 2 vorgenommen und das Ergebnis
durch Detektoren an den beiden Ausgängen
festgehalten.
Zum Schluss kann Bob durch einen polarisierenden
Strahlteiler mit den dem gewählten Anfangszustand
entsprechenden Ausgängen den Zustand seines
Photons bestimmen und die Teleportation
verifizieren.
Falschfarbenaufnahme
A. Die Photonenpaarquelle
Das Paar von Photonen im benötigten
polarisationsverschräktem Zustand wird erzeugt
durch einen Pulslaserstrahl im UV-Bereich, der
Lichtpulse der Länge 200fs erzeugt. Auf einen
nichtlinearen β-BariumboratKristall (BBO) gerichtet wird in diesem durch den
Prozess der spontanen parametrischen Fluoreszens
vom Typ II ein einfallendes Photon in zwei
polarisations-verschränkte Photonen aufgespalten:
Durch Herausfiltern bzw. –blenden aller übrigen
Bestandteile erhält man mit den Photonenpaaren
auf den so entstehenden Strahlen genau den
gewünschten verschränkten Zustand, denn von zwei
durch die Pulsdauer umgrenzten, gleichzeitig
austretenden Photonen ist mit Sicherheit eines
horizontal und eines vertikal polarisiert. Es ist aber
absolut unentscheidbar, welches welches der beiden
ist! Wir erhalten also tatsächlich zwei Photonen im
gewünschten Zustand
23 
1
2
(H
2
V
3
V
2
H 3)
B. Die Bell-Zustandsmessung
Abb.3: Prinzip der parametische. Fluoreszens
Diese treten dann spektral verteilt aus dem Kristall
aus, jedoch werden Photonen zu fester Frequenz auf
zwei Kegelmänteln emittiert. Dabei kreuzen sich
der obere mit nur horizontal polarisierten Photonen
und der untere mit den vertikal polarisierten auf
genau zwei Geraden:
Im folgenden Verlauf des Experimentes wird auf
die Identifizierung aller 4 möglichen Bell-Zustände,
deren Übermittlung mindestens einen klassischen
2-bit-Kanal bedingen würde, verzichtet. Stattdessen

wird nur der Fall mit dem Ergebnis 12
betrachtet, also das Viertel aller Fälle, in dem sich
das Photon 3 von Bob schon im richtigen
 A befindet.
Anfangszustand
Durch die beiden Detektoren ist dieser Fall
eindeutig identifizierbar. Denn:
Sprechen beide Detektoren gleichzeitig an, so
befinden sich Quant 1 und 2 im Zustand 12
Diese Aussage soll im Folgenden argumentativ
begründet werden.
Treffen auf die beiden Eingänge des Strahlteilers
zwei beliebige Photonen, so gibt es vier mögliche
Endsituationen:
d.h., entweder wird ein Photon transmittiert und das
andere reflektiert oder umgekehrt, was uns hier
beides nicht interessiert, oder beide Photonen
werden gleichzeitig transmittiert oder beide
emittiert. Die letzten beiden Fälle würden dann
jeweils zu gleichzeitigem Ansprechen der
Detektoren führen. Dieses Resultat würde also
quantenmechanisch einer Superposition der beiden
Möglichkeiten entsprechen. Wie beim
Doppelspaltexperiment, bei dem es ja auch zwei
Möglichkeiten mit gleichem Ergebnis gibt, treten
auch hier Interferenzerscheinungen auf. Dabei
entspricht der dritte Fall der Transmission beider
Photonen der destruktiven Interferenz, sodass nur
noch der letzte Fall zum Auslösen beider
Detektoren führen kann. Dies ist genau der Zustand
Dieses Resultat lässt sich auch durch die
quantenmechanische Rechnung explizit erhalten.
Zunächst werden die ein- und auslaufenden
Photonen durch die entsprechenden Erzeugungsbzw. Vernichtungsoperatoren dargestellt, wie in
Abb.4 gezeigt.
^
^
^
bH , bV
^
^
^
aH , aV
^
d H , dV
^
cH , cV
Abb.4: Vorgänge am Strahlteiler
Nun lassen sich die interessanten Zustände


12

1
2
(H 1V
2
V
1
H 2)
darstellen als Wirkungen der Erzeugungsoperatoren
auf den Vakuumzustand:
12 
1
2
(bH aV 0  bV a H 0 )
Des weiteren gelten die grundlegenden
quantenmechanischen Relationen
bH 
bV 
aH 
aV 
1
2
1
2
1
2
1
2
(d H  ic H )
(dV  icV )
(cH  id H )
(cV  idV )
Sie spiegeln die Vorgänge am Strahlteiler wider
(Reflektion →Faktor i ). Setzt man diese in die
obigen Zustände ein, so ergibt sich als
Endzustände:
 12  12 (2ic H cV  2id V d H ) 0
1
2
 12 
1
2
(2d H cV  2c H d V ) 0
1
2
Dies entspricht genau der oben geschilderten
Situation, dass Zustand 12 nicht zu einem
Photon in jedem Ausgang führen kann.
C. Durchführung und Ergebnisse
Zur Auswertung der Quantenteleportation werden
verschiedene Anfangszustände erzeugt und bei
gewünschtem Ergebnis der Bell-Zustandsmessung
die Korrektheit des Zustandes von Photon 3 bei
Bob überprüft. War der zu teleportierende Zustand
z.B. ein um +45° polarisiertes Photon, so benutzt
Bob einen polarisierenden Strahlteiler mit einem
Detektor d1 am -45°-Ausgang und einem Detektor
d2 am +45°-Ausgang. Erfolgreiche Teleportation
zeigt sich dann in einer Koinzidenzmessung
entsprechender in Abb.2 beschrifteter Detektoren.
Sie ist genau dann gewährleistet, wenn die
Detektoren der Bell-Zustandsmessung f1 und f2,
sowie d2 bei Bob und Detektor D für das bis jetzt
noch nicht beachtete zweite Photon aus dem als
zweites erzeugten Photonenpaar, gleichzeitig
ansprechen: (f1,f2,d2,D).
Die Überprüfung dieses Photons, die gleichzeitig
sicherstellt, dass überhaupt ein Photon im Zustand
 Aerzeugt wurde, ist wichtig, um sog.
Falschereignisse
auszuschließen. Mit gleicher
Wahrscheinlichkeit, wie die beiden gewünschten
Photonenpaare im BBO erzeugt werden, können
nämlich auch zwei Paare in die gleiche Richtung
des Pumplasers (nach rechts) erzeugt werden, was,
wie man sich leicht klar macht, stets zum
gleichzeitigen Auslösen der beiden Bell-Detektoren
f1 und f2 führt, obwohl gar kein Photon A erzeugt
wurde. Unter Berücksichtigung dieses Effektes lässt
sich nun die Teleportation überprüfen, indem man
den Reflektionsspiegel des Pumplasers langsam
verfährt und somit den Unterschied zwischen den
Ankunftszeiten von Photon 1 und 2 am Strahlteiler
der Bell-Messung verändert. Denn natürlich kann
diese nur korrekt stattfinden, wenn beide Photonen
miteinander interferieren, was gleichzeitiges
Ankommen voraussetzt. Um auch bei richtiger
Einstellung des Reflektionsspiegels sicherzustellen,
dass beide Photonen in ihrer Ankunftszeit
ununterscheidbar sind, werden sie zuvor durch
einen Bandbreitenfilter ( 788nm bei 4nm Breite)
geschickt, wodurch ein Bereich aus dem
einfallenden Spektrum geschnitten wird, was in der
Fouriertransformation einem breiteren Zeitfenster
für beide Photonen von 520fs entspricht. Dieses ist
größer, als die vom Pulslaser erzeugte Breite von
200fs.
Nachweis der Teleportation ist also das Messen der
Koinzidenz (D,f1,f2,d2) bei gleichzeitiger
Abwesenheit der Koinzidenz (D,f1,f2,d1).
Man erhält also als theoretische Voraussage für
eine ideale Teleportation das in Abb.5 gezeigte
Verhalten.
Abb.6: 3-fach-Koinzidenz und Rausrechnen
der „Falschereignisse“ von (68±1)%
Abb.5: theoretische Voraussage
Dies bedeutet, dass außerhalb des Teleportationsbereiches (grau unterlegt) beide Detektoren bei Bob
mit gleicher Wahrscheinlichkeit ansprechen, da sich
bei im Rahmen der Detektorgenauigkeit
unabhängig einfallenden Photonen am Strahlteiler
der Bell-Messung eine 50%-Wahrscheinlichkeit für
die Koinzidenz (f1f2) ergibt, die auf d1 und d2
gleich verteilt wird. Findet Teleportation statt, so
sollte die Rate bei dem zum teleportierenden
Zustand orthogonalem Ausgang auf Null fallen
(dip), wohingegen die Rate beim entsprechend
richtigen Ausgang gleich bleibt, da ja nur noch in ¼
aller Fälle Koinzidenz (f1f2) auftritt.
Das Experiment wurde von Zeilinger et al. sowohl
für die Basiszustände Polarosation 0° und 90° als
auch für ±45° und zirkular polarisierte Photonen
ausgewertet und es ergaben sich die in Abb.6
gezeigten Ergebnisse, die im Rahmen der
Genauigkeiten des Aufbaus mit der Theorie
eindeutig übereinstimmen.
Für 45°- und 90°-polarisierte Photonen ergab sich
dabei mit Vierfachkoinzidenz-Messung eine über
alles gemittelte Sichtbarkeit von ( 70 ± 3 )%
(prozentuale Abweichung vom idealen
theoretischen dip-Verhalten). Dieser Wert
übersteigt deutlich eine zufällige Übereinstimmung
von 50% sowie auch die maximal erreichbare
visibility ohne das Benutzen verschränkter
Zustände von 2/3, wie in [11] errechnet.
4. Alternative Experimente
A. Der nächste Schritt
Im Jahr 2004 ging die Gruppe um Anton Zeilinger
den entscheidenden Schritt in Richtung praktische
Anwendung. Allen Umwelteinflüssen ausgesetzt
wurde diesmal eine Teleportation über eine
Entfernung von 600m quer über die Donau in Wien
realisiert ([3]). Dabei wurden wiederum polarisierte
Photonen benutzt, deren Quantenzustand in einer
optischen Faser von insgesamt 800m Länge,
unterhalb der Donau verlegt, als Quantenkanal
sowie mittels eines Funkkontaktes als klassischem
Kanal teleportiert wurde.
Da der Aufbau (Abb.7) dem obigen in groben
Zügen entspricht, sollen hier nur einige
Besonderheiten besprochen werden.
Abb.7: realistische Teleportation
Zunächst wurden alle Photonen wie bekannt
erzeugt und manipuliert, allerdings ermöglichte der
komplexere Aufbau mit vier verschalteten
Detektoren an zwei Strahlteilern für die BellZustandsmessung die Unterscheidung zwischen

zwei Bell-Zuständen 12 (2 Detektoren des

selben BS ) und 12 (2 orthog. Detektoren
unterschiedlicher BS), was die Effizienz des
Experimentes verdoppelte.
Das Verhalten lässt sich wie oben durch eine
quantenmechanische Rechnung nachvollziehen.
Durch diesen Unterschied muss allerdings auch
Bob von dem Messergebnis erfahren, bevor bei ihm
das Photon 3 ankommt (active feed forward), um
vor der Analyse dessen Zustandes eine eventuell
nötige Operation am Zustand durchführen zu
können. Diese Operation besteht aus dem Erzeugen
eines relativen Minuszeichens zwischen beiden
Amplituden, was durch einen elektro-optischen
Modulator realisiert wird. Bei bedarf wird an diesen
eine Spannung von 3,7kV angelegt, wodurch der
optische Weg einer Komponente des einlaufenden
Superpositionszustandes (z.B. H-Komponente)
geeignet verlängert wird.
Um ein rechtzeitiges Erreichen der klassischen
Information zu gewährleisten wird einerseits die in
einer optischen Faser zu 2/3c verminderte
Ausbreitungsgeschwindigkeit des Photons 3
ausgenutzt und der Quantenkanal um 200
zusätzliche Meter künstlich verlängert. Dies ergibt
einen Vorsprung von 1,5µs, was der schnellen
Elektronik zum eventuellen Eingreifen ausreicht.
Auch hier wurden verschiedene Zustände
teleportiert und es ergab sich trotz einer
prozentualen Unsicherheit in der Polarisation von
±10% durch die lange optische Faser ein
prozentualer Anteil korrekter Teleportationen, auch
Fidelity
F :  A Out A dA
genannt, von 0,84 bis 0,90!
B. Time bins
Ein in [4],[5] beschriebenes Experiment zur
Quantenteleportation verwendet Energie-Zeitverschränkte Photonen.
Hier wird das Protokoll von Bennett (Abb.1) im
Wesentlichen genau analog umgesetzt, allerdings
liegt hier eine ganz andere, für Störungen weniger
anfällige Eigenschaft der benutzten Photonen zu
Grunde.
Der schematische Aufbau ist in Abb.8 gezeigt. Der
Strahl des Pumplasers wird zunächst aufgeteilt und
jeweils in ein unbalanciertes Michelson- bzw.
Faser-Interferometer geleitet durch einen
Strahlteiler bzw. Faserkoppler wird ein
einlaufendes Photon mit gleicher
Wahrscheinlichkeit durch eines der beiden Arme
geleitet.
Abb.8: time bins
Im Ausgang ergibt sich dadurch ein Superpositionszustand
  c0 long  c1ei short
Durch einen erzeugten Gangunterschied von 1,5ns,
der viel größer ist als die erzeugte Pulsbreite 150fs
ergibt sich eine Überlagerung von einem Puls, der
zur Zeit  s ausläuft und einem zur späteren
Zeit  l , da ununterscheidbar ist, durch welchen
Arm ein einzelnes Photon im Ausgang gelaufen ist.
Trifft danach dieser output wieder auf einen
nichtlinearen Kristall, so ergibt sich entsprechend
der verschränkte Zustand
 
1
2
( short
C
short
B
 ei long
C
long B )
Hier sehen wir eine andere Art der Verschränkung
bei der beide Photonen jeweils im gleichen Zustand
sind, was durch den gewählten Aufbau ja auch
zwingend logisch ist.
Nach der Erzeugung des verschränkten Zustandes
können zudem die beiden Photonen nach ihren
Wellenlängen voneinander getrennt und zur BellMessung bzw. zu Bob geschickt werden.
Auch hier wurde die Teleportation mit VierfachKoinzidenz gemessen, was dann einen
Zeitunterschied im Ansprechen der beiden BellDetektoren C1,C2 entspricht, die gleich der durch
den Gangunterschied erzeugten Differenz von
 l -  s ist.
Alice kann hier über die Wahl des Faserkopplers
(Verhältnis der Amplituden) und einen zusätzlich
integrierten Phasenschieber (relatives Vorzeichen)
beliebige Superpositionszustände erzeugen.
Auch hier wurden verschiedenste Zustände
teleportiert und auf Grund der geringeren
Störanfälligkeit von Laufzeiten gegenüber der
Polarisation eine über alle Ergebnisse gemittelte
Güte von
( 81,2 ± 2,5 )% erzielt.
Dabei lässt sich hier eine korrekte Teleportation
durch Übereinstimmung des von Alice gewählten
Phasenfaktors α mit dem von Bobs
Analyseinterferometers β verifizieren:
C. Weitere Konzepte im Überblick
i) Eine andere Methode ist das Teleportieren von
Quantenzuständen in Paulfallen lokalisierter Ionen.
wie in [9],[10] beschrieben. Dabei werden die
Ionen mit einer Serie von externen Laserpulsen
manipuliert. Da die Fallen in der Regel dicht
nebeneinander liegen (µm), ist die erreichte
Entfernung uninteressant. Allerdings sind Ionen in
diesem Fall zu 100% detektierbar, was das
Detektionsschlupfloch in der Argumentation des
lokalen Realismus schließt (siehe [7])
ii) Auch das Teleportieren kontinuierlicher
Variablen ist erwünscht und wurde erstmals von
Furusawa et al. 1998 theoretisch von Bowen et al.
2003 im Experiment realisiert mit
Amplitudenquadraten von Lichtfeldern
iii) Betrachtet man ein Lichtfeld als Überlagerung
unendlich vieler Schwingungen (FourierEntwicklung), so hat dieses Lichtfeld in der
quantenmechanischen Betrachtung in den
Raumrichtungen jeder Mode eine Unsicherheit, ein
Rauschen auf Grund der Unschärferelation. Das
Rauschen in einer Richtung kann nun zuungunsten
einer anderen unterdrückt werden. Die so
resultierenden rauschungsarmen Komponenten
können dann zu sehr präzisen Messungen
(Abstände bei Gravitationswellendetektion) benutzt
werden. Auch eine solche „Gequetschtheit“ einer
Komponente wurde erfolgreich von einem
Lichtstrahl zum anderen quantenteleportiert.
5. Anwendungen
A. Entanglement swapping
Eine der für die Zukunft von Quantencomputern
und weltweiter Quantenkanalvernetzung
bedeutendsten Anwendungen ist das sog.
‚entanglement swapping’.
Die Grundidee ist hierbei die Überlegung, was
passiert, wenn statt eines unabhängigen Zustandes
ein Zustand teleportiert wird, der seinerseits
verschränkt ist (siehe Abb.9).
BZM
Y
X
A
B
EPR
EPR
Abb.9: entanglement swapping
Dagegen spricht zunächst nichts, da die
Quantenteleportation eine lineare Operation ist.
Hier wird der Zustand X über das verschränkte Paar
(AB) auf B teleportiert. Da X aber selbst mit Y
verschränkt ist, wird genauso Zustand A auf Y
teleportiert, was im Endeffekt folgendes Resultat
hat:
Quant X und A wurden durch die BellZustandsmessung jeweils vernichtet. Jetzt befinden
sich jedoch ihrerseits Quant Y und B auf Grund der
wechselseitigen Teleportation in einem
verschränkten Zustand. Dies kann man sich leicht
über die Definition der Verschränkung als perfekte
Korrelation von Messergebnissen klar machen.
Die entstandene Situation ist dabei äußerst
bemerkenswert. Zwei Quanten, Y und B, die
niemals direkt miteinander wechselwirkten,
sozusagen keinerlei gemeinsame Vergangenheit
haben, befinden sich nach dem entanglement
swapping in einem maximal verschränkten
Zustand!
Schaltet man also mehrere der im obigen Schema
skizzierten Aufbauten hintereinander, so lässt sich
dadurch die Verschränkung über eine beliebige
Distanz aufrecht erhalten und man bekommt eine
Quantenleitung für verschränkte Zustände.
Dies würde in Zukunft die einfache Verknüpfung
von, und den Datenaustausch zwischen
Quantencomputern ermöglichen.
Eine zur Anschauung des Charakters der
Quantenmechanik interessante Fragestellung ist,
welche Ergebnisse zu erwarten sind, wenn die
Zustände Y und B vor der Bell-Messung an X und
A bestimmt würden. Sicherlich wären zunächst die
jeweiligen Teilergebnisse Für beide Zustände
vollkommen unkorreliert. Erst durch hinzuziehen
der Ergebnisliste der späteren Bell-Messung könnte
man die ursprüngliche Liste in 4, den möglichen
Bell-Zuständen entsprechenden, Teillisten zerlegen
und würde dort dann plötzlich wieder perfekte
Korrelation feststellen!
Das entanglement swapping wurde 1998 von
Weinfurter et al. im Experiment realisiert.
B. Dense coding
Eine weitere interessante Anwendung der Quantenteleportation ist das Datenkomprimieren von 2 bit
in nur einem übermittelten Quant:
2 bit
Alice
2 bit
Bob
Abb.10: dense coding
Alice und Bob erhalten jeweils ein Quant eines
verschränkten Paares. Alice kann nun ihr Quant
manipulieren und es an Bob schicken. Obwohl sie
dabei nur ein Teilchen übermittelt, kann sie
dennoch 2 bit an Information übertragen. Durch
ihre Manipulation bestimmt sie nämlich, welchen
der 4 möglichen Bell-Zustände Bob bei einer BellZustandsmessung an beiden Teilchen erhalten wird!
Gegenüber dem üblichen Informationsgehalt pro
Quant (1 bit, z.B. H- oder V-polarisiert) hat sich die
übermittelte Kapazität also verdoppelt.
6. Schlussbetrachtung
Besonders in der Betrachtung des Phänomens der
verschränkten Zustände und deren Direkter
Anwendung wie dem entanglement swapping liegt
der Schlüssel zu neuen Erkenntnissen über die
Struktur von Zeit und Raum durch die
Quantenmechanik. Besonders auch in der
Quantenkryptographie wird die
Quantenteleportation als Möglichkeit der
„abhörsicheren“ Datenübermittlung eine tragende
Rolle spielen.
Natürlich konnte in diesem Rahmen nicht auf das
ganze Spektrum des Themengebietes eingegangen
werden. Schon bis heute sind z.B. die Teleportation
von Zuständen ganzer Ionenensembles ([8]) oder
die Erzeugung verschränkter Zustände zwischen
mehr als drei Quanten realisiert worden. Auch das
Bestimmen aller 4 Bell-Zustände in der BellZustandsmessung ist Dank ausgefeilter
quantenoptischer Techniken heute möglich.
Von der Quantenteleportation zu erwarten ist in
einiger Zukunft die immer weitere Ausdehnung der
überbrückbaren Distanzen bis hin zur
Quantenkommunikation zwischen Erde und Orbit
und die Teleportation immer komplexerer
verschränkter Quantensysteme bis in die Bereiche
der Makro-Welt.
Danksagung
Ganz herzlich bedanken möchte ich mich bei Herrn
Herwig Ott für die Unterstützung in der
Vorbereitung meines Vortrages sowie der ständigen
Bereitschaft, über auftretende Probleme, wenn
nötig auch mehrmals, ausgiebig zu diskutieren.
In dieser kurzen Zusammenfassung über das
Verfahren der Quantenteleportation sind die
grundlegenden theoretischen und experimentellen
Möglichkeiten, ihren Ursprüngen und
Anwendungen aufgezeigt worden.
[1] „Teleporting an Unknown Quantum State via
Dual Classical and Einstein-Podolsky-Rosen
Channels“,
Charles H.Bennett et al.
Physikal Review Letters 70, No.13 (1993)
[4] „Long-distance teleportation of qubits at
telecommunication wavelengths“,
I.Marcikic,H.deRiedmatten,W.Tittel,
H.Zbinden,N.Gisin
Nature 421, 509 (2003)
[2] „Experimental quantum teleportation“,
A. Zeilinger et al.
Nature 390, 575 (1997)
[5] „Pulsed Energie-Time Entangled Twin-Photon
Source for Quantum Communication“;
J. Brendel,N.Gisin,W.Tittel,H.Zbinden
Physikal Review Letters 82, No.12 (1999)
[3] „Quantum teleportation across the Danube“,
A.Zeilinger et al.
Nature 430, 849 (2004)
[6] Physik Journal, November 2005
[7] „Einsteins Spuk“, Anton Zeilinger;
C.Bertelsmann Verlag 2005
[8] „Teleportation of atomic ensemble quantum
states“; Dantan et al. Feb. 2006
[9] „Deterministic quantum teleportation with
atoms“; M.Riebe, H.Häffner et al.
Nature 429, 734 (2004)
[10] „Deterministic quantum teleportation of
atomic qubits“; M.D. Barrett et al.
Nature 429, 737 (2004)
[11] “Optimal Extraction of Information from
Finite Quantum Ensembles”;
S.Massar and S. Popescu
Physikal Review Letters 74, No. 8 (1995)