Vortrag - QUANTUM

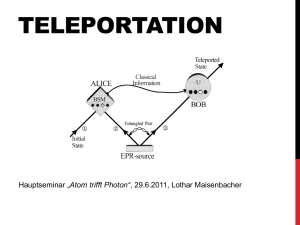
Quantenteleportation
Vortrag zum Seminar
„Moderne Experimente der Quantenoptik und Atomphysik“
von
Tobias M. Weber
Inhaltsübersicht
•
•
•
•
•
•
Einleitung
Theorie: Protokoll nach Bennett et al.
Experiment: Zeilinger et al.
Varianten
Anwendungen
Ausblick
Was ist Quantenteleportation, was nicht?
● keine Realisierung der klass. Vorstellung
von Teleportation (science fiction), bei der
Masse (Person!) über große Strecken
instantan bewegt wird
● Übertragung des Zustandes eines
Quantensystems auf ein anderes mittels eines
klass.(z.B.Funk-) und eines Quantenkanals
(tragende Struktur also schon vor Ort)
Einhalten aller physikal. Gesetze, insbesondere Einsteins
Postulat der Lichtgeschwindigkeit als absolute Grenze bei
Signalübertragung
Wiederholung
● q.m.
Zustand als Superposition von Basiszuständen:
   ci  i
mit
i
c
i
2
1
i
für zwei Basiszustände: „qubit“
● (max.)
verschränkter Zustand zweier Systeme:
 
1
2
(0 0 1 1)
bzw.
 
1
2
(0 1 1 0)
Dabei bei beliebiger gleichartiger Messung an beiden Systemen stets
perfekte Korrelation zwischen den Messergebnissen
(„spukhafte Fernwirkung“ Einsteins) !
Das Protokoll der Quantenteleportation
1993 von C.H.Bennett et al.
vorgeschlagen
Ziel: Sender Alice teleportiert
unbekanntes qubit 1 im Zustand

A
 a0 0  a1 1
1
2
3
an Empfänger Bob
Dabei:
● benutzen verschränkten Quantenpaares 2 und 3 bei Alice mit Zustand

●
●
23

1
2
(0 1 1 0)
A. macht sog. Bell-Zustandsmessung an Quant 1 und 2, wodurch
Quant 3, das über Quantenkanal an Bob geschickt, in eindeutigen
Zustand projeziert
Ergebnis dieser Messung wird über klass. Kanal (2-bit) an Bob
übermittelt, der mit dieser Kenntnis sein Quant in gewünschten
Zustand überführt
„no-cloning“-Theorem
Bei Bell-Zustandsmessung keine Kenntnis über einzelne Zustände;
 A wird zerstört.
Dies muss so sein wegen „no-cloning“-Theorem:
„Ein unbekannter Quantenzustand kann nicht perfekt
kopiert werden“
Beweis: ● Annahme: es gibt Quantenkopierer, also unitäre Zeitentwicklung
mit   h   
●
anwenden auf Basiszustände 0 und
1
:
0 h  0 0
1 h  1 1
●
damit ergibt sich für allg. Superpos.zustand
  0   1 :
( 0   1 ) h   0 0   1 1   
Widerspruch!!

Konkrete Rechnung zum Protokoll:
●
zu teleportierender Zustand 
Zustand 
23

1
2
A
 a0 0  a1 1 und verschränkter
( 0 1  1 0 ):
→Zustand aller drei Teilchen: 123  12 * A
●

a0

a1
2
2
(0
(1
A
A
0
0
2
2
13 0
131
A
A
1
1
2
2
0 3)
0 3)
darstellen in Basis der Bell-Zustände (entspricht Projektion von Quant 1 und
2 bei Bell-Zustandsmessung; dabei
12  12 ( 0 1 1 2  1 1 0 2 )
alle Ergebnisse gleich wahrschein
lich:
12
 12 ( 0 1 0 2  1 1 1 2 )
W  14
)
→
123  12 [ 12 (a0 0 3  a1 1 3 )  12 (a0 0 3  a1 1 3 )


 12
(a0 1 3  a1 0 3 )  12
(a0 1 3  a1 0 3 )]
123  12 [ 12 (a0 0 3  a1 1 3 )  12 (a0 0 3  a1 1 3 )


 12
(a0 1 3  a1 0 3 )  12
(a0 1 3  a1 0 3 )]
Interpretation
●
Superpos. von möglichen Gesamtzuständen von 1,2 und 3

Also: Bell-Zustandsmessung: Quant 1 u 2 in Zustand 12
Quant 3 in Zustand (a0 0  a1 1 )   A
usw.
→
●
bei 12 : Quant bei Bob bis auf Phasenfaktor (Minuszeichen) schon
in gewünschtem Zustand !(→Experiment)
sonst: entsprechende Operation anwenden:(entspricht Kombinationen
aus bit-flip 0  1 und
 { 2 ,  x ,  y ,  z }
phase-flip der relativen
Phase um  )
→  
3
A
Experimentelle Realisierung des Protokolls
1997 durchgeführt von
der Gruppe um A. Zeilinger
in Insbruck
●
benutzt werden Photonen und
deren Eigenschaft der Polarisation, also Basiszustände { H , V }
●
zur Erzeugung eines verschr.
Zustandes 23  12 ( H 2 V 3  V 2 H 3 )
und des Photons von Alice wird
Pumplaser auf nichtlinearen Kristall gestrahlt
●
Bell-Zustandsmessung durchStrahlteiler und Detektoren f1 und f2
●
mit polarisierendem Strahlteiler überprüft Bob, ob sei Photon im richtigen
Zustand ist
●
hier wird nur bei Bell-Messung von Zustand 23 Teleportation überprüft, d.h., nur in 1/4 der Fälle, in dem Photon 3 schon im richtigen
Zustand!
Quelle verschränkter Photonen
●
●
treten zu fester Frequenz auf Kegelmantel aus
An Überschneidungspunkten verschränkter Photonen im Zustand

●
Pumplaser (Pulsdauer:~ 200fs) auf
Bariumborat-Kristall (BBO)
→ durch spontane parametr.
Fluoreszens Typ II
zwei Photonen,
die stets orthogonal bzgl. Polarisation

1
2
(H V V H )
Nach durchtreten durch Kristall wird Pumpstrahl reflektiert und erzeugt zweites Photonenpaar
→ ein Photon ignoriert (bzw. zur Triggerung),
anderes trägt nach Projektion durch Polarisator
Zustand
 A  a0 H  a1 V
von Alice
Falschfarbenaufnahme
Bell-state-Messung
Photonen auf BS:
f1
Was passiert?
f2
Vier Möglichkeiten, die 4 Bellzuständen entsprechen:

12
Jedoch: Wird bei f1 und f2 gleichzeitig ein Photon detektiert, so wurden
beide reflektiert und sind also dannach in Zustand
12 
1
2
( H 1 V 2  V 1 H 2 ) (total antisymm.) !!
denn: - Situation 1 und 2 nicht möglich da Photonen nach Messung unterschiedliche Polarisationen haben müssen!
- Situation 3 und 4 als q.m. Superposition für Ergebnis „in jedem
Ausgang ein Photon“ mit destruktiver oder konstrukt. Interferenz
(wie bei Doppelspalt)

- Rechnung zeigt: Zustand 12 entspricht destruktiver Interferenz!
Dies ergibt sich auch durch die quantenmechanische Rechnung:
blablalbalbalbalbalbalblablablab
Experimentelle Durchführung
●
Zustand A und pol. BS bei Bob
so gewählt, das bei korrekter Teleportation d2 klickt
→ 3-fach-Koinzidenz (f1f2d1) als Nachweis korrekter T.,falls alle Photonen
korrekt erzeugt(!), denn:
T
beachte: „Falschevents“ werden
gezählt wenn statt Alice‘s Photon zweites verschränktes Paar (nach rechts)
erzeugt wird; dies geschieht mit gleicher Wahrscheinlichkeit
→ Ausschalten durch 4-fach-Koinzidenz (Tf1f2d1)
●
um Photonen vor BSM bzgl. Ankunftszeit ununterscheidbar zu machen
wird Bandbreitenfilter bei 788nm mit Breite 4nm benutzt
→Koinzidenzzeit von 520fs > Pulsdauer des Pumplasers
●
●
Durchfahren des T.bereiches durch Verschieben des Reflektionsspiegels
●
Messen für Grundzustände ( H  0, V  90 ) und Superpos. (±45°,..)
Ergebnisse
theoretisch erwartetes
Verhalten
Messwerte für ±45°-Polarisation:
bei 3-fach-Koinzidenz und Rausrechnen
der „Falschereignisse“ von (68±1)% durch
Messung bei blockiertem Photon 1
●
visibility des ‚dips‘ bei +45°-, -45°-,
0°-, 90°- und zirkular polarisierten Photonen von
((63, 64, 66, 61, 57) ± 2)% bei 3-fach-Koinzidenzmessung
●
bei 4-fach Koinzidenz (entspr. Projektion von
Photon 1 in Ein-Teilchen-Zustand!):
(70±3)%
für 45° und 90°
Donau-Experiment (Zeilinger et al. 2004)
Realisierung des experimentellen Aufbaus unter realistischen Bedingungen:
Erzeugung der Photonen wie
oben, aber:
●
Alice und Bob sind
600m voneinander entfernt
→Quantenkanal ist 800m
lange optische Faser unter
der Donau
●
Bell-Zustandsmessung unterscheidet zwei Zustände:
- klick bei 2 Detektoren des selben pol.BS

Zustand
12 
1
2
(H 1V
2
V
1
H 2)
- klick bei einem Horizontal- beim anderen Vertikal-Detektor

Zustand
12 
1
2
(H 1V
2
V
1
H 2)
●
Ergebnis der Messung wird über Funk an Bob gesandt,
bevor sein Photon ankommt (‚feed forward‘)!
Dies ist möglich durch verminderte Signalgeschw. in Faser (2/3xc) und
zusätzliche 200m Faser
→ Zeitvorsprung von 2 µs


● wird
23 übermittelt, muss relative Phase um

geändert werden durch
Anlegen von 3,7kV an elektro-optischen Modulator (EOM):
●
Ergebnis: - Effizienz von 50% (2 Bell-Zustände!)
- Teleportation von 45°-, linkszirkular und horizontal polar.
Photonen mit fidelity F von 0.84, 0.86 und 0.90 mit
F :  A Out A dA
●
technische Daten: - Pumplaser: 394nm
- Photonenpaar: 788nm
- Messdauer: 28h bei 0,04 erfolgreichen Teleport.
pro Sek.
- Polarisationsunsicherheit von 800m-Faser: ±10%
→ ideale fidelity von 0.97
Alternative Realisierung: time-bins
●
Energie-Zeit-verschränkte Photonen:
Basiszustände sind sog. time-bins
{ long , short }
durch unbalanciertes, zweiarmiges Interferometer realisiert
●
Gangunterschied (long-short) entspricht Zeitdifferenz
=1,5ns >> 150fs Pulsdauer

→ am Ausgang 2 definierte Pulse
●
Aufbau
Pulsstrahl (710nm) wird aufgeteilt:
- ein Teil in Interfer.(Phase  =0) →
  c0 long  c1ei short
und geht durch Lithiumtriborat-Kristall
→  
1
2
( short
C
short
i

e
long
B
verschr. Photonenpaar mit
C
long B )
 = 1,31µm (Charlie) und  = 1,55µm
(Bob)
- anderer Teil auch durch LBO und 1,31µm-Photon in Faser-Interfer. mit
einstellbarem (im Exp. 0, 50 und 100%) Faserkoppler und relat.Phase 
→ A  a0 long
●
i

a
e
short
1
1
1
BZM wie bei Phot. mit 4-fach-Koinzidenz
(Pumplaser,C1,C2,B), d.h., auch hier nur
Teleportation bei Ergebnis
23 ,
aber hier triggert C1 nur C2 und B, wenn
Zeitdiff. t zwischen klick bei C1 und C2
gleich
aus Interferr.!!

●
B mit A verbunden über 2km Faser
●
Analyse von Bob:
umgedrehtes Faser-Interferometer:
Überprüfen des teleport. Zustandes
mit gleichem Faserkoppler und Durchfahren von Phase 
(adaptiert für  =1,55µm)
●
Darstellung als Zustandsvektor auf PoincaréSphäre: Phase 
↔ Längengrad
Amplit. a0 , a1 ↔ Breitengrad
Pole: reine Basiszustände
a0  a1  1 2
Äquator: Superpos. mit
●
Ergebnisse:
-■: Messung der Konstanz des Aufbaus: (C1,B)
-○: Zustand
1
2
( long  short )
:
visibility: (70±5)%
→ fidelity: (85±2,5)%
- Basiszustände long
bzw.
short
:
fidelity: (77±3)% bzw. (88±3)%
 Fges = (81,2 ± 2,5)% > 66,7% ohne Verschr.
Weitere Alternativen
●
●
Teleportation kontinuierlicher Variablen, z.B. Amplitude
Lichtfeldern ( theoret.: Furusawa et al. 1998
exp.: Bowen et al. 2003 )
2
von
Teleportation von Zuständen(Spin!) von Ionen in Paulfallen:
Verschränkung,Bell-Messung etc. durch Laserpulse auf die Ionen und
el.mag. Wechselwirkung zwischen mehreren Ionen in einer Falle
→Teleportation nur über μm-Bereich zwischen benachbarten Fallen,
aber: Lebensdauern und Ionen mit ~100% detektierbar
Exp. Schließt das Detektionsschlupfloch in Argumentation
des lokalen Realismus
●
Teleportation von „Gequetschheit“: squeezed light beams
Lichtfeld in Fourierentwicklung (Superposition ∞ vieler Schwingungen ):
Rauschen (durch q.m.Unschärfe) in einer Mode kann zu(un)gunsten einer
anderen unterdrückt werde → „gequetschter Zustand“, der auch teleportiert
werden kann
Anwendung: genauere Messung physik. Größen (Gravitationswellen)
●
Teleportation von Makrozuständen der Ensemblen von Atomen:
- wie bei Photonen werden Zustände (Gesamtheit der Spins) von
Ensemblen erzeugt,verschränkt und teleportiert.
Dabei werden sie über Wechselwirkung eine äußeren Feldes mit
den Gesamtspins dem Ensemble aufgeprägt und
auch ausgelesen
Anwendungen
i) entanglement-swapping:
BZM
Y
X
A
B
- es wird Zustand X über verschränktes
Paar A und B auf B teleportiert, der selbst
verschränkt ist mit Y

Verschränkungen wechseln von
(A↔B) und (Y↔X) nach
(Y↔B) und (X↔A) !
D.h., dass 2 Photonen, die keinerlei gemeinsame Vergangenheit haben,
sich also nie „getroffen“ haben, miteinander verschränkt werden!!
(realisiert 1998 von Weinfurter et al. )
- Aneinanderreihung dieses Aufbaus mit BSM+Zustandsreinuger(repeater)
als unbegrenzt (durch Photonenverlust in Leitungen) lange Quantenleitung
für verschränkte Zustände
- interessant: Was passiert, wenn erst B und Y gemessen und dann BZM ?
2 bit
ii) dense-coding:
- Alice und Bob erhalten je ein
Photon eines verschränkten Paares
Alice
- nun kann Alice ihr Photon
manipulieren und an Bob schicken
Obwohl sie also nur ein Teilchen übermittelt, kann sie 2 bit an Information übermitteln:
2 bit
Bob
- durch die Manipulationen (Rotationen) an Alice‘s Photon werden beide
Photonen in einen von den 4 Bellzuständen projeziert, den Bob nach
Erhalten beider Photonen bestimmen kann
Diese Information entspricht 2 bit : 00,01,10,11
Ausblick
●
Verschränkung sehr vieler Zustände (Quanteninterferenzen!)
→ Teleportation komplexer Systeme: Moleküle,… ( Sinn?)
●
Weite Teleportation: Telep. zwischen Erde und Satellit durch die
Atmosphäre (ARTEMIS..)
●
Teleportation in Quantenkryptographie
→ abhörsichere Datenübertragung
●
entanglement swapping + Quantenspeicher
→ vernetzte Quantencomputer
●
Algorithmen auf verschränkte Ensembles
→ („one-way“-)Quantencomputer, die „schwere“ Probleme schnell lösen
Quellen
● „Teleporting an Unknown Quantum State via Dual Classical and
Einstein-Podolsky-Rosen Channels“, Charles H. Bennett et al.
Physikal Review Letters 70, No.13 (1993)
● „Experimental quantum teleportation“, A. Zeilinger et al.
Nature 390, 575 (1997)
● „Quantum teleportation across the Danube“, A.Zeilinger et al.
Nature 430, 849 (2004)
● „Long-distance teleportation of qubits at
telecommunication wavelengths“
I.Marcikic,H.deRiedmatten,W.Tittel,H.Zbinden,N.Gisin
Nature 421, 509 (2003)
● „Pulsed Energie-Time Entangled Twin-Photon Source
for Quantum Communication“; J. Brendel,N.Gisin,W.Tittel,H.Zbinden
Physikal Review Letters 82, No.12 (1999)
● Physik Journal, November 2005
● „Einsteins Spuk“, Anton Zeilinger; C.Bertelsmann Verlag 2005
● „Teleportation of atomic ensemble quantum states“; Dantan et al. Feb. 2006