Vortrag kurz

Quantenteleportation
Vortrag zum Seminar
„Moderne Experimente der Quantenoptik und Atomphysik“
von
Tobias M. Weber
Inhaltsübersicht
•
•
•
•
•
•
Einleitung
Theorie: Protokoll nach Bennett et al.
Experiment: Zeilinger et al.
Varianten der exp. Realisierung
Anwendungen
Ausblick
Was ist Quantenteleportation, was nicht?
● keine Realisierung der klass. Vorstellung
von Teleportation (science fiction), bei der
Masse (Person!) über große Strecken
ohne Verzögerung bewegt wird
● Übertragung des Zustandes eines
Quantensystems auf anderes mittels
klass.(z.B.Funk-) und eines Quantenkanals
(tragende Struktur also schon vor Ort)
Einhalten aller physikal. Gesetze, insbesondere Einsteins
Postulat der Lichtgeschwindigkeit als absolute Grenze bei
Signalübertragung
Wiederholung
● q.m.
Zustand als Superposition von Basiszuständen:
   ci  i
mit
i
c
i
2
1
i
für zwei Basiszustände: „qubit“
● (max.)
verschränkter Zustand zweier Systeme:
 
1
2
(0 0 1 1)
bzw.
 
1
2
(0 1 1 0)
→ bei beliebiger gleichartiger Messung an beiden Systemen
perfekte Korrelation zwischen den Messergebnissen
(„spukhafte Fernwirkung“ Einsteins) !
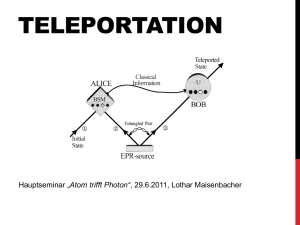
Das Protokoll der Quantenteleportation
1993 von C.H.Bennett et al.
vorgeschlagen
Ziel: Sender Alice teleportiert
unbekanntes qubit 1 im Zustand

A
 a0 0  a1 1
1
2
3
an Empfänger Bob
●
benutzen verschränkten Quantenpaares 2 und 3

●
23

1
2
(0 1 1 0)
Alice macht Bell-Zustandsmessung an Quant 1 und 2
→ Quant 3 bei Bob projeziert in eindeutigen Zustand
●
Ergebnis der Messung über klass. Kanal
→ Bob kann Photon 3 in gewünschten Zustand A bringen
„no-cloning“-Theorem
bei Bell-Zustandsmessung wird Zustand

A
zerstört
Dies muss so sein wegen „no-cloning“-Theorem:
„Ein unbekannter Quantenzustand kann nicht perfekt
kopiert werden“
Beweis: ● Annahme: es gibt Quantenkopierer, unitäre Zeitentwicklung
mit

 h   
●
anwenden auf Basiszustände 0 und
1
:
0 h  0 0
1 h  1 1
●
damit ergibt sich für allg. Superpos.zustand
  0   1 :
( 0   1 ) h   0 0   1 1   
Widerspruch!!
Konkrete Rechnung zum Protokoll:
●
zu teleportierender Zustand
Zustand

23

1
2
A
 a0 0  a1 1 und verschränkter
( 0 1  1 0 ):
→Zustand aller drei Teilchen:
●

123  12 * A

a0

a1
2
2
(0
(1
A
A
0
0
2
2
13 0
131
A
A
1
1
2
2
0 3)
0 3)
darstellen in vollständiger Basis der Bell-Zustände ( entspricht Messung an
Quant 1 und 2 )
  1 ( 0 1  1 0 )
12

12

2
1
2
1
2
1
2
( 0 1 0 2  1 1 1 2)
dabei: alle Ergebnisse gleich
wahrscheinlich:
W1
4

123  12 [ 12 (a0 0 3  a1 1 3 )  12 (a0 0 3  a1 1 3 )


 12
(a0 1 3  a1 0 3 )  12
(a0 1 3  a1 0 3 )]
123  12 [ 12 (a0 0 3  a1 1 3 )  12 (a0 0 3  a1 1 3 )


 12
(a0 1 3  a1 0 3 )  12
(a0 1 3  a1 0 3 )]
Interpretation
●
Superpos. von möglichen Gesamtzuständen von 1,2 und 3:

Bell-Zustandsmessung: Quant 1 u 2 in Zustand 12
→
Quant 3 in Zustand (a0 0  a1 1 )   A
usw.


12 : Quant bei Bob bis auf Phasenfaktor schon in gewünschtem
● bei
Zustand!
sonst: entsprechende Operation   { 2 ,  z ,  x ,  y } anwenden
(entspricht Kombinationen aus bit-flip 0
phase-flip der relativen Phase um
)

  3   A
1
und
Experimentelle Realisierung des Protokolls
1997 durchgeführt von
der Gruppe um A. Zeilinger
in Insbruck
●
●
Photonen und deren Polarisation
→ Basiszustände { H , V }
Erzeugung von verschr.
Zustand 23 
1
2
(H
2
V 3V
2
H 3)
mit Pumplaser auf nichtlinearen Kristall
●
●
Bell-Zustandsmessung durch Strahlteiler (Spiegel) und Detektoren f1 u f2

nur bei Bell-Messung von Zustand 23 Teleportation überprüft,
d.h., nur in 1/4 der Fälle, in denen Photon 3 schon im richtigen Zustand!
Quelle verschränkter Photonen
●
Pumplaser auf Bariumborat-Kristall :
spontane parametr. Fluoreszens
Typ II
→ zwei Photonen, die stets orthogonal
bzgl. Polarisation
●
treten zu fester Frequenz auf Kegelmantel aus;
an Überschneidungspunkten: verschränkte Photonen

●

1
2
(H V V H )
Erzeugen von zweitem Photonenpaar
→ ein Photon ignorieren (bzw. zur Triggerung),
anderes trägt nach Polarisator Zustand

A
 a0 H  a1 V
von Alice
Falschfarbenaufnahme
Bell-state-Messung
Photonen auf BS:
f1
Was passiert?
f2
Vier Möglichkeiten, die 4 Bellzuständen entsprechen:

12
Jedoch: f1 und f2 detektieren gleichzeitig ein Photon
→ beide im Zustand


12

1
2
( H 1 V 2  V 1 H 2)
!!
denn: - Situation 1 und 2 nicht detektierbar, da beide in einem Ausgang
- Situation 3 und 4 als q.m. Superposition für Ergebnis „in jedem
Ausgang ein Photon“ mit destruktiver oder konstrukt. Interferenz
- Rechnung zeigt: Zustand 12 entspricht
destruktiver Interferenz!
q.m. Rechnung
^
^
bH , bV
^
^
aH , aV
mit
^
^
^
^
d H , dV
c H , cV
 12 
1
2
bH 
1
2
(d H  ic H )

V
b 
1
2
(d  ic )
aH 
1
2
(cH  id H )
aV 
1
2
(cV  idV )

V

V
(bH aV 0  bV aH 0 )  ...






 12 (2ic H cV  2idV d H ) 0

1
2
(2d H cV  2cH dV ) 0
1
2
1
2
Experimentelle Durchführung
●
pol. BS bei Bob entsprechend A
so gewählt, dass bei korrekter Teleportation d2 klickt
→ 3-fach-Koinzidenz (f1f2d1) als Nachweis korrekter Teleportation
●
T
„Falschevents“ :
mit gleicher Wahrscheinlichkeit wie Photon 1
wird stattdessen zweites Photonenpaar (nach rechts) erzeugt!!
→ Ausschalten durch 4-fach-Koinzidenz (Tf1f2d1)
●
Durchfahren des T.bereiches durch Verschieben des Reflektionsspiegels
●
Messen für Grundzustände ( H  0, V  90 )
und Superpos. (±45°,..)
Ergebnisse
theoretisch erwartetes
Verhalten
●
3-fach-Koinzidenz und Rausrechnen
der „Falschereignisse“ von (68±1)%
visibility des ‚dips‘ bei +45°-, -45°-,
0°-, 90°- und zirkular polarisierten Photonen von
((63, 64, 66, 61, 57) ± 2)%
●
Messwerte für ±45°-Polarisation:
(bei 3-fach-Koinzidenzmessung)
bei 4-fach Koinzidenz (Projektion von 1 in Ein-Teilchen-Zustand!):
(70±3)%
für 45° und 90°
Donau-Experiment (Zeilinger et al. 2004)
Realisierung des experimentellen Aufbaus unter realistischen Bedingungen:
Erzeugung der Photonen wie
oben, aber:
●
Quantenkanal ist 800m
lange optische Faser unter
der Donau ( AB =600m)
●
Bell-Zustandsmessung:
zwei Zustände unterscheidbar:
12 
1
2
(H 1V
2
V
1
H 2)
1
H 2)
und
12 
1
2
(H 1V
2
V
durch 2 pol. Strahlteiler → 4
Detektoren
●
‚feed forward‘ des Messergebnisses
möglich durch verminderte Signalgeschw. in Faser (2/3xc) und
zusätzliche 200m Faser
→ Zeitvorsprung von 2 µs
●
●
23
gemessen: Anlegen von 3,7kV an elektro-optischen Modulator (EOM)
→ relat. Phase um
geändert

Ergebnis: - Effizienz von 50% (2 Bell-Zustände!)
- 45°-, linkszirkular und horizontal polar. Photonen mit
fidelity F von 0.84, 0.86 und 0.90
F :  A  Out A dA
●
technische Daten: - Pumplaser: 394nm
- Photonenpaar: 788nm
- Polarisationsunsicherheit von 800m-Faser: ±10%
→ ideale fidelity von 0.97
Alternative Realisierung: time-bins
●
Energie-Zeit-verschränkte Photonen:
Basiszustände sind time-bins
{ long , short }
durch unbalanciertes, zweiarmiges
Interferometer realisiert
→ Ausgang: Superpos.zustand
von kurzer und langer Flugzeit
(bzw. zweier zeitversetzter Pulse)
  c0 long  c1ei short
●
durch nichtlin. Kristall (LBO)
→ entsprechender verschränkter
Zustand
 
1
2
( short
C
short
i

e
long
B
C
long B )
Aufbau
Faser-Interfer. mit Faserkoppler und relat.Phase
→
i
●
A  a0 long 1  a1e short
●
1
4-fach-Koinzidenz (Pumplaser,C1,C2,B)
mit tC1C2   ,

also auch hier nur betrachten bei 12
●
Analyse von Bob:
umgedrehtes Faser-Interferometer
mit variabler Phase 

bei Alice
●
Ergebnisse:
-■: Messung der Konstanz des Aufbaus:
(C1,B)
-○: Zustand
1
2
( long  short )
:
visibility: (70±5)%
→ fidelity: (85±2,5)%
- Basiszustände long
bzw. short
fidelity: (77±3)% bzw. (88±3)%
 Fges = (81,2 ± 2,5)% > 66,7% : theoretisch maximal
erreichbar ohne Verschr.
:
Weitere Alternativen
●
Teleportation kontinuierlicher Variablen, z.B.
Lichtfeldern
Amplitude
2
von
( theoret.: Furusawa et al. 1998
exp.: Bowen et al. 2003 )
●
Teleportation von Zuständen(Spin!) von Ionen in Paulfallen:
z.B. Verschränkung durch Laserpulse und el.mag. Wechselwirkung
zwischen mehreren Ionen in einer Falle
→Teleportation nur über μm-Bereich aber Ionen mit ~100% detektierbar
Exp. schließt das Detektionsschlupfloch in Argumentation
des lokalen Realismus
(Barrett et al. oder Riebe et al. 2004; siehe Quellen)
●
Teleportation von „Gequetschheit“: squeezed light beams
Lichtfeld als Superposition ∞ vieler Schwingungen:
Rauschen in einer Mode zu(un)gunsten einer
anderen unterdrückt
→ „gequetschter Zustand“
kann auch zwischen 2 Lichtstrahlen teleportiert werden
Anwendung: genauere Messung physik. Größen (Gravitationswellen)
Anwendungen
i) entanglement-swapping:
- Was passiert, wenn verschränktes Photon
teleportiert ?
BZM
Y
X
A
B

Verschränkungen wechseln von
(A↔B) und (Y↔X)
nach (Y↔B) und (X↔A) :
2 Photonen ohne gemeinsame Vergangenheit miteinander verschränkt!
(realisiert 1998 von Weinfurter et al. )
- Aneinanderreihung dieses Aufbaus
→ unbegrenzt lange Quantenleitung für verschränkte Zustände
2 bit
ii) dense-coding:
- Alice und Bob erhalten je ein
Photon eines verschränkten Paares
Alice
- Alice kann Photon
manipulieren und an Bob schicken
2 bit
Bob
→ nur ein Teilchen, aber 2 bit an Information übermittelt:
- Manipulationen entspricht Projektion in einen der 4 Bellzuständen
→ 2 bit Information: 00,01,10,11
Ausblick
●
Teleportation komplexer Systeme: Moleküle,… (Quanteninterferenzen!)
●
Weite Teleportation: zwischen Erde und Satellit durch die
Atmosphäre (ARTEMIS..)
●
Teleportation in Quantenkryptographie
→ abhörsichere Datenübertragung
●
entanglement swapping + Quantenspeicher
→ vernetzte Quantencomputer
Quellen
● „Teleporting an Unknown Quantum State via Dual Classical and
Einstein-Podolsky-Rosen Channels“, Charles H. Bennett et al.
Physikal Review Letters 70, No.13 (1993)
● „Experimental quantum teleportation“, A. Zeilinger et al.
Nature 390, 575 (1997)
● „Quantum teleportation across the Danube“, A.Zeilinger et al.
Nature 430, 849 (2004)
● „Long-distance teleportation of qubits at
telecommunication wavelengths“
I.Marcikic,H.deRiedmatten,W.Tittel,H.Zbinden,N.Gisin
Nature 421, 509 (2003)
● „Pulsed Energie-Time Entangled Twin-Photon Source
for Quantum Communication“; J. Brendel,N.Gisin,W.Tittel,H.Zbinden
Physikal Review Letters 82, No.12 (1999)
● Physik Journal, November 2005
● „Einsteins Spuk“, Anton Zeilinger; C.Bertelsmann Verlag 2005
● „Teleportation of atomic ensemble quantum states“; Dantan et al. Feb. 2006