Quantenteleportation mit Photonen
Werbung

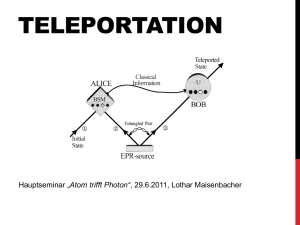
Quantenteleportation mit Photonen Peter Sprau Universität Würzburg 10.06.2009 Gliederung 1.) Theorie nach Bennett et Al. 2.) Experimentelles Teleportieren mit Photonen (Zeilinger et Al.) 3.) Realisierung von Gates über Teleportation (Gottesman and Chuang) 4.) Fazit 1. Theorie Grundidee Alice teilt Informationen von Zustand |F> in klassischen und nichtklassischen Teil auf Bob kann mit diesen Replik von |F> erstellen Dabei wird Alice Zustand zerstört => no-cloning – Theorem erfüllt klassische Informationsübertragung wird zwingend benötigt => kein Informationsübertrag mit Überlichtgeschwindigkeit Teleportation mit Spin - ½ Teilchen 1. Schritt ist die Präparation eines maximal verschränkten Zustandes zweier Teilchen 2 und 3, z.B. EPR-Singulett-Zustand (EPR = Einstein Podolsky Rosen): • Teilchen 2 wird nun an Alice übergeben und Teilchen 3 an Bob • Weiterhin besitz Alice Zustand |f1> von Teilchen 1, der übertragen werden soll: Mit: Teleportation mit Spin - ½ Teilchen Nächster Schritt ist die Verschränkung von Teilchen 1 mit 2 über eine vonNeumann- Messung in der Bell-Operator-Basis Diese besteht aus: Teleportation mit Spin - ½ Teilchen Vor dieser Messung befindet sich das gesamte System in einem reinen Produktzustand: Oder in Bell-Operator-Basis geschrieben als: Teleportation mit Spin - ½ Teilchen Durch die Projektionsmessung wird der Gesamtzustand auf einen der reinen Zustände reduziert: Wie man leicht sehen kann ist die Wahrscheinlichkeit für alle diese Zustände ¼ Dabei ist einer der ursprüngliche um eine Phase verschobene Zustand und die anderen drei sind jeweils noch rotiert worden Teleportation mit Spin - ½ Teilchen Alice besitzt nun einen der 4 BellZustände und Bob einen der reinen Zustände Nun muss Alice Bob nur noch auf klassische Art mitteilen, welchen Bellzustand sie gemessen hat Mit dieser Information kann Bob dann eine unitäre Transformation (Rotation) ausführen um den Anfangszustand zu erhalten |f1> wurde also bei Alice vernichtet und taucht als |f3> bei Bob auf => „Quantum State Teleportation“ Verallgemeinerung der Theorie 1.) Da die Teleportation eine lineare Operation ist, können statt reinen auch gemischte oder verschränkte Zustände teleportiert werden 2.) Funktioniert auch mit Systemen, die N>2 orthogonale Zustände besitzen: Statt einem EPR – Singulett würde ein komplett verschränkter Zustand aus den N orthogonalen Zustanden folgender Form benutzt werden: mit: Statt in der Bell-Operator-Basis könnte man eine Messung durchführen dessen Eigenzustände folgende Form hätten: Mit der entsprechenden unitären Transformation: 2. Experiment Experimenteller Aufbau Erzeugung der Photonen Ein UV-Puls mit einer Pulslänge von 200fs und einer Repetitionsrate von 76MHz wird auf einen nichtlinearen Kristall geschickt Über „Parametric Down Conversion“ (PDC) werden zwei verschränkte Photonen (2 und 3) mit einer Wellenlänge von 788nm erzeugt Der Puls wird an einem Spiegel reflektiert und tritt noch mal in den Kristall ein, Photonen 1 und 4 werden erzeugt Erzeugung der Photonen Die verschränkten Photonen die durch PDC erzeugt werden befinden sich im Singulettzustand Ihre Kohärenzzeit beträgt 520fs Messung in der Bell-OperatorBasis Um Photon 1 und 2 in einen Bellzustand zu projizieren, müssen sie ununterscheidbar gemacht werden => Superposition der Photonen an Strahlteiler Wenn nun an den Detektoren f1 und f2 gleichzeitig ein Signal beobachtet wird befinden sich die Photonen im Zustand |Y-12> Bestätigung der Teleportation Bob muss mit einem polarisierenden Strahlteiler und Detektoren dann nachweisen, dass er den selben Zustand für Photon 3 erhält, der vorher für Photon 1 existierte Durchführung des Experiments – „Beweisidee“ Fragestellung: Wie zeigt man, dass wirklich ein unbekannter Zustand teleportiert wurde? Idee: Zeige es zuerst für eine komplette Basis Hier +45°-, und -45°-linear polarisiert Vertikal und horizontal polarisiert wurde wegen der Vorzugsrichtung im Experiment nicht benutzt Zeige es anschließend für eine Superposition, was hier zirkular polarisiertem Licht entspricht Durchführung des Experiments für +45°-linear polarisiertes Photon Durchführung des Experiments für +45°-linear polarisiertes Photon Photonen werden erzeugt Photon 1 wird zu +45°-linear polarisiert Wenn Detektoren f1 und f2 Koinzidenz anzeigen folgt, dass Bellzustand vorliegt Bob misst mit polarisierendem Strahlteiler, +45° = Signal bei d2, -45° = Signal bei d1 D.h. Existenz von DreifachKoinzidenz d2f1f2 und Abwesenheit von DreifachKoinzidenz d1f1f2 bestätigt Teleportation Was bedeutet hier „delay“? Delay wird über Verschieben des Spiegels hinter Kristall erzeugt Dadurch wird die Ankunftszeit des Photons am Strahlteiler bei Alice verändert Ab einem gewissen Delaywert können Photonen zeitlich unterschieden werden => kein Bellzustand mehr Konsequenzen des „delay“ Photon 1 und 2 können jeweils zu 50% bei f1 oder f2 detektiert werden => Koinzidenz nun zu 50% statt 25% wie für Bellzustand Photon 3 ist nun jedoch ohne eindeutige Polarisation => kann zu 50% bei d1 oder d2 detektiert werden In Folge dessen erhält man für 25% +45° und für 25% -45° Messergebnisse Man sieht gute Übereinstimmung zwischen Theorie und Experiment Messergebnisse Hier wurde nur gemessen, wenn Photon 4 detektiert wurde, um Falsche Dreifach-Koinzidenz auszuschließen (bei sonstigen Messungen musste Untergrund Abgezogen werden) Messergebnisse Für verschiedene Polarisationen konnte Teleportation beobachtet werden 3. Gates mittels Teleportation Generelle Idee Benutze einen anderen verschränkten Eingangszustand U|Y> statt |Y>, wobei U eine nichttriviale Quantenoperation ist Für bestimmte Operatoren U kann gezeigt werden, dass exakt U|a> erhalten wird, wenn |a> der zu teleportierende Zustand ist Das Hadamard-Gate Statt dem verschränkten Zustand |Y> wird ein modifizierter Zustand benutzt Zitat aus [Got99] :“do nothing to the first qubit and apply H to the second qubit“ Teleportationsprotokoll als Skizze B = Bell state measurement X,Z = unitary transformations Das Ergebnis fürs Hadamard-Gate Man erhält dann zuerst HRxy|a>, wobei Rxy eine der unitären Transformationen ist, die bei der Projektionsmessung auf die Bellzustände auftreten Es gilt jedoch die Kommutatorrelation : HRxy=Rx‘y‘H D.h. durch Anwenden von R†x‘y‘ erhält man H|a> 4. Fazit Quantenteleportation bietet die Möglichkeit Informationen in einem „Quantencomputernetzwerk“ von einem Ort an einen anderen zu bringen, z.B. zur Weiterverabeitung Es wird weder Wissen über den zu teleportierenden Zustand benötigt noch über den Aufenthaltsort des Empfängers Aber es wird immer klassische Kommunikation benötigt Bietet die Möglichkeit Quantum – Computing auf der Basis von linear Optik zu realisieren 5. Quellenverzeichnis [BOU97] [KWI95] [Got99] [Ben93] Dik Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred Eibl, Harald Weinfurter & Anton Zeilinger Experimental quantum teleportation (Nature, 1997) Paul G. Kwiat, Klaus Mattle, Harald Weinfurtner, Anton Zeilinger, Alexander V. Sergienko and Yanhua Shih New High-Intensity Source of Polarization-Entangled Photon Pairs (PRL, 1995) Daniel Gottesman & Isaac L. Chuang Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations (Nature, 1999) Charles H. Bennett, Gilles Brassard, Claude Crepeau, Richard Jozsa, Asher Peres and William K. Wootters Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels (PRL, 1993)