Schätzung der Modellparameter

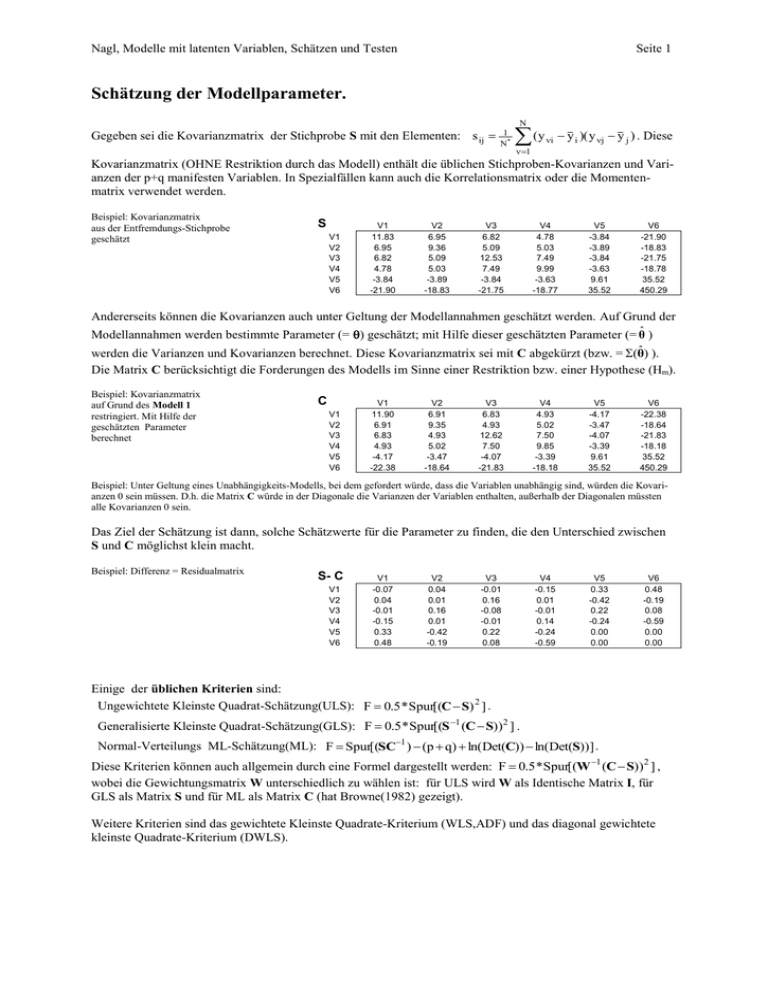
Nagl, Modelle mit latenten Variablen, Schätzen und Testen
Seite 1
Schätzung der Modellparameter.
N
Gegeben sei die Kovarianzmatrix der Stichprobe S mit den Elementen: s ij 
1
N*
 (y
i
 y i )( y j  y j ) . Diese
 1
Kovarianzmatrix (OHNE Restriktion durch das Modell) enthält die üblichen Stichproben-Kovarianzen und Varianzen der p+q manifesten Variablen. In Spezialfällen kann auch die Korrelationsmatrix oder die Momentenmatrix verwendet werden.
Beispiel: Kovarianzmatrix
aus der Entfremdungs-Stichprobe
geschätzt
S
V1
V2
V3
V4
V5
V6
V1
11.83
6.95
6.82
4.78
-3.84
-21.90
V2
6.95
9.36
5.09
5.03
-3.89
-18.83
V3
6.82
5.09
12.53
7.49
-3.84
-21.75
V4
4.78
5.03
7.49
9.99
-3.63
-18.77
V5
-3.84
-3.89
-3.84
-3.63
9.61
35.52
V6
-21.90
-18.83
-21.75
-18.78
35.52
450.29
Andererseits können die Kovarianzen auch unter Geltung der Modellannahmen geschätzt werden. Auf Grund der
Modellannahmen werden bestimmte Parameter (= ) geschätzt; mit Hilfe dieser geschätzten Parameter (= θ̂ )
werden die Varianzen und Kovarianzen berechnet. Diese Kovarianzmatrix sei mit C abgekürzt (bzw. = (θˆ ) ).
Die Matrix C berücksichtigt die Forderungen des Modells im Sinne einer Restriktion bzw. einer Hypothese (Hm).
Beispiel: Kovarianzmatrix
auf Grund des Modell 1
restringiert. Mit Hilfe der
geschätzten Parameter
berechnet
C
V1
V2
V3
V4
V5
V6
V1
11.90
6.91
6.83
4.93
-4.17
-22.38
V2
6.91
9.35
4.93
5.02
-3.47
-18.64
V3
6.83
4.93
12.62
7.50
-4.07
-21.83
V4
4.93
5.02
7.50
9.85
-3.39
-18.18
V5
-4.17
-3.47
-4.07
-3.39
9.61
35.52
V6
-22.38
-18.64
-21.83
-18.18
35.52
450.29
Beispiel: Unter Geltung eines Unabhängigkeits-Modells, bei dem gefordert würde, dass die Variablen unabhängig sind, würden die Kovarianzen 0 sein müssen. D.h. die Matrix C würde in der Diagonale die Varianzen der Variablen enthalten, außerhalb der Diagonalen müssten
alle Kovarianzen 0 sein.
Das Ziel der Schätzung ist dann, solche Schätzwerte für die Parameter zu finden, die den Unterschied zwischen
S und C möglichst klein macht.
Beispiel: Differenz = Residualmatrix
S- C
V1
V2
V3
V4
V5
V6
V1
-0.07
0.04
-0.01
-0.15
0.33
0.48
V2
0.04
0.01
0.16
0.01
-0.42
-0.19
V3
-0.01
0.16
-0.08
-0.01
0.22
0.08
V4
-0.15
0.01
-0.01
0.14
-0.24
-0.59
V5
0.33
-0.42
0.22
-0.24
0.00
0.00
V6
0.48
-0.19
0.08
-0.59
0.00
0.00
Einige der üblichen Kriterien sind:
Ungewichtete Kleinste Quadrat-Schätzung(ULS): F  0.5 * Spur[(C  S) 2 ] .
Generalisierte Kleinste Quadrat-Schätzung(GLS): F  0.5 * Spur[(S 1 (C  S)) 2 ] .
Normal-Verteilungs ML-Schätzung(ML): F  Spur[(SC1 )  (p  q)  ln(Det(C))  ln(Det(S))] .
Diese Kriterien können auch allgemein durch eine Formel dargestellt werden: F  0.5 * Spur[(W 1 (C  S)) 2 ] ,
wobei die Gewichtungsmatrix W unterschiedlich zu wählen ist: für ULS wird W als Identische Matrix I, für
GLS als Matrix S und für ML als Matrix C (hat Browne(1982) gezeigt).
Weitere Kriterien sind das gewichtete Kleinste Quadrate-Kriterium (WLS,ADF) und das diagonal gewichtete
kleinste Quadrate-Kriterium (DWLS).
Nagl, Modelle mit latenten Variablen, Schätzen und Testen
Seite 2
Bemerkungen zum ML-Kriterium für normalverteilte Daten:
Es wird unterstellt, dass die (p+q) Variablen in der Population normalverteilt sind. Im zentrierten Fall (alle Mity 
y 
1
telwerte gleich 0) gilt die Dichte: f (  ) 
exp(  12 (y  x  C 1  ) . Dabei ist C die Vari(
p

q
)
x
 
x
(2)
Det (C)
anz-Kovarianzmatrix ( der y- und x-Werte) in der Population, die auf Grund des Modells in einem gedachten
Generierungprozess entstanden ist.
Für eine Stichprobe der Größe N kann die Likelihood folgendermaßen dargestellt werden 1:
N


1


L
exp(  12 ( N Spur(S C 1 ) )) bzw.

(
p

q
)
 (2)
Det (C) 

ln(L)  0.5((p  q) N ln(2)  N ln(Det(C))  N Spur(SC1)) .
N
(( p  q) ln( 2)  ln( Det (C))  Spur(SC 1 )) . Diese Likelihood wird
2
maximiert durch die Variation der Parameterwerte, die dann ML-Schätzer heißen.
Nach Ausklammern von N: ln( L)  
Mit Hilfe dieser Likelihood wird ein Likelihood-Ratio-Test konstruiert, indem das Modell mit dem saturierten
Modell verglichen wird.
Das saturierte Modell hat exakt so viele Parameter wie die Elemente der Kovarianzmatrix. Ohne Restriktion ist
daher die restringierte Kovarianzmatrix C gleich S.
Das Maximum von Ln( Likelihood ) kann daher in diesem Fall folgendermaßen vereinfacht werden:
N
N
sup ln(L)   (( p  q) ln(2)  ln(Det (S))  Spur(SS 1 ))   (( p  q) ln( 2)  ln( Det (S))  (p  q))
2
2
saturiert
Der nat. Log. des Likelihood-Verhältnis ist:
sup (L)
ln()  ln( Modell Re str )  sup (ln( L))  sup (ln( L)) 
sup (L)
Modell Re str
Saturiert
Saturiert
 N
  N

  (( p  q) ln( 2)  ln( Det (C))  Spur(SC 1 ))    (( p  q) ln( 2)  ln( Det (S))  (p  q)) 
 2
  2

N
  (ln( Det (C))  ln( Det (S))  Spur(SC 1 )  (p  q)) .
2
Der negative verdoppelte natürliche Logarithmus des Likelihood-Verhältnisses ist unter Geltung der Hypothese (=Modellrestriktion) approximativ Chi**2 – verteilt:
 2 ln()  N(ln(Det(C))  ln(Det(S))  Spur(SC1 )  (p  q))  N FM ~ 2 (df ) .
Die Freiheitsgrade df werden i.a. folgendermaßen berechnet:
df = Anzahl der Parameter des saturierten Modells – Anzahl Parameter des restringierten Modells
Bemerkungen zum ‚Basis’-Modell bzw. Null-Modell.
Das ‚Unabhängigkeitsmodell wird oft auch als Basismodell bezeichnet (manchmal auch als Null-Modell). Die
ML-Schätzung des Unabhängigkeitsmodells sieht für die Kovarianzmatrix in der Diagonalen Varianzen, außerhalb der Diagonalen 0-en vor.
1
Hier wird momentan die Unterschiedlichkeit von N (wegen Erwartunbgstreue-Überlegungen vernachlässigt).
 N  1, falls Kovarianz bwz. Korrelatio n analyssiert wird
Sonst gelten folgende Ankürzungen: N *  
falls keine Mittelwert e geschätzt werden.
 N,
Nagl, Modelle mit latenten Variablen, Schätzen und Testen
Seite 3
Die so restringierte Matrix kann durch die Diagonalmatrix ML-geschätzt werden: C = Diag(S). Das ergibt für
das LR-Kriterium
 2 ln()  N(ln(Det(Diag(S)))  ln(Det(S))  Spur(SDiag(S) 1 )  (p  q)) = N( ln(s ii )  ln( Det (S)))

=: N*F0 =
mit:
 02 (df ).
df0 = (p+q) ((p+q)+1)/2 – (p+q) = (p+q)( (p+q+1)/2 – 1).
Einige Indizes zur Beurteilung der Anpassung (Fit).
GFI
1
Spur ( W 1 (S  C)) 2
1
Spur ( W (S))
AGFI
(p  q )( p  q  1)
1
(1  GFI )
2df
RMR
pq
2
( p  q )( p  q 1)
PGFI
Informationskriterien:
2
i
 (s
ij
 c ij ) 2
i 1 j1
df
GFI
df 0
AIC   2  2df
CAIC   2  (ln(N* )  1)df
LR-Test-Kriterium
RMSEA Index
Prob. of Close Fit
Z-Test (Wilson & Hilferty)
SBC   2  ln( N* )df
ECVI
 2 (df )
 a  max(
F
1

,0)
df N *
‚p-Wert’ für erweiterte H0
3 
df
2
Z
 (1  92df )
2
9df
Bentler-Bonett- Normed-Delta
F0  FM
F0
Goodness of Fit –Index (zwischen
0 und 1)
Adjustierter GFI
Wurzel aus dem Mittel der quadrierten Residuen
Parsimonious GFI (berücksichtigt
Abweichung vom Unabhängigkeitsmodell)
An Information Criterion
Consistent AIC
Schwarz-Bayes’sches C.
Expected Cross Validation Index
Anpassungs-Chi**2
Root-Mean-Square-Abweichung
(sollte in etwa ca. <= 0.05 sein)
H0: a0.05 (statt klassisch: a=0)
Approximation des –verteilten F
durch Normalverteilten z-Wert
Fehlerreduktion, Fehlermaß = F:
F0 Fehler bei Unabh.-Modell, FM =
Fehler bei vorliegendem Modell
df F0  FM
df 0
F0
Mit Abweichung vom Unabhängigkeitsmodell gewichtetes Delta
Bentler-Bonett- Non-Normed
F0 / df 0  FM / df
F0 / df 0  1 / N *
Fehlerreduktion, Fehlermaß = F
pro Freiheitsgrad
Normed Rho 1 (Bollen)
F0 / df 0  FM / df
F0 / df 0
Fehlerreduktion, Fehlermaß = F
pro Freiheitsgrad
Normed Delta 2 (Bollen)
F0  FM
F0  df / N *
Fehlerreduktion, Fehlermaß = F
Parsimonious Normed Fit (James,
Mulaik, Brett) Delta
Critical N Index
CN
‚Kritisches’ N: ab welchem N ist
das Ergebnis signifikant (auf 5%Niveau) wäre