1 Grundlagen

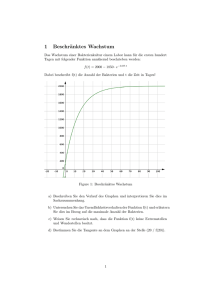
1
1.1
Grundlagen
Das Rechnen mit Zahlen
Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um:
N: natürliche Zahlen 1, 2, 3, 4, 5, . . .
Z: ganze Zahlen . . . , −3, −2, −1, 0, 1, 2, 3, . . .
Q: rationale Zahlen: das sind die Zahlen, die
man als Quotient pq zweier ganzer Zahlen
p und q schreiben kann.
Es gibt auch nicht rationale (irrationale) Zahlen, z.B.
√
2 oder π:
R: reelle Zahlen:
rationale und irrationale Zahlen.
Wenn wir uns auf die positiven (negativen) Zahlen beschränken wollen, setzen
wir ein hochgestelltes + (−) Zeichen hinter unser Symbol, also Z+, Q+ und R+
sowie Z−, Q− und R−. Beachte Z+ = N. Wenn wir in unsere Zahlbereiche auch
1
noch die 0 einschließen wollen, schreiben wir eine tiefergestellte 0 hinter unser
Symbol, also bezeichnet z.B. N0 die Zahlen 0, 1, 2, 3, . . .. Diese Menge bezeichnet
man auch als die Menge der nichtnegativen ganzen Zahlen!
Potenzen
Wir schreiben für das n-fache Produkt von a auch an:
a · a · a · · · a = an.
a Basis, n Exponent. Für das Rechnen mit Potenzen gelten Rechenregeln, die
wir aus der Schule als bekannt voraussetzen. Der Ausdruck 00 ist nicht definiert.
√
n
Die
Zahl b heißt die n-te Wurzel von b. Wir setzen hier b ≥ 0 voraus sowie
√
n
b ≥ 0. Die n-te Wurzel aus b ist diejenige nichtnegative Zahl x mit xn = b.
Wenn wir Ausdrücke der Form xy betrachten, dann können wir entweder x als
feste Größe und y als die Variable, oder umgekehrt x als Variable und y als
fest betrachten. Im ersten Fall sprechen wir von Exponentialfunktionen, im
zweiten Fall von Potenzfunktionen.
Exponentialfunktionen
2
Man macht sich das Verhalten der Exponentialfunktion am Besten an den zugehörigen Funktionsgraphen klar. Wir zeigen Ihnen hier einige Beispiele ax mit
a > 1 sowie 0 < a < 1. Beachten Sie den Unterschied: Ist a > 1, so ist die
Funktion wachsend, ist 0 < a < 1, so ist sie fallend. Es gilt stets a0 = 1,
d.h. die Funktionsgraphen von ax gehen stets durch den Punkt x = 0, y = 1,
unabhängig davon, wie a gewählt ist.
Einige Exponentialfunktionen a^x mit a>1
25
20
3^x
15
10
5
2^x
1.1^x
–3
–2
–1
0
1
2
x
3
3
Hier müssen wir etwas aufpassen. Der Graph der Funktion 1.1x sieht sehr flach
aus. Dem ist aber nicht so, wenn wir x groß wählen. Dann zeigt auch der Graph
von 1.1x exponentielles Wachstum:
1.1^x
100
80
60
40
20
–10
10
20
30
x
4
40
50
Einige Exponentialfunktionen a^x mit a<1
25
20
0.2^x
15
10
5
0.5^x
0.9^x
–2
–1.5
–1
–0.5
0
0.5
1
x
Potenzfunktionen
Wir kommen nun zu Potenzfunktionen. Wir beginnen mit einigen Beispielen xn
mit n ∈ N. Beachten Sie dabei bitte, dass die x-Achse (manchmal auch Abszisse
genannt) und die y-Achse (Ordinate) nicht denselben Maßstab haben!
5
Einige Potenzfunktionen x^n
x^4
15
10
5
x^2
–2
–1
0
1
2
x
x^1
–5
x^3
Wenn wir Potenzfunktionen xn betrachten mit n ∈ Z, n < 0, so sehen die
Funktionsgraphen etwas anders aus. Wir beschränken uns hierbei auf den Bereich
x > 0. Beachten Sie:
x−m =
1
xm ,
also z.B. x−2 = x12 . Wir erhalten den Graphen von x−2 aus dem von x2, indem
wir einfach die Kehrwerte der y-Werte (also der Ordinatenwerte) des Graphen
von x2 bilden:
6
Einige Potenzfunktionen x^n, n<0
120
x^(–4)
100
80
x^(–3)
60
40
x^(–2)
20
x^(–1)
0
0.2
0.4
0.6
0.8
1
x
7
1.2
1.4
1.6
1.8
2
Hier sind nun einige Funktionsgraphen von Potenzfunktionen mit rationalen Exponenten. Wir √
müssen uns auf den Fall x > 0 beschränken, weil z.B. Ausdrücke
1/2
wie (−1) = −1 gar nicht erklärt sind. Alle Graphen von Potenzfunktionen
xn gehen durch den Punkt x = 1 und y = 1, weil stets 1n = 1 gilt.
Beachten Sie:
√
p
x q = q xp .
Einige Potenzfunktionen x^n
4
3
x^2
2
x^(–1/2)
x^(–1/5)
1
x^(1/5)
x^(1/2)
0
0.2
0.4
0.6
0.8
1
x
Logarithmus
8
1.2
1.4
1.6
1.8
2