Folien 13.10.2014

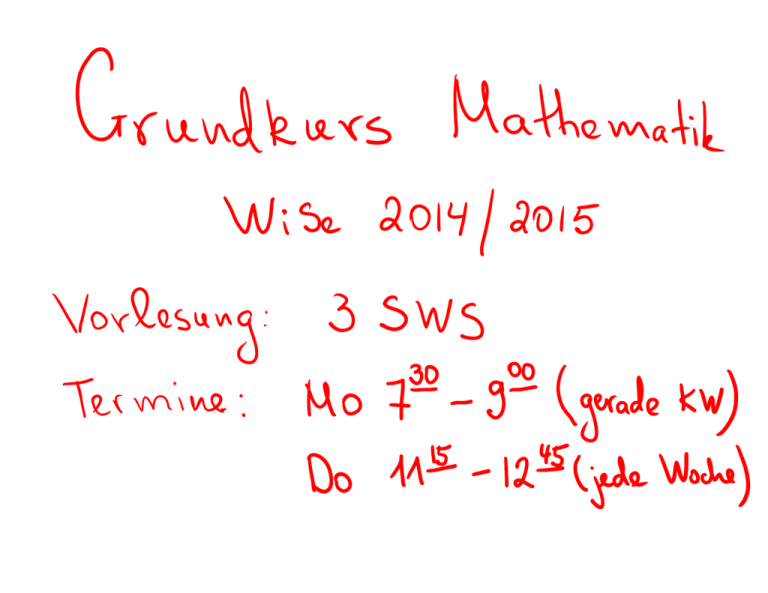
1
1.1
Grundlagen
Das Rechnen mit Zahlen
Wir gehen in dieser Vorlesung mit folgenden Zahlbereichen um:
N: natürliche Zahlen 1, 2, 3, 4, 5, . . .
Z: ganze Zahlen . . . , −3, −2, −1, 0, 1, 2, 3, . . .
Q: rationale Zahlen: das sind die Zahlen, die
man als Quotient pq zweier ganzer Zahlen
p und q schreiben kann.
Es gibt auch nicht rationale (irrationale) Zahlen, z.B.
√
2 oder π:
R: reelle Zahlen:
rationale und irrationale Zahlen.
1
Wenn wir uns auf die positiven (negativen) Zahlen beschränken wollen, setzen
wir ein hochgestelltes + (−) Zeichen hinter unser Symbol, also Z+, Q+ und R+
sowie Z−, Q− und R−. Beachte Z+ = N. Wenn wir in unsere Zahlbereiche auch
noch die 0 einschließen wollen, schreiben wir eine tiefergestellte 0 hinter unser
Symbol, also bezeichnet z.B. N0 die Zahlen 0, 1, 2, 3, . . .. Diese Menge bezeichnet
man auch als die Menge der nichtnegativen ganzen Zahlen!
2
Potenzen
Sei n eine natürliche Zahl. Wir schreiben für das n-fache Produkt von a auch an:
a · a · a · · · a = an .
a Basis, n Exponent. Für das Rechnen mit Potenzen gelten Rechenregeln, die
wir aus der Schule als bekannt voraussetzen.
Ist a 6= 0, wir definieren a0 = 1. Der Ausdruck 00 ist nicht definiert.
3
Wir definieren Potenzen auch mit negativen Exponenten:
a−n =
1
, für a 6= 0.
an
1/n
√
n
Es gibt auch Potenzen mit gebrochenen Exponenten. Die Zahl√b = b heißt
die n-te Wurzel von b. Wir setzen hier b ≥ 0 voraus sowie n b ≥ 0. Die n-te
Wurzel aus b ist diejenige nichtnegative Zahl x mit xn = b.
4
Wenn wir Ausdrücke der Form xy betrachten, dann können wir entweder x als
feste Größe und y als die Variable, oder umgekehrt x als Variable und y als
fest betrachten. Im ersten Fall sprechen wir von Exponentialfunktionen, im
zweiten Fall von Potenzfunktionen.
Exponentialfunktionen
Man macht sich das Verhalten der Exponentialfunktion am Besten an den zugehörigen Funktionsgraphen klar. Wir zeigen Ihnen hier einige Beispiele ax mit
a > 1 sowie 0 < a < 1.
Beachten Sie den Unterschied: Ist a > 1, so ist die Funktion wachsend, ist
0 < a < 1, so ist sie fallend.
Es gilt stets a0 = 1, d.h. die Funktionsgraphen von ax gehen stets durch den
Punkt x = 0, y = 1, unabhängig davon, wie a gewählt ist.
5
Einige Exponentialfunktionen a^x mit a>1
25
20
3^x
15
10
5
2^x
1.1^x
–3
–2
–1
0
1
2
3
x
Hier müssen wir etwas aufpassen. Der Graph der Funktion 1.1x sieht sehr flach
aus. Dem ist aber nicht so, wenn wir x groß wählen. Dann zeigt auch der Graph
von 1.1x exponentielles Wachstum:
6
1.1^x
100
80
60
40
20
–10
10
20
30
x
7
40
50
Einige Exponentialfunktionen a^x mit a<1
25
20
0.2^x
15
10
5
0.5^x
0.9^x
–2
–1.5
–1
–0.5
x
8
0
0.5
1
Potenzfunktionen
Wir kommen nun zu Potenzfunktionen. Wir beginnen mit einigen Beispielen xn
mit n ∈ N. Beachten Sie dabei bitte, dass die x-Achse (manchmal auch Abszisse
genannt) und die y-Achse (Ordinate) nicht denselben Maßstab haben!
Einige Potenzfunktionen x^n
x^4
15
10
5
x^2
–2
–1
0
1
x
x^1
–5
x^3
9
2
Wenn wir Potenzfunktionen xn betrachten mit n ∈ Z, n < 0, so sehen die
Funktionsgraphen etwas anders aus. Wir beschränken uns hierbei auf den Bereich
x > 0. Weil x−2 = x12 , erhalten wir den Graphen von x−2 aus dem von x2, indem
wir einfach die Kehrwerte der y-Werte (also der Ordinatenwerte) des Graphen
von x2 bilden:
10
Alle Graphen von Potenzfunktionen xn gehen durch den Punkt x = 1 und y = 1,
weil stets 1n = 1 gilt.
Einige Potenzfunktionen x^n, n<0
120
x^(–4)
100
80
x^(–3)
60
40
x^(–2)
20
x^(–1)
0
0.2
0.4
0.6
0.8
1
x
11
1.2
1.4
1.6
1.8
2
Hier sind nun einige Funktionsgraphen von Potenzfunktionen mit rationalen Exponenten. Wir √
müssen uns auf den Fall x > 0 beschränken, weil z.B. Ausdrücke
1/2
wie (−1) = −1 gar nicht erklärt sind. Beachten Sie:
p
xq =
√
q
xp .
Einige Potenzfunktionen x^n
4
3
x^2
2
x^(–1/2)
x^(–1/5)
1
x^(1/5)
x^(1/2)
0
0.2
0.4
0.6
0.8
1
x
12
1.2
1.4
1.6
1.8
2
Logarithmus
Die Umkehrung des Potenzierens ist das Logarithmieren.
Gilt ax = b, a, b > 0, a 6= 1, so heißt
x der Logarithmus von b zur Basis a.
Bezeichnung: x = loga(b).
Manchmal lassen wir die Angabe der Basis auch weg. Ist die Basis 10, sprechen
wir vom dekadischen Logarithmus. Ist a die Eulersche Zahl e ≈ 2, 7182 . . .,
heißt der Logarithmus natürlich. Der natürliche Logarithmus wird meistens mit
ln bezeichnet, der dekadische Logarithmus mit lg.
Wir halten noch einmal explizit fest:
aloga(b) = b
Für das Logarithmieren gelten Rechenregeln, die wir aus der Schule als bekannt
voraussetzen. Für die konkrete Berechnung von Logarithmen benötigt man eigentlich nur die Kenntnis der Logarithmen zu einer bestimmten Basis:
loga(b) =
13
logc(b)
.
logc(a)
Ähnlich wie im Fall von Exponential- und Potenzfunktionen zeigen wir Ihnen hier
die Funktionsgraphen einiger Logarithmusfunktionen. Man beachte, dass loga(x)
nur für a, x > 0 sowie a 6= 1 definiert sind. Es fällt auf: loga(1) = 0.
Einige Logarithmusfunktionen
2
log_0.5(x)
log_1.5(x)
1
log_3(x)
log_0.2(x)
0
0.2
0.4
0.6
0.8
1
x
–1
–2
14
1.2
1.4
1.6
1.8
2
1.2
Gleichungen und Ungleichungen
Ein zentrales Thema der Algebra ist das Lösen von Gleichungen. Ganz einfach
ist dies für sogenannte lineare Gleichungen
a·x=b
Wenn hier a 6= 0 ist, können wir beide Seiten der Gleichung durch a dividieren
und erhalten als Lösung x = ab .
Die positive Lösung einer Potenzgleichung der Form
xa = b, b > 0
√
√
1
a
a
ist x = b = b . Beachte: Der Ausdruck a b ist vereinbarungsgemäß immer positiv.
Man beachte den Unterschied zur Exponentialgleichung
ax = b, a, b > 0,
a 6= 1
Die Lösung der Exponentialgleichung ist x = loga(b).
15
Die Lösungen von quadratischen Gleichungen der Form
ax2 + bx + c = 0,
a 6= 0
sollten aus der Schule bekannt sein. Die Lösungen für a 6= 0 sind
√
−b ± b2 − 4ac
x± =
.
2a
Machen wir uns noch einmal klar, wie man auf diese Lösung kommt. Wir setzen
a 6= 0 voraus:
ax2 + bx + c = 0
b
c
x2 + x = −
a a2
2
b
b
b
c
x2 + x +
=− +
a
2a
a
2a
2
b
c
b2
x+
=− + 2
2a
a 4a
√
b
b2 − 4ac
x+
=±
,
2a
2a
16
und damit
√
b2 − 4ac
x± =
.
2a
Eine quadratische Gleichung hat keine oder nur eine oder zwei Lösungen:
−b ±
• Ist b2 − 4ac > 0, so gibt es zwei Lösungen.
• Ist b2 − 4ac = 0, so gibt es eine Lösung.
• Ist b2 − 4ac < 0, so gibt es keine Lösungen (weil es keine Wurzeln aus
negativen Zahlen gibt!).
Beachten Sie, dass sich die Lösungsformel vereinfacht, wenn a = 1 ist. Wir erhalten dann als Lösung der Gleichung
x2 + px + q = 0
die sogenannte p-q-Formel:
x± =
−p ±
p
2
17
p2 − 4q
Beispiel 1.1 Finde alle x mit
x+2=
√
4 − x.
(1.1)
Wir quadrieren beide Seiten und erhalten so
(x + 2)2 = 4 − x.
Also, weil (x + 2)2 = x2 + 4x + 4,
x2 + 4x + 4 = 4 − x
oder
x2 + 5x = 0
x(5 + x) = 0.
Das geht nur für x = 0 oder x = −5. Wir müssen jetzt aber aufpassen! Durch
das Quadrieren der Gleichung haben wir vielleicht unerwünschte neue Lösungen
erhalten. (Beispiel: x = −3, Quadrieren liefert x2 = 9, als Lösungen also x = ±3,
aber x = 3 war keine Lösung der ursprünglichen Gleichung!) Wir müssen also,
wenn wir beim Lösen von Gleichungen quadrieren, mit den erhaltenen Lösungen
immer eine Probe machen, d.h. in die ursprüngliche Gleichung einsetzen.
18
Wir machen
√ also die Probe: Setzen wir 0 in die Gleichung (1.1)
√ ein, so erhalten
wir 2 = 4, richtig. Beim Einsetzen von −5 ergibt sich −3 = 9, was falsch ist,
da die Wurzel stets positiv ist!
19