Verlaufsplanung

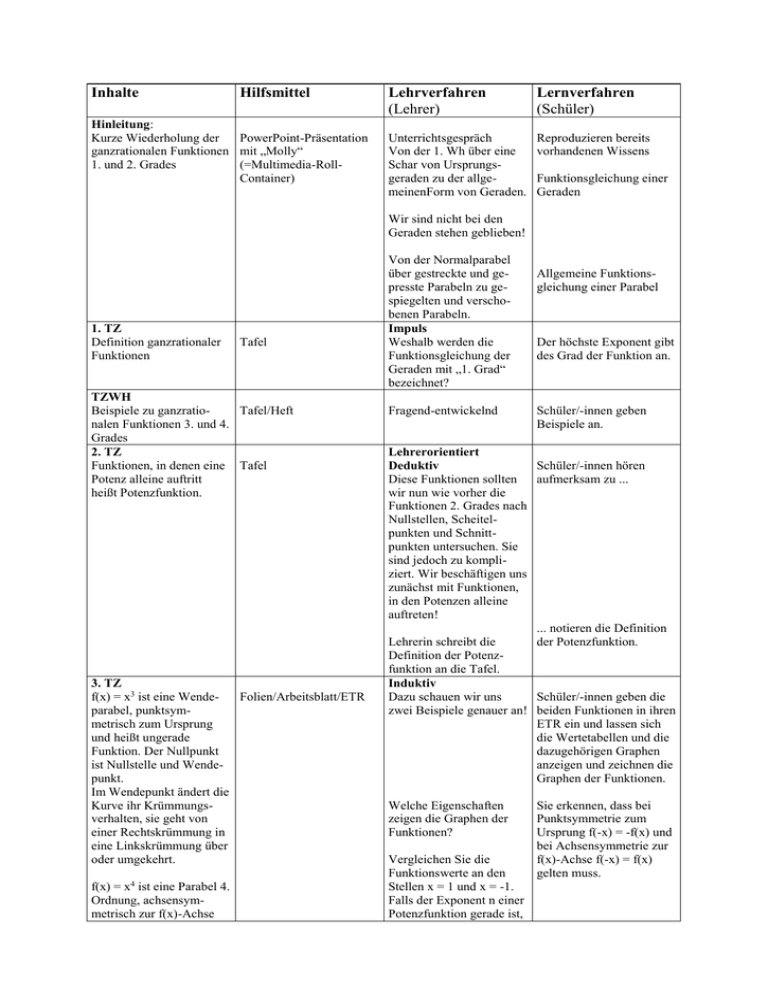
Inhalte
Hilfsmittel
Hinleitung:
Kurze Wiederholung der
PowerPoint-Präsentation
ganzrationalen Funktionen mit „Molly“
1. und 2. Grades
(=Multimedia-RollContainer)
Lehrverfahren
(Lehrer)
Lernverfahren
(Schüler)
Unterrichtsgespräch
Von der 1. Wh über eine
Schar von Ursprungsgeraden zu der allgemeinenForm von Geraden.
Reproduzieren bereits
vorhandenen Wissens
Funktionsgleichung einer
Geraden
Wir sind nicht bei den
Geraden stehen geblieben!
1. TZ
Definition ganzrationaler
Funktionen
Tafel
TZWH
Beispiele zu ganzratioTafel/Heft
nalen Funktionen 3. und 4.
Grades
2. TZ
Funktionen, in denen eine Tafel
Potenz alleine auftritt
heißt Potenzfunktion.
3. TZ
f(x) = x3 ist eine WendeFolien/Arbeitsblatt/ETR
parabel, punktsymmetrisch zum Ursprung
und heißt ungerade
Funktion. Der Nullpunkt
ist Nullstelle und Wendepunkt.
Im Wendepunkt ändert die
Kurve ihr Krümmungsverhalten, sie geht von
einer Rechtskrümmung in
eine Linkskrümmung über
oder umgekehrt.
f(x) = x4 ist eine Parabel 4.
Ordnung, achsensymmetrisch zur f(x)-Achse
Von der Normalparabel
über gestreckte und gepresste Parabeln zu gespiegelten und verschobenen Parabeln.
Impuls
Weshalb werden die
Funktionsgleichung der
Geraden mit „1. Grad“
bezeichnet?
Fragend-entwickelnd
Allgemeine Funktionsgleichung einer Parabel
Der höchste Exponent gibt
des Grad der Funktion an.
Schüler/-innen geben
Beispiele an.
Lehrerorientiert
Schüler/-innen hören
Deduktiv
Diese Funktionen sollten
aufmerksam zu ...
wir nun wie vorher die
Funktionen 2. Grades nach
Nullstellen, Scheitelpunkten und Schnittpunkten untersuchen. Sie
sind jedoch zu kompliziert. Wir beschäftigen uns
zunächst mit Funktionen,
in den Potenzen alleine
auftreten!
... notieren die Definition
Lehrerin schreibt die
der Potenzfunktion.
Definition der Potenzfunktion an die Tafel.
Induktiv
Dazu schauen wir uns
Schüler/-innen geben die
zwei Beispiele genauer an! beiden Funktionen in ihren
ETR ein und lassen sich
die Wertetabellen und die
dazugehörigen Graphen
anzeigen und zeichnen die
Graphen der Funktionen.
Welche Eigenschaften
zeigen die Graphen der
Funktionen?
Vergleichen Sie die
Funktionswerte an den
Stellen x = 1 und x = -1.
Falls der Exponent n einer
Potenzfunktion gerade ist,
Sie erkennen, dass bei
Punktsymmetrie zum
Ursprung f(-x) = -f(x) und
bei Achsensymmetrie zur
f(x)-Achse f(-x) = f(x)
gelten muss.
und heißt gerade Funktion.
Der Nullpunkt ist eine
Nullstelle, Tiefpunkt
(Minimum) und Scheitelpunkt.
TZWH
Weitere Beispiele zu
Potenzfunktionen höheren
Grades bestätigen das
Gelernte.
spricht man von geraden
Funktionen (AS), ist er
ungerade, so spricht man
von ungeraden Funktionen
(PS).
ETR/Folie/Arbeitsblatt
4. TZ
Schüler/-innen gewinnen
Molly
einen Überblick über die
verschiedenen ganzrationalen Funktionen
höheren Grades, begreifen
Zusammenhänge zwischen
Funktionsgleichungen und
Graphen. Sie lernen den
Einsatz dieser Funktionen
in der Betriebswirtschaftslehre kennen.
5. TZ
Durch Pressung, Dehnung, Arbeitsblätter mit LaufVerschiebung und
zettel und Lösungen.
Spiegelung ändern sich die
Potenzfunktionen.
Kommen in der
Funktionsgleichung nur
gerade Exponenten vor, so
ist der Graph achsensymmetrisch zur y-Achse,
treten nur ungerade Exponenten auf, so ist der
Graph punktsymmetrisch
zum Ursprung.
An einem Beispiel erkennen die Schüler/-innen,
dass eine ganzrationale
Funktion 3. Grades 3
Nullstellen, 2 Extrempunkte und 1 Wendepunkt
hat. Dementsprechend
In welchen Quadranten
verlaufen jeweils die
Kurven?
Die Parabeln gerader
Ordnung verlaufen vom II.
in den I. Quadranten, die
Parabeln ungerader
Ordnung vom III. in den I.
Quadranten.
Geben Sie in Ihren ETR
noch weitere Potenzfunktionen höheren
Grades ein und vergleichen Sie die Graphen!
Schüler/-innen erkennen,
dass Potenzfunktionen mit
geraden Exponenten eine
Achsensymmetrie aufweisen, also gerade
Funktionen sind. Potenzfunktionen mit ungeraden
Exponenten weisen eine
Punktsymmetrie auf und
sind somit ungerade
Funktionen.
Lehrerpräsentation
Stationenlernen mit der
Möglichkeit der Einzel-,
Partner- oder Gruppenarbeit.
Schülerorientiert
Stationenlernen mit der
Möglichkeit der Einzel-,
Partner- oder Gruppenarbeit.
Schüler/-innen verfolgen
die Präsentation.
In Einzel-, Partner- oder
Gruppenarbeit lösen die
Schüler/-innen die ihnen
auf den Arbeitsblättern
gestellten Aufgaben und
vergleichen die Ergebnisse
mit den Lösungen.
verhält sich eine ganzrationale Funktion 4.
Grades mit 4 Nullstellen, 3
Extrempunkten und 2
Wendepunkten.
Beim praktischen Beispiel
aus der Wirtschaft lernen
die Schüler/-innen die
Bedeutung der Nullstelle
an einer Gewinnfunktion
kennen.
Lernzielkontrolle:
Präsentation der ErgebFolien/Arbeitsblätter
nisse durch Schüler/innen.
Schülerorientiert
Zusammenführen der
Lerngruppen durch die
Präsentation der Ergebnisse.
Schwierige Passagen
werden besprochen und
Unklarheiten beseitigt.