Biologie 12 S.49 (Das HARDY-WEINBERG

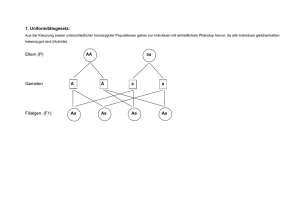
Das HARDY-WEINBERG-Gesetz



Wurde 1908 aufgestellt
Voraussetzungen für die Gültigkeit dieses Gesetzes:
- Ausgangspunkt ist eine Idealpopulation mit folgenden Bedingungen:
- Keine Mutationen
- Keine Selektion
- Unendlich große Population ohne Beeinflussung durch die Umwelt
- Vollständige Panmixie (jedes geschlechtsreife Individuum kann sich mit jedem anderen paaren)
- Kein Gendrift bzw. Genfluss
- Generationen überlappen nicht
HARDY-WEINBERG-Gleichgewicht: Die Allelhäufigkeiten in Populationen stehen in einem stabilen
Gleichgewicht zueinander
Gen A ist dominant, Gen B ist rezessiv
P (F1):
Aa
Gameten:
A
Aa
a
A
a
F2:
A
AA
p2
AA
q.p
A
a
A
Aa
p.q
aa
q2
Genotypisches Verhältnis: 1 : 2 : 1
Phänotypisches Verhältnis: 3 : 1
Gleichung:
p2 + 2pq + q2
(p + q) 2
p+q
=1
=1
=1
√
(gilt für die Ausgangspopulation)
p=1-q
q=1-p
Bsp.:
Die Häufigkeit der autosomal-rezessiven Erbkrankheit Mucoviscidose beträgt 1 : 2000. Zu berechnen
ist die Anzahl der heterozygoten Anlageträger.
P-Generation:
F1-Generation:
p+q =1
p2 + 2pq + q2 = 1
ges.:
geg.:
2pq (da heterozygot, siehe Vererbungsquadrat)
q2 = 1/2000
Lös.:
q = √ 1/2000 ≈ 0,0224
2 pq
= 2 (1 - q) ∙ q
 denn
= 2 (1 - √ 1/2000) ∙ √ 1/2000
Aa
≈ 0,044
≈ 4,44 %
 ∙ 100
- 49 -
p=1-q