Grundpraktikum

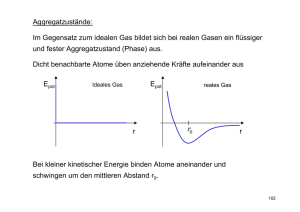
Versuchsprotokoll
Versuch 2:
Dampfdruckkurve
Gruppe 43: Annika Kroning, Alexandra Erdt, Jakob Machon
1 – fach Bachelor
Kolloquium: 23.06.06
Versuchstag: 29.06.06
1
1. Theoretische Grundlagen
1.1 Dampfdruck
Evakuiert man einen Behälter und füllt dann eine Flüssigkeit ein, so entsteht ein dynamisches
Gleichgewicht zwischen der flüssigen und der gasförmigen Phase. Der Dampfdruck stellt
diejenige Kraft dar, die die Teilchen der gasförmigen Phase auf die Innenfläche des Behälters
ausüben. Druck ist definiert als Kraft pro Fläche, demnach ist der Dampfdruck die Kraft der
Teilchen, die auf die Innenwände ausgeübt wird dividiert durch die Oberfläche des Behälters.
Der Dampfdruck ist temperaturabhängig: Bei einer bestimmten Temperatur weist er immer
denselben Wert auf. Bei einer Volumenänderung stellt sich das Gleichgewicht neu ein: Bei
Verkleinerung des Volumens gehen mehr Teilchen in die flüssige Phase über, bei Vergrößerung
des Volumens gehen mehr in die Dampfphase über.
Verbindungen oder Stoffe mit einem hohen Dampfdruck verdampfen schneller als solche mit
einem niedrigeren Dampfdruck, also ist der Dampfdruck ein Maß für die Flüchitgkeit eines
Stoffes.
Am Siedepunkt ist der Dampfdruck gleich dem Atmosphärendruck.
1.2 Phasenübergänge
Abb. 1: Phasendiagramm eines reinen Stoffes
Ein Phasendiagramm eines Stoffes ist eine graphische Darstellung der Druck – und
Temperaturbereiche, bei denen die einzelnen Phasen thermodynamisch stabil sind. Die drei
Kurven stellen jeweils die Grenzen zwischen den Phasen dar. An diesen Grenzen stehen die
beiden Phasen im Gleichgewicht. Ist der Umgebungsdruck gleich dem Dampfdruck, siedet eine
Flüssigkeit (Siedepunkt).
Es gibt zwei besondere Punkte im Phasendiagramm:
2
Tripelpunkt: An diesem Punkt treffen sich die drei Kurven. Hier liegen alle drei Phasen im
Gleichgewicht vor. Er ist für jeden Stoff spezifisch festgelegt. Es ist der niedrigste Punkt, an
dem der Stoff in der flüssigen Phase vorliegen kann.
Kritischer Punkt: Es ist das höchste Temperatur/Druck – Paar, an dem eine Flüssigkeit
existieren kann. Bei höherem Druck bzw. höherer Temperatur können Flüssigkeit und Gas nicht
mehr unterschieden werden.
1.3 Gibb`sche Phasenregel
Mit Hilfe der Gibb`schen Phasenregel lässt sich berechnen, wieviele Zustandsvariablen im
System verändert werden können, ohne dass sich die Phasen ändern:
F=K–P+2
F: Freiheiten (Anzahl der veränderbaren Zustandsvariablen)
K: Anzahl der Komponenten
P: Anzahl der Phasen
Am Tripelpunkt ist F = 1 – 3 + 2 = 0 (invariant), da keine der Zustandsvariablen (T, p) geändert
werden kann ohne eine Änderung des Phasengleichgewichts hervorzurufen. Auf den Kurven des
Phasendiagramms ist F = 1 – 2 + 2 = 1 (univariant), demnach kann eine der Variablen (T, p)
geändert werden. Die andere gleicht sich dann so der Änderung an, dass die Phasen wieder ins
Gleichgewicht kommen. Liegt nur eine Phase vor, so ist F = 1 – 1 + 2 = 2 (divariant), es können
also beide Variablen in gewissem Maße beliebig verändert werden, ohne dass sich die Phase
ändert.
1.4 Beschreibung der Verdampfungsenthalpie über die Gleichung von Clausius-Clapeyron
und Anwendung des Kirchhoff’schen Satzes
Am Phasenübergang sind die chemischen Potentiale der beiden Phasen gleich, es gilt
μgas=μflüssig
und
dμgas=dμflüssig
Außerdem gilt für d  S m dt  Vm dp . Ersetzt man die dμ durch die totalen Differentiale und
fasst zusammen, ergibt sich die Beziehung
dp S m

dT Vm
(1)
Da die beiden Phasen im Gleichgewicht stehen und somit der Vorgang reversibel ist, kann
man die Entropie durch die dabei umgesetzte Wärmemenge (die bei isobaren Prozessen gleich
der Änderung der molaren Enthalpie ist) und die zugehörige Temperatur ersetzen:
v S 
also gilt
dp  v H

dT T vV
v H
T
(Clausius – Clapeyron`sche Gleichung)
(2)
3
Mit ΔvV gleich der Differenz der Molvolumina (V(g) – V(l)).
Die Clausius – Clapeyron`sche Gleichung beschreibt die Steigungen der im Phasendiagramm
dargestellten Kurven, in diesem Fall die der Siedekurve.
Betrachtet man jetzt Moleküle von Gasen, stellt man fest, dass diese sich frei im Raum
bewegen können. Sie nehmen also den für sie frei zur Verfügung stehenden Raum komplett
ein. In Flüssigkeiten spielen jedoch intermolekulare Kräfte eine Rolle, von den die Moleküle
zusammengehalten werden.
Wenn der Temperatur – Druck – Bereich weit unterhalb der kritischen Temperatur und dem
kritischen Druck liegt, so ist VFlüss viel kleiner als VDampf und kann somit vernachlässigt
werden.
Die Clausius – Clapeyron`sche Gleichung kann zu folgender Gleichung vereinfacht werden:
H v
dp

dT T  VDampf
Für niedrige Dampfdrücke gilt für die Gasphase annähernd das ideale Gasgesetz.
Setzt man V 
RT
aus der Zustandsgleichung idealer Gase für VDampf ein, so ergibt sich:
p
H v
H v
H v  p
dp



RT
dT T  VDampf
R T 2
T
p
durch Umformen kommt man auf
H v
dp
dp

mit
 d ln p . Die Gleichung lautet dann:
2
pdT RT
p
d ln p H v

dT
RT 2
Durch Trennung der Integrationsvariablen p und T ergibt sich:
d ln p 
H v
 dT
RT 2
Handelt es sich um einen kleinen Temperaturbereich, so ändert sich H v kaum und kann
daher als konstant angesehen werden.
Unter Berücksichtigung dieser Bedingung integriert man nun die oben aufgeführte Gleichung
und zieht die Konstanten H v und R vor das Integral. Es ergibt sich somit:
ln
Da ln

p2 H v  H v


 ln p1 
p1
R  R  T1

p2
 ln p2  ln p1 kommt man durch erneutes Umformen der obigen Gleichung
p1
auf die Geradengleichung:
4
ln p2  

H v  H v
 
 ln p1 
R  T2  R  T1

Die Steigung dieser Gleichung lautet: m  
Wenn ln p gegen
H v
R  T2
1
aufgetragen wird, kann man H v aus der Steigung berechnen.
T
Um die ermittelten Daten mit den Literaturwerten vergleichen zu können, müssen die
Werte auf 25°C umgerechnet werden. Dazu muss der Kirchhoff’sche Satz angewendet
werden.
Kirchhoff’scher Satz:
T2
H v ,T2  H v ,T1   C p dT
T2
Für die Verdampfung ergibt sich dann:
T2
H vT2  H vT1   c p ( Dampf )  c p ( Flüssigkeit ) dT
T1
Innerhalb einer Phase verändert dich c p nur wenig. Somit kann man auch hier sagen,
dass c p konstant ist. Dieses gilt, wenn sich die Temperatur nicht stark verändert.
Letztendlich gilt also:
H v ,T2  H v ,T1  c p (T2  T1 )
1.5 Temperaturabhängigkeit der Verdampfungsenthalpie
Die Verdampfungsenthalpie ist temperaturabhängig. Sie nimmt mit steigender Temperatur zu,
bis der kritische Punkt erreicht ist. An diesem Punkt kann der Stoff nicht mehr flüssig
vorliegen, somit kann auch nichts verdampfen.
1.6 Troutonsche Regel
Die Verdampfungsentropie, die aus der Verdampfungsenthalpie der jeweiligen Flüssigkeit am
Siedepnkt bestimmt wird, ist im Mittel gleich groß. Sie streut um den Durchschnittswert
 verd S 
 verd H
= 88JK-1mol-1
TS
Bei Stoffen, die Wasserstoffbrückenbindungen ausbilden, liegt die Verdampfungsentropie
über 88J/Kmol. Der Grund dafür ist ihre geringe Entropie in der flüssigen Phase, da die
Moleküle durch die Wasserstoffbrücken geordneter vorliegen als bei Stoffen ohne
Brückenbindungen. In der Gasphase tre- ten die Wasserstoffbrücken nicht mehr auf, die
5
Entropieerhöhung ist also größer. Verbindungen mit Werten unter 88 J/Kmol bilden sowohl in
der flüssigen als auch in der Dampfphase intermolekulare Bindungen aus, sodass diese in
beiden Phasen geordneter vorliegen.
Für Stoffe, die dem Troutonschen Regelfall in etwa entsprechen, gelten folgende
experimentelle Tatsachen:

Schwingungsspektren von flüssiger und gasförmiger Phase unterscheiden sich kaum

Gleiches gilt für die Rotationen
→ Moleküle schwingen und rotieren in diesen beiden Phasen sehr ähnlich, somit müssen
wesentliche Änderungen der Energie und Entropie die Translation betreffen.
Man geht jetzt also davon aus, dass den Flüssigkeitsmolekülen Raum für Bewegungen
(insbesondere Translation) zur Verfügung steht. Demnach behandelt man eine Flüssigkeit wie
ein Gas und die Verdampfung wie die Expansion eines Gases. Dieser Raum wird freies
Volumen genannt und ist wesentlich kleiner als das Volumen der Gasbehälter.
Wird also das Gasmodell auf Flüssigkeiten angewandt, so steht NA Flüssigkeitsmolekülen ein
Raum von ca. 1cm3 für die Translation zur Verfügung.
1.7 Druckmessgeräte
Manometer: Das Manometer wird zur Messung von Gasdrücken in geschlossenen Systemen
verwendet. Es besteht aus einem am oberen Ende geschlossenen Glasrohr, welches mit Gas
gefüllt ist und in einem mit Quecksilber gefüllten Behälter steht. Durch das Eigengewicht des
Quecksilbers sinkt die Hg – Säule soweit, bis der von ihr ausgeübte Druck gleich dem Druck
entspricht, der auf den Quecksilberbehälter ausgeübt wird. Die Skalierung ist im Allgemeinen
so gewählt, dass die Hg – Säule an einem duchschnittlichen Tag auf Meereshöhe 760mm =
1Torr = 1atm hoch ist.
Barometer: Das Barometer hat eine ähnliche Funktionsweise wie das Manometer. Es wird
meist im Zusammenhang mit meteorologischen Messungen gebraucht. Dort hängt der
Luftdruck neben der Höhe auch von der Wetterlage ab.
2. Versuch
3.1 Versuchsaufbau:
6
Abbildung 1 Dampfdruckmessapparaturi
3.2 Versuchsbeschreibung
Mit der oben dargestellten Apparatur lassen sich statistische Dampfdruckmessungen
durchführen.
Die Temperatur lässt sich mit Hilfe eines Eisbades, das immer weiter erwärmt wird,
einstellen und der zugehörige Druck wird am Druckmessgerät abgelesen.
Die Pumpe ist in diesem Fall eine Drehschiebervakuumpumpe.
Damit eine Verunreinigung Pumpe verhindert wird, wird zwischen die Pumpe und den
Messkolben eine Kühlfalle geschlossen. Die Kühlfalle besteht aus einem Abscheidegefäß,
das in flüssigen Stickstoff taucht, welcher sich in einem DEWAR- Gefäß befindet.
Nun wird Hahn A geschlossen und die Vakuumpumpe auf Betriebtemperatur gebracht.
Bevor die Kühlfalle aufgebaut werden kann, müssen alle Schliffe mit Aceton gereinigt
und anschließend gefettet werden.
Dann wird der Rückflusskühler mit dem 100-ml Zweihalskolben „blindgeflanscht“.
Nun wird Hahn C geschlossen und Hahn B geöffnet und Hahn A wird so eingestellt, dass
die Apparatur bis ca. 1,0 mbar evakuiert werden kann.
Wenn Hahn B wieder geschlossen wird, darf sich das Vakuum nur geringfügig ändern.
Ändert es sich doch erheblich, müssen die Schliffe erneut überprüft werden.
Wenn alles dicht ist, wird Hahn C geöffnet und die Messung kann beginnen.
7
In den 2-Halkolben wird jetzt so viel Ethanol gefüllt, bis das Thermometer ca. 1 cm in die
Flüssigkeit taucht. Die Flüssigkeit wird mit einem Rührer gerührt, damit sich die Kälte
besser verteilen kann.
Hahn C kann nun wieder geschlossen werden.
In der Kunststoffschale kann nun Kältebad aus Eis und Wasser hergestellt werden. Der 2Halskolben wird nun bis zum Halsansatz in das Kältebad getaucht. Auch das Kältebad soll
gerührt werden.
Wenn eine konstante Temperatur erreicht ist, wird der Hahn B geöffnet und die
Messapparatur wird bis zum Sieden Evakuiert. Hahn B muss nun schnell wieder
geschlossen werden. Der nun entstehende Druck ist zu notieren.
Für die nächsten Messungen wird die Temperatur im Kältebad durch Entnahme von Eis
erhöht.
Die Apparatur soll zwischendurch nicht erneut evakuiert werden.
Messergebnisse:
Messung 1:
Temperatur
[K]
1/T
273
275
277
279
281
283
285
287
289
291
293
Druck
[mbar]
0,003663
0,00363636
0,00361011
0,00358423
0,00355872
0,00353357
0,00350877
0,00348432
0,00346021
0,00343643
0,00341297
ln(p)
19,9
23,1
26
28,7
32,3
34,9
38,8
44,5
47,8
50,6
53,3
2,99071973
3,13983262
3,25809654
3,35689712
3,47506723
3,55248683
3,65842025
3,79548919
3,86702564
3,92395158
3,97593633
Druck 1
[kPa]Druck
1,99
2,31
2,6
2,87
3,23
3,49
3,88
4,45
4,78
5,06
5,33
ln(p1)
0,68813464
0,83724752
0,95551145
1,05431203
1,17248214
1,24990174
1,35583515
1,4929041
1,56444055
1,62136648
1,67335124
Messung 2:
Temperatur
[K]
1/T
273
0,003663
275 0,00363636
277 0,00361011
Druck
[mbar]
ln(p)
17,1 2,83907846
20,3 3,01062089
23 3,13549422
Druck 2
[kPa ]
ln(p2)
1,71 0,53649337
2,03 0,70803579
2,3 0,83290912
8
279
281
283
285
287
289
291
293
0,00358423
0,00355872
0,00353357
0,00350877
0,00348432
0,00346021
0,00343643
0,00341297
26,1
29,6
33,1
37,8
42,5
45,7
49,2
52
3,26193531
3,38777436
3,49953328
3,6323091
3,74950408
3,8220983
3,89589362
3,95124372
2,61
2,96
3,31
3,78
4,25
4,57
4,92
5,2
0,95935022
1,08518927
1,19694819
1,32972401
1,44691898
1,5195132
1,59330853
1,64865863
Graphische Auswertung:
y(M1) = -3988,5x + 15,343
5
y(M2) = -4511,6x + 17,119
4,5
4
y(DDB1) = -5158,4x + 19,358
3,5
y(DDB2) = -4998,4x + 18,861
3
2,5
2
1,5
1
0,5
0
0,0029
0,00315
0,0034
0,00365
Messung 1
Messung 2
DDB1
DDB2
Linear (DDB2)
Linear (DDB1)
Linear (Messung 1)
0,0039 Linear (Messung 2)
HV
 HV  m  R . Somit
R
folgt hier für die von uns bestimmten Werte und die Vergleichswerte aus der Dortmunder
Datenbank:
J
kJ
H V  (3988,5K )  8,314
 33,16
mol  K
mol
J
kJ
H V  (4511,5K )  8,314
 37,51
mol  K
mol
J
kJ
H V  (5158,4 K )  8,314
 42,89
mol  K
mol
J
kJ
H V  (4998,4 K )  8,314
 41,56
mol  K
mol
Für die Verdampfungsenthalpie von Ethanol gilt: m  
i
Prof. Dr. K. Al-Shamery, Physikalische Chemie: Versuchsskript SS 06
9