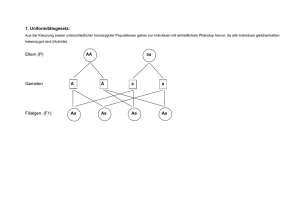
Was ist eine multiple Korrelation

Statistik II
Was ist eine multiple
Korrelation?
Beispiele für multiple
Korrelation
Karin Pilz







befasst sich mit dem Zusammenhang mehrerer Variablen untereinander
Voraussetzung für multiple Regression
Nullkorrelation (kein geeigneter Prädiktor, keine inkrementelle Validität
1 Prädiktor korreliert
inkrementelle Validität
keine inkrementelle Validität
Suppressor Effekt (Prädiktor korreliert nicht mit Kriterium aber mit anderem
VENN-DIAGRAMM lesen
Prädiktor
eine
Korrelation von 2 Variablen wird meist durch eine 3. Variable beeinflusst
Partialkorrelation rx1y.x2
durch Konstanthalten/Eliminieren der Drittvariablen wird diese aus beiden
Fragestellung
anderen herauspartialisiert

wie hoch ist der Gewichtsverlust Y vom Training X1 ab, wenn alle gleich
viel Kalorien X2 zu sich genommen hätten?
Korrelation der Variablen x1 und y nachdem x2 nur aus y herauspartialisiert
Semipartialkorrelation
wurde
rx1(y.x2)

Wie viel Varianz des Gewichtsverlustes y erklärt das Training x1
Fragestellung
zusätzlich zur Kalorienaufnahme x2?
Wie viel Varianz der abhängigen Variable (Kriterium) können durch die
Multiple Korrelation R y.x1x2
beiden UVs (Prädiktoren) gemeinsam aufgeklärt werden?

der multiple Korrelationskoeffizient erfasst den Zusammenhang zwischen
mehreren Prädiktorvariablen und einem Kriterium
Multiple Regression

Frage nach der Vorhersage einer aV durch mehrere uV
R

R: vereinigter Zusammenhang aller Prädiktoren mit dem Kriterium
R2

R2 : Anteil der durch alle Prädiktoren aufgeklärten Varianz (Maß für die
Güte der Vorhersage bei der multiplen Regression)

R2y.x1x2 = r2yx1 + r2y(x1.x2)

Bestimmung über Kriterium der kleinsten Quadrate

(yi-y^i)2 = e2i
inkrementelle Validität
eine Variable besitzt inkrementelle Validität, wenn ihre Aufnahme als Prädiktor
(zusätzlich) den Anteil an Varianz (R 2) am Kriterium erhöht
R2y.x1x2 > r2yx1
Kriterium der kleinsten
Bei der Bestimmung der Vorhersagegerade wird das Kriterium der
Quadrate
kleinsten Quadrate angewandt, weil man die Summe der quadrierten
Vorhersagefehler minimieren will. Der Vorhersagefehler ist dabei die mittlere
quadrierte Abweichung der tatsächlichen y-Werte vom vohergesagten yWert
y^i = b1xi1 + b2xi2 + b3xi3+....+bkxik + ai (y = bx + a)
Strukturgleichung
yi = b1xi1 + b2xi2 + b3xi3+....+bkxik + ai + ei(y = bx + a)
Regressionskoeffizienten (b) 
b-Gewichte der Prädiktorvariablen sind das relative Gewicht einer
Prädiktorvariablen in der Vorhersage

Regressionsgewichte werden mit t-test auf Signifikanz geprüft
Regressionskonstante (a)

kann man errechnen durch Umstellen der Strukturgleichung

wird auch mit t-test auf Signifikanz geprüft
standardisierte

zyi = 1zi1 + 2zi2....+ k zik
Regressionsgewichte Beta

Vorteil: -Gewichte können wie Korrelationskoeffizienten interpretiert
werden, können nur Werte zwischen –1 und +1 annehmen, Konstante a
entfällt, weil MW z^y = 0
Signifikanztest bei multiple

durch F-Test über Zerlegung der Varianz des Kriteriums in erklärbare und
Regression und Korrelation
nicht erklärbare Varianz

SS total = SS reg + SS res

SStotal = (yi-yquer)2

SSreg =  (y^i - yquer)2 MSreg = SSreg / K (Anzahl der Prädiktoren)

SSres = (yi-y^)2 MSres = SSres / N-K-1 (N = Anzahl der Probanden)

F-Test = MSreg / MSres bzw F = R2/dfZähler / (1-R2)/dfNenner ;

R2 = SSreg / SStotal durch Umformen: SSreg = R2 / 1-R2 x SSres
2
korrigiertes R
R überschätzt Populationszusammenhang (Stichprobe zu Stichprobe oder
Population)

je kleiner Stichprobe und je größer die Anzahl der Prädiktoren, desto
größer die Überschätzung von R2

Empfehlung von N/K mind. 20

Korrekturformel anwenden (Schrumpfungskorrektur)
Seite 1 von 11
Statistik II
Capitalization of Chance
Wie kann man die b-Gewichte
prüfen?
Strategien der multiplen
Regression
Karin Pilz


einzelnen Korrelationen nicht fehlerfrei
bei Berechnung werden Prädiktoren, die zu hoher Korrelation führen,
bevorzugt, dadurch auch Erhöhung derFehler

Folge: systematische Überschätzung von R2
durch Kreuzvalidierung überprüfen der externen Validität

a priori Auswahl: theorie- und evidenzgeleitet werden inhaltlich
bedeutsame Prädiktoren aufgenommen ---- Einschlussverfahren
Vorteil: keine Capitalization of chance
Nachteil: F-Wert mindernd, weil evtl. zu viel Prädiktoren Folge: Power nimmt
ab

a posteriori: Prädiktorauswahl erfolgt über mehrere Regressionsanalysen
mit versch. Prädiktorsätzen:
Selektionsstrategien: Schrittweise Regression: Vorwärts Selektion,
Rückwärts Eliminieren (hierbei wird schrittweise nach jeder Aufnahme eines
Prädiktors über forward und backward untersucht, ob auf einen Prädiktor
verzichtet werden kann. Vorgang abwechselnd. Dadurch können Prädiktoren,
die ursprünglich viel Varianz aufgeklärt haben, jedoch durch Hinzunahme
SPSS-Ausgabe
weiterer überflüssig geworden sind, wieder herausgenommen werden
Interpretation
Nachteil: Capitiization of Chance, überprüfen durch Kreuzvalidierung
(Grundannahmen ALM

Der beobachtete Wert einer Vp in der aV setzt sich zusammen aus:
Strukturgleichung der ALM,
Gesamtmittelwert, Summe von gewichteten Weten der uV und einem
Matrixcodierung)
individuellen Fehler

Frage nach Unterschieden zwischen mehreren Gruppen

nach der ALM kann der Wert der aV für VPi in der Bedingung j geschätzt
werden als: yij = a0 + aj(gruppenspez. Effekt) + eij (Fehler)
Nicht wichtig (es gibt 2

a0 = yquer; aj = yiquer – yquer Effekt: Abweichung vom Gr.MW zum
unterschiedliche
GesamtMW, durch die Größe des Effekts, wie stark sich Teilgr. vom
Herangehensweisen:
Gesamtgr. unterscheiden

Strukturgleichung

daraus folgt: yij = yquer + (yiquer – yquer) + eij; Y = Xa +e

Quadratsummenzerlegun
a: Effekte
x: Indikatorvariable / Faktor
g

yi = a0xi0 + a1xi1 + a2xi2 + ....ap xip + ei (y=aV; p:Anzahl der uVn; xij:
werte von Person i auf der uVj)

Matritzenschreibweise: Y = X*a + e
(Randbedingungen der

Bedingung der kleinsten Quadrate, d.h. eine möglichst gute Schätzung der
Strukturgleichung)
Gruppenwerte durch Effekte:  e2i = minimal

Mittelwert der Fehler (eij) ist 0 (equerij = 0)
Nicht wichtig

Mittelwert der Effekte (aj) ist 0: aj = 0
(Dummy- und Effektcodierung) 
Dummycodierung: Effekt für letzte Gruppe kann nicht mehr angegeben
werden (nur verwenden, bei letzter Gruppe: KG) : yij = a0 + eij

Effektcodierung: alle Effekte spielen mit hinein: y13 = a0 + a3 + e13 (a1
Nicht wichtig
+ a2 +a3 = 0) yij = a0 + aj+ eij (Placebo)
Voraussetzungen der

mind. Intervallskalenniveau und Normalverteilung in der Stichprobe bei
Varianzanalyse
der aV

mind. 20 Elemente pro Gruppe / Zelle

ähnlich stark besetzte Gruppen / Zellen: nmax / nmin < 1,5

Varianzhomogenität der aV zwischen den einzelnen Stichproben
Vorgehen/Ablauf wichtig
(Levene, Bartlett, Hartley)
einfaktorielle Varianzanalyse bei Vergleich von Mittelwerten (2 Gruppen) entspricht Anova dem T-Test: F = t2
bei mehr Vergleichen entsteht alpha-Fehler Kummulierung oder Inflation
alpha-Fehler Inflation
bei mehr als 2 Vergleichen besteht die Gefahr fälschlicherweise einen
signifikanten Effekt (alpha=0,05) zu finden:
bei 3 Vergleichen:
die Wahrscheinlichkeit keinen Fehler zu machen: p(kein Fehler)= 1-alpha =
0,953 = 0,86
die Wahrscheinlichkeit mind. 1 Fehler zu machen: p(Fehler)= 1-p(kein Fehler)
= 1-(1-alpha)3 = 0,14
Bonferroni Korrektur

alpha-Niveau für jeden einzelnen Test herabsetzen

Nachteil: sehr niedriges alpha-Niveau, dadurch hohes beta und niedrige
Teststärke
Seite 2 von 11
Statistik II
Hypothesen der
Varianzanalyse
Karin Pilz
Ho:

alle Mittelwerte sind gleich: i =
j für alle i, j entspricht: σ2(µ) = 0

alle Effekte sind 0: i = 0 für alle
i

(Erwartungswerte)
Nicht wichtig
Erklärt, was hinter F-Test
steckt (Herleitung)
Für Durchführung der Anova
irrelevant

2
ist 0: Varianz von Effekt = 0
H1:

i ungleich j für mind. 1 Paar

mind. 1 Effekt ungleich 0: alphai
ungleich 0 für mind. ein i


2 > 0
ungerichtete Alternativhypothese,
sonst über Kontraste richten

Erwartungswerte schätzen, welche Werte unter der Bedingung Ho zu
erwarten sind

Vorgang: wenn man immer wieder würfelt und sich die Zahlen notiert, dann
kann man daraus einen Erwartungswert berechnen (Mittelwert)

bei Ho gilt: Mittelwerte gleich, Effektvarianz gleich 0
1.bei 2 Populationsverteilungen 1 = 2 = 7,5; identi. Fehlervarianzen: 21 = 2
2 = 2.25
2.aus jeder Pop wird eine Stichprobe N = 5 gezogen und die Varianz zwischen
Bed. gerechnet
3.Vorgang wird sehr oft wiederholt und Mittelwert (Erwartungswert) der beiden
Varianzen berechnet:
Varianz innerhalb: E(2^ innerhalb)=
2 innerhalb = 2 Fehler = 2,25
Varianz zwischen: E(2^ zwischen)= n2Effekt + 2 Fehler = 2,25, weil unter Ho ist
Effektvarianz = 0

unter Ho schätzt die Stichprobenvarianz innerhalb der Gr. die
Fehlervarianz in der Population

die Stichprobenvarianz zwischen den Gr. schätzt ebenfalls die
Fehlervarianz in der Population (weil Effektvarianz = 0)
bei H1 gilt: Mittelwerte ungleich, Effektvarianz > 0


2 Pop.verteilungen: 1=5; 2=10; Varianzen sind gleich = 2,25
nach mehrmaliger Ziehung wurde der Mittelwert (Erwartungswert) berechnet

E(2^ zwischen)= n2Effekt + 2 Fehler



= 2Effekt = (i- )2 / p-1= (5-7,5)2 + (10-7,5)2 / 1 = 12,5 dann oben
einsetzen = 64,75
unter H1 schätzt die Stichprobenvarianz innerhalb die Fehlervarianz in
der Pop
Stichprobenvarianz zwischen schätzt die Summe aus Effekt- und
Fehlervarianz in Pop

2zwischen/2innerhalb schätzt n2Effekt+ 2Fehler / 2 Fehler
wenn 1 herauskommt, gibt es keinen Effekt, also Ho (F=1)
wenn > 1, gibt es einen Effekt (F>1) Femp > Fkrit dann signifikanter Effekt
Fkrit abhängig von dfZähler und dfNenner
Levene Test


1.
2.
Interpretation der H1 in
Varianzanalyse bei mehr als
2 Gruppen
1.
2.



ist eine Varianzanalyse über die Abweichung der individuellen
Messwerte vom Gruppenmittelwert: dij = Iyij-yquerjI
Ho: dquer1 = dquer2=....dquerj
Berechnen in neuer Tabelle, F-Test: MSbetween / MS within
wird Levene-Test signifikant p<0,05, dann Annahme der
Varianzhomogenität verletzt
hier ist nicht klar, wo der Unterschied liegt
Lösung: Vergleich der einzelnen Mittelwerte:
a priori: Kontraste
post hoc: Tukey (sign. bei d> HSD), Scheffé
(t-test)
Seite 3 von 11
Statistik II
Karin Pilz
Vor- und Nachteile Kontraste
/ post-hoc Tests
Zeitpkt
Vorteil
Berechnung der Anzahl der
möglichen Vergleiche bei
mehreren Stichproben
Effektstärke der Anova
Bezeichnung der aufgeklärten
Varianz bei der Anova
Formeln und df der
einfaktoriellen
Varianzananlyse
Kontraste:
a priori; strukt. ,
hypothesengel. Vorgehen
teststark, da keine alpha –
Adjustierung wg. der
Unabhängigkeit d. K
Nachteil begr. Anzahl von
Mittelwertsvergleichen , bei p
Gruppen p-1 mögliche
Kontraste
weniger teststark, da alphaAdjustierung wg. abhängigen posthoc tests,
Bed.:
lässt nur paarweise MW Vergleiche
zu
Gewichte in jd. Zeile
addieren sich zu 0,
paarweise Unabhängigkeit,
PSIdach ^
(p)
m = (2) = p! / 2! (p-2)! bei 4 Gruppen: 1x2x3x4 / 1x2 (4-2)! = 6
bei signifikantem Ergebnis, stellt sich die Frage nach der Effektstärke:

H1: es besteht ein bedeutsamer Zusammenhang zwischen uV und aV (uV
erklärt bedingten Anteil der Varianz der aV)

Anteil aufgeklärter Varianz R2 kann als Maß für die Effektstärke interpretiert
werden (auch Effektvarianz genannt)
Eta2 2 = R2 = SSbetween / SStotal
auch aus F-Wert berechnet: Eta2 = F(p-1) / F(p-1) + (N-p) (p = Anzahl der Gr.
und N= Anzahl der Vp)

die errechnete Varianz Eta2 überschätzt den Effekt in der Population

korrigiertes R2 (Schrumpfungskorrektur) = Omega dach
n
p
SStotal =   (yij – yquer)2
i=1 j = 1
n
SSbetween =  (yquerj – yquer)2
n
j=1
p
SSwithin =   (yij – yquerj)2
i=1 j = 1
Zusammenfassung Anova
Zusammenfassung
Varianzanalyse
Tukey, Scheffé:
post-hoc formuliert; exploratives
Vorgehen zum Generieren neuer
Hypothesen
uneingeschränkte Anzahl von
Mittelwertsvergleichen
N:
n:
Anzahl Probanden
Anzahl Probanden in jeder Zelle
des Versuchsplans
p:
Anzahl der Stufen des Faktors
SS sind additiv
df sind additiv
MS / Varianzen sind nicht additiv!!!!
dftotal = N – 1 bzw. n x p -1
dfbetween = p – 1
dfwithin= N – p
MS = SS / df (für alle SS)
Femp = MSbetween / MS within
Voraussetzungen:

intervallskalierte aV und normalverteilt

homogene Varianzen

n > 20 (schauen, ob vollständig gekreuzt-alle Zellen besetzt und
balanciert

nmax / nmin < 1,5
Gruppenvergleiche nach signifikantem F-Test:

Gruppenunterschied bedeutsam, wenn d > Tukey´s HSD
Anteil aufgklärte Varianz R2: Effektstärkenmaß:
H1: es besteht ein bedeutsamer Zusammenhang zwischen uV und aV bzw. Die
uV erklärt einen bedeutsamen Anteil der Varianz der aV

unkorrigiertes 2 = R2 = SSbetween / SStotal (aufgeklärter
Varianzanteil)

Korrigiert: ^ = Omega dach (Schrumpfungskorrektur)
Erwartungswerte:

s2 zwischen schätzt 2 Effekt + 2 Fehler


s2 zwischen schätzt 2 Fehler
mit Hilfe der Anova werden bei mehr als 2 Stichproben die Mittelwerte auf
Signifikanz überprüft (mit F-Test)
durch Effektcodierung werden Mittelwertsunterschiede der Gruppen
bestimmt
wichtigste Grundlage: die Quadratsummenzerlegung: über SS wird mit
Hilfe der df die jeweilige Varianz berechnet
feste Effekte: wenn alle Stufen des Faktors(uV) realisiert werden
(diskret Variablen wie Geschlecht, Wohnort)


Feste und Zufallseffekte Def. 
Seite 4 von 11
Statistik II
Karin Pilz

Unterschiede feste /
Zufallseff.
Zweifaktorielle
Varianzanalyse
Darstellung der Mittelwerte
Haupteffekt A
Haupteffekt B
Zelleneffekt
Interaktionseffekt
Beispiel Interaktion:
Strukturgleichung 2-faktoriell
Quadratsummenzerlegung
Hypothesen bei 2-faktoriell
Zufallseffekte: uV hat keine festen Abstufungen (kontinuierliche
Variablen wie Extraversion, Alter, Alkoholkonsum)

Beispiel: Alter und Klausurerfolg

bei der einfaktoriellen Anova gibt es keinen Unterschied zur Analyse
mit festen Effekten
feste Effeke:
Zufallseffekte:

einige Stufen werden aus vielen

alle möglichen/interessierenden
möglichen Stufen ausgesucht
Stufen e. Faktors werden realisiert

keine Generalisierung auf nicht

Generalisierbarkeit ist gegeben
realisierte Stufen

Summe der Effekt ist Null

Summe der Effekte muss nicht
0 sein

Ho: alle Effekte sind 0 (j = 0, für

Ho: Varianz der Effekte ist 0
alle j)
(2 = 0)

bei mehreren nominalskalierten uVs und einer intervallskalierten aV --mehrfaktorielle Varianzanalyse (aber nij > 20)

berechnet werden können Haupteffekte und Interaktionseffekte

Interaktionseffekt gibt an, ob die einzelnen Bedingungskombinationen
über den Einfluss der Haupteffekte hinaus spezifische Effekte haben

auch für Interaktionseffekt kann SS berechnet werden, daher hier auch Ftest möglich

Interaktionen: ordinal, disordinal, hybrid
B1 Strukt B2 bildhaft
B3 emotional Randmittelwerte
k=1
k=2
k=3
A1: m. j=1 yq11 = 5
yq12 = 10
yq13 = 12
yq1. = 9
A2: w. j=2 yq21 = 6
yq22 = 11
yq33 = 13
yq2. = 10
yq.1 = 5,5 yq.2 = 10,5
yq.3 = 12,5
yq.. = 9,5(Gesamt
MW)
Zellen- und Randmittelwerte

aj = yqj. – yq.. ; a1 = yq1. – yq.. = -0,5 ; a2 = yq2. – yq.. = +0,5

Summe der Effekt ist Null wie bei einfaktoriell

bj = yq.k – yq.. ; b1 = yq.1 – yq.. = -4 ; b2 = yq.2 – yq.. = 1; b3 = yq.3 – yq.. = 3

Summe der Effekte gleich Null
eine Kombination bestimmter Stufen der Faktoren A und B:

{ab}jk = yqjk – yq.. ; z.B. {ab}11 = 5-9,5 = -4,5 ....

Summe der Effekte ist gleich Null

Zelleneffekt nicht aussagekräftig, da von Haupteffekten beeinflusst

gibt die Wirkung der Kombination bestimmter Faktorstufen über die
Haupteffekte hinaus an

Differenz der Zelleneffekte und der beteiligten Haupteffekte:

(ab)jk = {ab}jk – aj – bk

= (yqjk – yq..) – (yqj. – yq..) – (yq.k – yq..)

= yqjk - yqj. - yq.k + yq..

Summe der Effekte ist gleich Null
2 Medikamente (M1 und M2), getestet an Männern und Frauen

es gibt keinen Unterschied zwischen den Geschlechtern und Medikamenten

aber Wechselwirkung: bei Fr. wirkt M1 gut, M2 kaum; bei Männern
entgegengesetzt
yijk = yq.. + aj +
bk
+ (ab)jk
+ eijk
yq.. + (yqj. – yq..) + (yq.k – yq..) + ( yqjk - yqj. - yq.k + yq..) + eijk
für jede VP kann man den einzelnen wert schätzen, also rückwärts gehen, denn
nur mit Fehler hat man den genauen Wert

F-Test bei Haupteffekten und Interaktionseffekten berechnen:
SStotal = SSFaktorA + SSFaktorB + SSAxB + SSwithin
es gibt 3 Nullhypothesen:

Ho für Faktor A: j = 0 für alle j oder: Randmittelwerte: 1. = u2.=...= p.

Ho für Faktor B: k = 0 für alle k oder .1 = .2=...= .q

Ho für AxB: ()jk = 0 für alle jk (Kombinationen) oder
jk = j.+ .k - ..
ZellenMW = MWj + MWk - GesamtMW
Interaktionsformen

ordinale Interaktion: beide Haupteffekte sind global(über alle Stufen
hinweg) interpretierbar
Diagramm: der gleiche „Trend“ für beide Linien in beiden Diagrammen zu
sehen ist (geordnet)
Seite 5 von 11
Statistik II
Karin Pilz



Formeln 2-faktoriell
hybride Interaktion: nur einer der beiden Haupteffekte ist global
interpretierbar; Diagramm: in einem Diagr. gleicher Trend und im anderen
entgegengesetzter Trend
disordinale Interaktion: Keiner der beiden Haupteffekte ist
interpretierbar ; Diagramm: unterschiedliche Trends für beide Linien in
beiden Diagrammen (ungeordnet)
keine Interaktion: wenn Linien im Diagramm parallel laufen
n p q
SStotal =   (yijk – yq..)2
i=1 j=1 k=1
dftotal = N-1 bzw. n x p x q - 1
p
SSA =  nj (yj.– yq..)2
j=1
dfA = p -1
N : Anzahl Probanden
n: Anzahl Probanden in jeder Zelle
des Versuchsplans
p: Anzahl der Stufen des Faktors A
q: Anzahl der Stufen des Faktors B
p
SSB =  nk(y.k – yq..)2
k=1
dfB = q - 1
p
q
SSAxB =   njk(yqjk - yqj. - yq.k + yq..)2
j=1 k=1
dfAxB = (p - 1) ( q - 1)
n jk p q
SSwithin =   (yijk – yqjk)2
i=1 j=1 k=1
Interpretation am besten mit
Diagramm
MS = SS / df
Femp = MSbetween / MS within
Faktor A
Faktor B
Faktor AxB
A fest,
F= MSFaktorA /
F= MSFaktorB /
F= MSFaktorAxB /
B fest
MSwihtin
MSwithin
MSwithin
A zufällig
F= MSFaktorA /
F= MSFaktorB /
F= MSFaktorAxB /
B zufällig
MSFaktorAxB
MSFaktorAxB
MSwithin
A fest
F= MSFaktorA /
F= MSFaktorB /
F= MSFaktorAxB /
B zufällig
MSFaktorAxB
MSwithin
MSwithin
Anova mit Messwiederholung

Verwendung: um zentrale Tendenz der aV unter mehreren
Verwendung
Experimentalbed. oder Messzeitpunkten zu analysieren

einfaktorielle Varianzanalyse mit Messwiederholung kann als 2-faktorielle
Anova mit gemischten Effekten betrachtet werden:

Faktor A: Messzeitpunkt (fester Effekt)

Faktor B: Versuchsperson ( Zufallseffekt) wir betrachten hier die Person
als eigenen Faktor mit verschiedenen Stufen zu den versch.
Messzeitpunkten

es geht hier nicht um die Unterschiede zwischen den Personen
Beispiele:

Messwiederholung im engeren Sinn: die gleiche aV wird mehrfach
erhoben (Veränderungsmessung)

eine aV wird durch unterschiedliche Verfahren (z.B. untersch. Tests) --Vergleich der Verfahren

Personen aus 2 oder mehr Stichproben werden einander zugeordnet
(Partner, Geschwister)
Vorteile Messwiederholung

ökonomisch: weniger Versuchspersonen, da dieselben Vps mehrfach
getestet

höhere Teststärke, da Fehlervarianz verringert wird (die Varianz
zwischen Vpn ist eliminiert, da man die Vpn nur mit sich selbst vergleicht
Nachteile Messwiederholung Sphärizitätsannahme (Zirkularitätsannahme):

Varianzen und Kovarianzen unter den einzelnen Faktorstufen müssen
homogen sein (vorher / nachher) sonst zu liberale Testung, bei Verletzung
über Korrektur der df berichtigt (Greenhouse-Geiser)
Sequenzeffekte:

Reihenfolge der Testung kann Einfluss haben (Versuchsplanung)
Fehlende Daten zu einem Messzeitpunkt:

führen zu Ausschluss des gesamten Datensatzes zu allen
Messzeitpunkten
Prüfvarianzen der 2faktoriellen Anova
Seite 6 von 11
Statistik II
Quadratsummenzerlegung
Strukturgleichung
Nullhypothese
Formeln Anova
Messwiederholung
Karin Pilz

Drop-out
Testbatterie: Konzentration lässt nach
SStotal = SSbetween +
SSwithin
SStotal = SSbetween +
SStreatment
+
SSerror
(interessiert nicht) (HE Zeitpunktsunterschied) (Fehlervarianz)
(SStotal =
SSbetween subj. + SSwithin subjects)
(SStotal =
SSbetween subj + SSfaktorA/treatment + SSresidual)
( z.B. Persunter Zeitpktuntersch. HE Fehlervarianz)
( HE erkl. Var.
erkl. Var
nicht erklärbar)
yij = yq + aj + pi + eij
aj: fester Effekt des Zeitpunkts
pi: Zufallseffekt der VPi
eij: Fehler
Ho: j = 0 für alle j, keine Effekte des Messzeitpunkts, keine
Mittelwertsunterschiede
p
SStreatment =  n(yq.j – yq..)2 (wie bei Haupteffekt)
j=1
dftreatment = p - 1
n
p
SSerror =  (yqjk - yqj. - yq.k + yq..)2 (Interaktionstherm)
i=1 j=1
dferror = (p –1) (N-1) bzw. (p – 1) (q – 1)
Femp = MStreatment / MSerror
Anova mit
Messwiederholung
Zusammenfassung





Kovarianzanalyse
Residualisierung
Wann, warum, Interpretation
Störvariable
Voraussetzungen
Kovarianzanalyse Berechnung
Effektgröße
Konventionen müssen
gelernt werden
Durchführung von Anova mit Messwiederholung, wenn gleiche aV
mehrmals erhoben wurde
sehr ökonimisch, weil weniger VPs, dadurch höhere Teststärke
Sphärizitätsannahme muss erfüllt sein, sonst Anova zu liberal (zu oft wird
H1 angenommen) --- durch Korrektur der df berichtigen (GreenhouseGeiser)
F-Test vergleicht die Varianz des Treatments mit der Fehlervarianz
innerhalb der Gruppen, d.h. Fehlervarianz der VPn wird nicht berücksichtigt
Vorteil der Messwiederholung auf Verringerung der Fehlervarianz im FBruch


Residualisierung: eine Regression der aV wird auf die Kovariate
berechnet. Anschließend werden für alle Vp die Diff der tatsächl. y-Werte
und der vorhergesagten y-Werte gebildet

ein Verfahren, das eine Varianzanalyse mit einer Regressionsanalyse
kombiniert

wird eingesetzt, um Fehlervarianz zu verringern und damit Power zu
erhöhen

Variablen, die nichts mit der inhaltlichen Hypothese zu tun haben, aber
dennoch aV beeinflussen

Beispiel: Temperatur im Untersuchungsraum beeinflusst
Konzentrationsleistung

Kontrolle der Störvariablen durch:

Konstanthalten (Beleuchtung)

Aufnahme als Faktor in Versuchsplan ( Geschlecht)
unökonomisch, weil man sonst zu viele Vps benötigt

Störvariable als Kovariate verwenden (statistische Kontrolle)

(Linearer Zusammenhang)

Varianzhomogenität, intervallskaliert, Normalverteilung

Homogene Regressionskoeffizienten, b-Gewichte dürfen sich nicht
signifikant unterscheiden

Quadratsummenzerlegung von Kovariate und aV

Produktsummenzerlegung

Entfernen der Varianz der Kovariate: Berechnen der Modifizierten SS

F-Test

Kontrolle der Fehlervarianzreduktion R2 within

signifikanter Unterschied in Stichproben

„praktische“ Bedeutsamkeit eines Effekts abzuschätzen
es gilt:

Je größer der Unterschied zwischen den experimentellen Bedingungen,
desto größer die Effektstärke

Je kleiner die Varianz innerhalb der Bedingungen, desto größer die
Seite 7 von 11
Statistik II
Distanzmaß delta
Effektgröße Varianzquotient
Phi2
Wann wird Phi2 größer?
Effektgröße Varianzquotient
Omega2
Alpha- und Beta Fehler
Wahrscheinlichkeiten von
oben
Alpha – Fehler
Beta – Fehler
Alpha- und Beta – Fehler
Teststärke
Wechselseitige
Abhängigkeit der 4 Größen
(Effekt, N, alpha, beta)
Einflussgrößen auf Teststärke
Beta reduzieren
Karin Pilz
Effektstärke
mögliche Darstellungen:

als Distanzmaß zw. Populationsmittelwerten

Varianzquotient
 kann nur bei p = 2 Gruppen eingesetzt werden

Abstand der Mittelwerte normiert an der Streuung

Stichprobeneffekt schätzt Populationseffekt

d umso größer, je größer der Abstand der Mittelwerte

d umso größer mit kleinerer Streuung
 = 1 – 2 /  in Pop
^ = d = yq1 – yq2 / ^
^ = S1 + S2 / 2
z.B. d = 2.21 bedeutet: 2.21 Streuungseinheiten entfernt----großer Effekt nach
Cohen

Varianzquotient Phi ist Verhältnis von systematischer (erklärter) zu
unsystematischer (nicht erklärter) Varianz

2 = 2Treatment / 2 error

geschätzt: 2^ = f2 = t2-1 / N

Phi schwierig zu interpretieren

mit gr. systematischer Varianz

mit geringerer Fehlervarianz

Anteil der erklärten Varianz zur Gesamtvarianz (r2)

2 = 2 Treatment / 2 total

= 2 Treatment / 2error + 2 Treatment
Omega wird größer

je größer Varianz zwischen den Bedingungen (Effektvarianz)

je kleiner Varianz innerhalbe der Gruppen (Fehlervarianz)

wie die MS keine erwartungstreuen Schätzer auf die Population sind, muss
auch hier korrigiert werden -----Omega dach
in der Stichprobe
in der Population gilt
Ho gilt
H1 gilt
Ho wird angenommen
1–

H1 wird angenommen

1-

Ho gilt und wird angenommen: p(n.s./Ho) = 0.95

Wahrscheinlichkeit, dass H1 angenommen wird, obwohl in Population Ho
gilt: p(s / Ho) = 0,05

H1 wird angenommen, obwohl H1 falsch ist

ein zufällig gefundener Unterschied wird signifikant, obwohl in Pop kein
Unterschied besteht

Größe des alpha-Fehlers wird vorher festgelegt (bei  = 0.05 besteht die
Möglichkeit, das bei 100 gezogenen Stichproben aus der Pop im Schnitt 5
Stichproben rechts von Tkrit liegen --- in 5% der Fälle ist die Annahme die
Stichprobe gehört zu einer anderen Population falsch, weil der Wert wie
oben beschrieben zufällig zustande kam, die Ho wird fälschlicherweise
verworfen)

jeder Wert, der kleiner als tkrit ist , führt zur Beibehaltung der Ho, es wird
angenommen, der Wert stammt aus der Ho Population

der Wert könnte aber aus einer Alternativpopulation stammen (Beta-Fehler)

Ho wird beibehalten, obwohl sie falsch ist

reduziert man Wahrscheinlichkeit für Alpha-Fehler, wächst die
Wahrscheinlichkeit für den Beta-Fehler

P = 1 -  (wie groß ist die Chance einen Effekt zu finden?)

Gegenwahrscheinlichkeit zum Beta-Fehler

Wahrscheinlichkeit einen bestehenden Unterschied nachzuweisen

bei geringer Power, ist die Wahrscheinlichkeit hoch, einen existierenden
Effekt zu übersehen hoch

wenn Power unbekannt, kann H1 folglich nicht endgültig verworfen werden,
umgekehrt bedeutet ein signifikantes Ergebnis, dass H1 mit
Fehlerwahrscheinlichkeit von alpha gilt, hier eindeutigere Interpretation
möglich

je kleiner beta, desto höher Power

je kleiner alpha, desto größer beta, desto kleiner Power

je höher Effektstärke (Distanzmaß), desto kleiner beta, desto größer Power

höheres alpha-Niveau wählen

einseitig testen
Seite 8 von 11
Statistik II
Karin Pilz

Stichprobenumfang und
Teststärke
Teststärkenanalyse
Faktorenanalyse
Anwendung der
Faktorenanalyse
Voraussetzung
Faktorenanalyse
Mathematisches Vorgehen
Fundamentaltheorem
Faktorladungen
Kommunalität (h)
Kommunalitätsproblem
Streuung des Merkmals reduzieren (z.B. durch Entfernen von
Ausreißern,.Störvariablen eliminieren), geringere Überlappung, dadurch
sinkt die Wahrscheinlichkeit für statistischen Fehler

Stichprobe vergrößern (Standardfehler verringert, df hoch, tkrit wird
geringer

Effektstärke vergrößern(MW der Pop. liegen nah beieinander: kl. Effekt,
großer Beta - Fehler

abhängige Stichproben verwenden (Messwiederholung, t-test f. abh.,
reduzieren der Fehlervarianz)

teststarke Verfahren wählen (parametrische Tests verwenden, wenn
Voraussetzung hierfür erfüllt sind)

je größer Stichprobenumfang, desto kleiner beta, desto gr. Teststärke, desto
eher wahrscheinlich ein signifikantes Ergebnis zu finden, bei sehr hoher fast
immer ----mit steigendem N verringert sich Fehlervarianz und jede Ho
kann mit ausreichend großen N verworfen werden -----Lösung:
Effektstärke vorher festlegen

je kleiner Stichprobe, desto geringere Power, desto schwieriger Effekt zu
finden

a priori Teststärkenanalyse: Festlegen von Effekt, alpha, beta ;
Berechnen von N

post-hoc-Teststärkenananlyse: Festlegen: alpha, Effekt, N;
Berechnen von beta

Kompromissanalyse

multivariates Verfahren, d.h. es werden mehrere aVs parallel untersucht

Ziel: Vereinfachung eines komplexen Datensatzes (Reduktion)

viele Variablen werden zu wenigen Faktoren zusammengefasst

„Items“ (manifeste Variablen) laden auf einen Faktor (latente Variablen)

Ziel: Konstruktion / Strukturierung und Überprüfung/ Interpretation und
Auswertung von Fragebögen

Items zu einem psychologischen Konstrukt werden formuliert

explorative Faktorenanalyse: Bildung von Subskalen (Items, die Ähnliches
messen, werden zu Faktor zusammengefasst)

(konfirmatorische Faktorenanalyse:es kann eine auf theoretischer Ebene)
(begründete Skalenstruktur überprüft werden (Strukturgleichungsmodelle,)
(AMOS)

es werden mehrere Variablen p für Faktorenanalyse benötigt, wobei für
jede Person der Wert auf jeder Variable bekannt sein muss (jedes Item
muss beantwortet werden – wie bei Messwiederholung)

Intervallskalenniveau

Normalverteilung der Variablen

Anzahl Vpn: N >= 3 x p (Richtwert)

es werden nur lineare Zusammenhänge abgebildet
1.Matrix der Variablenwerte X Nxp
2.Matrix der standardisierten Werte: Z Nxp ( Spalten: Mittelwert = 0  =1)
3.Korrelationsmatrix: R pxp
Kommunalitätsproblem (Iterative Abschätzung)
4.Reduzierte Korrelationsmatrix: hRpxp
Extraktionsproblem (wie viele Faktoren werden ausgewählt)
5.Faktorladungsmatrix: A pxq
N : Vpn
Rotationsproblem(iterative Absch.)
p : Variabllen
6. Rotierte Faktorladungsmatrix: A`pxq
q : Faktoren
Faktorwerteproblem
Iterative Abschätzung
7.Faktorwertematrix: FNxq
besagt, dass sich jeder der standardisierten Werte als Linearkombination der
Faktorwerte und Faktorladungen beschreiben lässt
Korrelation der Faktorwerte mit Ausgangswerten in Variablen ( Person, die
hohe Werte in Variable hat, hat auch hohe Werte auf x und umgekehrt)

hohe Korrelation von x und Lamda

Korrelation eines Faktors und einer Variablen hängt vom Winkel ab

r = cos() –----  = 0° = r = 1 ; 90° = r = 0

die insgesamt durch alle Faktoren aufgeklärte Varianz dieser Variablen

Variable nimmt immer Werte zwischen 0 und 1 an

wird aus Zeilensumme in der Matrix der Determinationskoeffizienten
berechnet

h2 = 1, wenn p = q

Kommunalitätsproblem:
Seite 9 von 11
Statistik II
Karin Pilz

Eigenwert ()
Extraktionsproblem
Rotationsproblem
unterschiedliche
Rotationsverfahren:
Wie viel Varianz von jeder Variablen wird zu Beginn der FA aufgeklärt, also
bevor die endgültige Lage der Faktoren bekannt ist?
Hauptkomponentenanalyse (PCA): (von Bortz empfohlen)

zu Beginn des Optimierungsprozesses wird eine Kommunalität von 1
angenommen

Vorteil: insgesamt aufgeklärte Varianz wird optimiert

es kann Faktoren geben, die nur auf einer Variable hochlädt
Hauptachsenanalyse: (von Leonhart empfohlen)

zu Beginn des Optimierungsprozesses wird die Kommunalität für jede
Variable geschätzt

es werden Faktoren bevorzugt, auf denen viele Variablen laden
Art der Analyse wirkt sich auf die adjustierte Korrelationsmatrix und alle
folgenden Schritte aus

Eigenwert eines Faktors gibt an, wie viel Varianz der Faktor an allen
Variablen aufklärt

wird aus Spaltensumme der Matrix der Determinationskoeffizienten
berechnet

Wertebereich abhängig von Anzahl der Variablen, daherWerte > 1

Eigenwert 1 bedeutet, dass ein Faktor insgesamt so viel Varianz aufklärt,
wie eine der standardisierten Variablen aufweist

je größer Eigenwert, desto besser ist der Faktor

Selektionsstrategie, besteht darin alle Faktoren  > 1 zu akzeptieren

zur Berechnung der FA werden genau so viele Faktoren wie Variablen
berechnet

Um Ziel der Datenreduktion zu erreichen, später weglassen der
Faktoren, die wenig Varianz aufklären
Unterschiedliche Kriterien:

Kaiser-Gutman-Regel(nur Faktoren mit Eigenwert >1 berücksichtigt –
Varianzanteil einer Variablen, Voraussetzungen: N > 5xp

Kriterium der extrahierten Varianz (es wird festgelegt, wie viel Varianz
aufgeklärt werden soll – keine Begründung welcher Varianzanteil gewählt
wird)
Vorgehen:

Faktoren nach Eigenwerten sortieren

alle werden aufsummiert ----Summe  = p

für jeden Eigenwert wird der Anteil aufgeklärter Varianz als  / p
berechnet

alle Kriterien werden berücksichtigt, bis kumulierte Varianz das
Kriterium übertrifft

Screetest (graphische Methode, um sinnvolle Anzahl der Faktoren zu
bestimmen: Eigenwerte der Faktoren als Graphik dargestellt, bevor Graph
eine Ebene erreicht ---Problem: oft nicht eindeutig)

Theoriegleitetes Vorgehen ( in SPSS direkt die Anzahl der Faktoren
eingeben, dadurch Möglichkeit verschiedene Lösungen auszuprobieren,
inhaltliche Lösung zu finden – Bspl. Intelligenztest: räuml., mathem, sprachl
Intelligenz---dabei wird überprüft, ob Items auf Faktoren laden

erst wird die Position der Faktoren so gewählt, dass sie jeweils soviel
Varianz wie möglich aufklären

wenn die Zahl und Lage der Faktoren bestimmt ist, können die Achsen
um den Koordinatenursprung rotiert werden – es gehen keine
Informationen verloren

Faktorladungen ändern sich durch Rotation

Ziel: Rotation ist Einfachstruktur, d.h. jeder Faktor soll auf einigen
Variablen sehr hoch und auf anderen sehr gering laden

dadurch Faktoren leichter inhaltlich zu interpretieren
orthogonale Rotation:
oblique Rotation:

Faktoren bleiben unabhängig, sie 
„schiefwinklige“ Zusammenhänge
stehen senkrecht aufeinander
zwischen Faktoren erlaubt

Vorteil: durch Unabhängigkeit,

Vorteil: Möglichkeit, Faktoren
maximale Vereinfachung der
höher Ordnung zu bestimmen
Daten
(Beispiel: Intelligenztests 100
Items auf 8 Aufg.typen, laden auf

bekanntestes Verfahren:
3 Faktoren, diese auf
„Varimax“ – Methode
Generalfaktor

Spaltensummen der quadrierten
bekanntestes Verfahren:
Faktorladungsmatrix maximiert 
„oblimin“ – Methode
Seite 10 von 11
Statistik II
Ergebnis der Faktorenanalyse
abhängig von:
FA Zusammenfassung
Interpretation SPPS Ausgabe
FA Zusammenfassung
Karin Pilz

Stichprobe

Auswahl der Items

der gewählten Verfahren der FA

Auswahl der Faktoren

Rotation
die gefundene Faktorenstruktur sollte nur als Hypothese betrachtet werden
Ablauf

Jede Vp ist durch Vektor der Werte auf p z-standardisierten Variablen
gekennzeichnet

Stichprobe bildet eine Punktewolke im p-dimensionalen Raum

Achsendrehung, so dass sie maximale Varianz aufklären

Achsen weglassen, die wenig Varianz aufklären ( > 1)

verbleibenden Achsen definieren einen (eingeschränkten) Parameterraum.
Dieser ändert sich nicht, wenn Achsen nun erneut gedreht werden, um
Einfachstruktur zu erreichen
Entscheidungen für die Berechnung:

Berechnungsverfahren:

Hauptkomponenten - Analyse

Hauptachsen – Analyse

Anzahl der Faktoren:

Kaiser-Gutman-Kriterium

Screetest

hypothesengeleitetes Vorgehen

Art der Rotation:

orthogonal (Varimax)

oblique (Oblimin)
Seite 11 von 11