Die Wahrscheinlichkeitsrechnung

Idlhammer Markus
1
Idlhammer Markus
Die Wahrscheinlichkeitsrechnung
1 Historisches zur Wahrscheinlichkeitsrechnung
Ein Freund von Blaise Pascal (1623 – 1662), Chevalier de Mére´ (1607 – 1684) beschäftigte sich
hauptberuflich mit dem Würfelspiel. Die Bank (de Mére´) gewann immer dann, wenn ein Spieler
bei vier Würfen mit je einem Würfel wenigstens eine Sechs warf. Die Grundlage dieser Regeln
führten dazu, dass Herr de Mére´ sehr reich wurde.
Um noch mehr Geld zu verdienen, änderte er die Regeln etwas ab. Die Bank gewann nun, wenn
ein Spieler bei 24 Würfen wenigstens eine doppelte Sechs würfelte. Ab diesem Zeitpunkt verlor
de Mére´ fast sein ganzes Vermögen. Worauf dies basiert, wird in weiterer Folge noch
beschrieben.
2 Grundbegriffe der Wahrscheinlichkeitsrechnung
2.1 Das Zufallsexperiment ist ein Vorgang:




der nach bestimmten Vorschriften ausgeführt wird
der beliebig oft wiederholbar ist
bei dem das Ergebnis vom Zufall abhängt
bei welchem die Ergebnisse bei mehrfacher Durchführung voneinander unabhängig
sind
Beispiel: Werfen eines Würfels:
2.2 Elementarereignis:
Jedes Zufallsexperiment besitzt eine Reihe möglicher elementarer Ereignisse mit der
Eigenschaft dass immer nur ein bestimmtes Ereignis auftreten kann.
Beispiel: Zufallsexperiment: Werfen eines Würfels (sechs mögliche Elementarereignisse
[1…..6])
Ereignisraum:
Besitzt ein Zufallsexperiment n- mögliche Elementarereignisse (e1, …., en), dann bildet die
Menge {e1,…….,en} den Ereignisraum E.
E = {e1,…….,en}
Der Ereignisraum kann endlich oder unendlich sein.
Beispiel 1:
 Werfen eines Würfels
 Das einmalige Werfen einer Münze
 Zweimaliges Werfen einer Münze
E = {1, 2, 3, 4, 5, 6}
E = {Zahl, Kopf}
E = {KK, KZ, ZK, ZZ}
Ergebnis:
Teilmenge von E; E = {1, 2, 3, 4, 5, 6}
Ergebnis: gerade Zahl = {2, 4, 6}
2
Idlhammer Markus
2.2.1 Mögliche Operationen mit Ereignissen
Vereinigung zweier Ergebnisse
A:
= {1,2}
B: = {3}  A  B = {1,2,3}
VENN-Diagramm:
E
A
B
1,2
3
Vereinigung zweier Ergebnisse
A: = {1,2,3}
B: = {2,3,4}  A  B = {2,3}
E
A
B
1
4
2
3
Zwei Ergebnisse sind disjunkt, wenn sie einander
ausschließen!
A  B = {} = Ø
 leere Menge
= unmögliches Ereignis
E
A
B
Zwei Ereignisse (A und A )sind komplementär
wenn A  A = E (sicheres Ereignis) und
wenn A  A = Ø (unsicheres Ereignis)
E
A
A
3
Idlhammer Markus
Beispiel 2:
Zufallsexperiment: 2 mal würfeln
E=
{(1,1); (1,2); (1,3); (1,4); (1,5); (1,6);
(2,1); (2,2); (2,3); (2,4); (2,5); (2,6);
….
….
(6,1); ….
….. (6,6)}
A: Beim ersten Wurf eine „6“
B: Beim zweiten Wurf eine „6“
A  B = { (1,6); (2,6); (3,6); (4,6); (5,6); (6,6); (6,1); (6,2); (6,3); (6,4); (6,5)}  11
Elementareeignisse
A  B = {(6,6)}  1 Elementarereignis
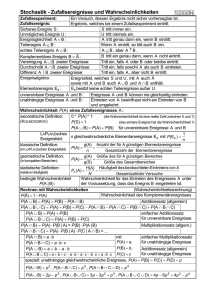
2.3 Wahrscheinlichkeit
Die Wahrscheinlichkeit ist ein Maß das zur Quantifizierung der Sicherheit bzw. Unsicherheit des
Eintretens eines bestimmten Ereignisses dient, das im Rahmen eines Zufallsexperimentes abläuft.
2.3.1 Der klassische Wahrscheinlichkeitsbegriff
Abb. 2: klassische „Zufallsgeräte“ nach P. S. Laplace
P(E) =
Abb.1: Pierre Simon Laplace 1749-1827
aus www.mathematik.de
Zahl der günstigen Fälle
[E]
=
[] Zahl der möglichen Fälle
Beispiele3 und 4:
(a)
A: Gerade Zahl bei einem Wurf eines Würfels
Zahl der günstigen Fälle:
3
Zahl aller möglichen Fälle:
6
4
Idlhammer Markus
P(A) =
3
= 0,5  (50%)
6
(b)
W: Morgen ist gutes Wetter!
E = {W; W }
P(W) = ½ = 0,5 = 50%
Der klassische Wahrscheinlichkeitsbegriff funktioniert in diesem Fall nicht, da im Winter eine
höhere Regenwahrscheinlichkeit existiert als im Sommer!
2.4 Statistischer Wahrscheinlichkteitsbegriff nach (R. v. Mises)
Voraussetzung: Zufallsexperiment
Beispiel: Münzwurf n: 1 000 000
P(Kopf) =
Häufigkeit von Kopf
n
lim
n
P(A) = lim n 
h( A)
= lim n  f (A)
n
Abb.3: R. v. Mises 1883 - 1953
aus www.mathematik.de
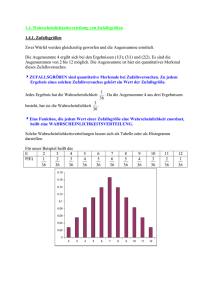
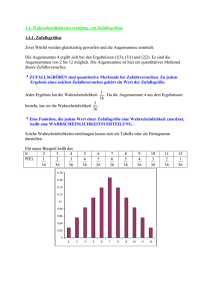
NOETHER (1971) hat Münzwürfe durchgeführt

h(Kopf)
F(Kopf)
10
7 0,7
100
47 0,47
1000
492 0,492
5000
2515 0,503
f(Kopf)
n
0,5
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
10
100
1000
5000
n
5
Idlhammer Markus
2.5 Kolmogorov (Axiomatischer Wahrscheinlichkeitsbegriff)
Axiom: Ein Grundsatz den man nicht mehr beweisen muss
(z. B. 1 + 2 = 3)
1. Axiom:
Nichtnegativität (0  P(A)  1)
2. Axiom:
Normierung
P(E) = 1
3. Axiom:
Additivität
= Kolomogrov 3
Sind 2 Ereignisse A und B disjunkt so gilt:
P(A  B) = P(A) + P(B)
Abb.4: Andrej N. Kolomoforov
1903-1987
Erweiterung auf mehr als 2 disjunktive Ereignisse:
aus: www.mesure.igpp.ucla.edu/solarterrestrial-luminaries/timeline.html
Ai  Aj = {}
 P(A1  A2  A3…  An) = P(A1) + P(A2) + P(A3) + P(An)
Beispiel 5:
Zufallsexperiment:
Ereignis A:
P(A) = ?
E=
Wurf von zwei Würfeln
Augensumme beider Würfel ist „4“
{(1,1); (1,2); (1,3); (1,4); (1,5); (1,6);
(2,1); (2,2); (2,3); (2,4); (2,5); (2,6);
….
….
(6,1); ….
….. (6,6)}
Voraussetzung:
Die Würfel sind fair!
36 gleichwahrscheinliche Elementarereignisse!
P(Elementarereignisse) = 1/36
A:= { (1,3)  (2,2)  (3,1) }
P(A) = P(1,3) + P(2,2) + P(3,1)
K[3] (Kolomogrov 3)
P(A) = 1/36 + 1/36 + 1/36 = 3/36 = 1/12 = 8,333%
Komplementärereignis zu A:
A (A  A = E)
6
Idlhammer Markus
P(A) + P( A ) = P€ = 1
P( A ) = 1-P(A) = 1-1/12 = 11/12 = 91,666%
Ein Spezialfall des Additionssatzes:
P(A  B) = P(A) + P(B)  A  B = Ø (A und B sind disjunkt)
2.5.1 AllgemeinerAdditionssatz
E
Herleitung:
Ergebnis:
A
B
A  B A  ( A  B)
Alles was zu Aoder
zu B Gehört
Alle
Ergebnisse
aus A
+
Alle Ergebnisse, die gleichzeitig zu B und zu
denen die nicht in A liegen gehören
P( A  B)  P(A)  P ( A  B)
Allgemeiner Additionssatz der Wahrscheinlichkeitsrechnung:
P( A  B)  P(A)  P( B)  P( A  B)
Kolomogrov = Spezialfall dieses Satzes, da P(A╫B) bei disjunkten Ereignissen Ø ist, somit O:
P( A  B)  P(A)  P ( B)  0
P( A  B)  P(A)  P ( B)
7
Idlhammer Markus
Beispiel 6:
2 ideale Münzen werden geworfen!
Fragestellung: P(mindestens eine Münze zeigt Kopf)= ?
A: 1. Münze zeigt Kopf P(A) = 0,5
B: 2. Münze zeigt Kopf P(B) = 0,5
E
ZZ
Zahl/ Kopf
A
B
Kopf/ Kopf
Kopf/ Zahl
P(A  B) = P(A) + P(B) - P (A  B)
P(A  B) = 0,5 + 0,5 – 0,25
Mindestens eine der
Münzen zeigt Kopf!
Eine von vier Möglichkeiten ist diese:
Kopf/ Kopf
P(A  B) = 0,75
Vierfeldertafel:
A
A
B
P(A  B ) = 0,25
P( A  B ) = 0,25
 = P(B) = 0,5
B
P(A  B ) =0,25
P( A  B ) =0,25
 = P( B ) = 0,5
 = P(A) = 0,5
 = P( A ) = 0,5
P(E) = 1
P(A  B) = P(A  B) + P(A  B ) + P( A  B) = 0,75
8
Idlhammer Markus
Beispiel 7:
Zwei ideale Würfel werden geworfen, wie groß ist die Wahrscheinlichkeit dass;
a) eine Augensumme von 7 zu erreichen
b) eine Augensumme von höchstens 11 zu erhalten?
Ad a)
A: Augensumme = 7
A = {(6,1);(1,6); (5,2); (2,5); (4,3); (3,4)}
P(A) = 6/36 = 1/6 = 0,16666 = 16,66%
Ad b)
Es existieren für dieses Ereignis 35 Möglichkeiten!
B: Augensumme höchstens 11
B : Augensumme = 12
P( B ) = 1/36
P(B) = 1 – 1/36 = 35/ 36 = 0,97222 = 97,22%
Beispiel 8:
Jemand bewirbt sich bei 2 Firmen A und B. Die Wahrscheinlichkeit P dass die Bewerbung bei
der Firma A angenommen wird liegt bei P(A)= 0,5, bei der Firma B liegt sie bei P(B)= 0,6.
Zusätzlich rechnet der Bewerber mit einer Wahrscheinlichkeit P(A  B) = 0,3 dass er von beiden
Firmen angenommen wird.
a) Wie groß ist die Wahrscheinlichkeit dass der Bewerber von mindestens einer der beiden
Firmen eine Zusage erhält?
P(A  B) = P(A) + P(B) – P(A  B) = 0,5 + 0,6 – 0,3 = 0,8 = 80%
b) der Bewerber erhält von höchstens einer Firma eine Zusage:
P( A  B ) = 1 – 0,3 = 0,7 = 70%
2.6 Bedingte Wahrscheinlichkeit
 gilt für zwei Ergebnisse A, B in einem Zufallsversuch:
P(A  B) = P(A) . P(B),
dann sind die beiden Ergebnisse A, B unabhängig.
Beispiel 9:
Nach einem Laplace-Versuch wird eine Zahl aus der Menge {1, 2, 3, …., 36}gezogen und
folgenden Ergebnisse werden untersucht:
A: die gezogene Zahl ist durch 3 teilbar,
B: die gezogene Zahl ist durch 4 teilbar,
C: die gezogene Zahl ist durch 6 teilbar.
9
Idlhammer Markus
Daher gilt:
1
1 1
 P( A  B)  P( A) P( B)  
12
3 4
und
1
1 1
 P( A  C )  P( A) P(C )  
12
4 6
Wie man sieht sind die Ergebnisse A und B voneinander unabhängig  die Teilbarkeit durch 3
begünstigt oder erschwert nicht die Teilbarkeit durch 4. Dagegen sind B, C abhängig was
bedeutet dass die Teilbarkeit durch 4 die Teilbarkeit durch 6 begünstigt.
Die Zahl
P(A/B):=
P( A  B)
P( B)
Nennt man bedingte Wahrscheinlichkeit von A unter der Bedingung B oder von A nach B. Dabei
muss P(B) ≠ 0 sein, was wiederum bedeutet dass B nicht das unmögliche Ergebnis sein darf.
Man deutet P(A/B) als die Wahrscheinlichkeit von A, falls von vornherein nur die Ausfälle von
B in Betracht kommen. Daher gilt:
P(A/B)P(B) = P(A  B) = P(B/A)P(A)
Im Fall P(A) ≠ 0 gilt insbesondere
P(B/A) =
P( A / B) P( B)
P( A)
Formel von Bayes für Wahrscheinlichkeiten:
Genau dann sind A, B unabhängig, wenn
P(A/B) = P(A) bzw. P(B/A) = P(B)
10
Idlhammer Markus
Bedingte Wahrscheinlichkeiten stellt man mit der Hilfe eines Wahrscheinlichkeitsbaums dar:
P(A)
P( A )
A
P(B/A)
A
P(B/ A )
P( B /A)
B
B
P( B / A )
B
B
Beispiel 10:
Aus einem Kartenspiel mit 32 Karten werden drei Karten gezogen. Wir untersuchen die
Ereignisse A: nur „Bilder“ und B: “mindestens zwei Damen“
P(A) =
12 
 
3
 32 
 
3

11
8  31
 4  12   4   28 
        
3 0
2 1
43
P(B) =         
31 40
 32 
 
3
und
weiters:
 4  12   4  12 
        
3 0
2 1
19
P(A  B) =         
31 40
 32 
 
3
Es gilt P(A  B) ≠ P(A) P(B), die Ereignisse A und B sind also abhängig. Daher ist
P(A/B) =
P(B/A) =
19  31 40 19
  0,4418 = 44,18%
31 40  43 43
19  8  31 19
  0,344 = 34,54%
31 40 11 55
11
Idlhammer Markus
Beispiel 11:
Beim Ziehen der Lottozahlen („6 aus 45“) sei Ci das Ereignis, dass die ite gezogene Zahl in einem
bestimmten Tip eine „Richtige“ ist. Dann ist:
V = C1  C2  C3  C4  C5  C6
6 5 4 3 2 1
1
    

45 44 43 42 41 40  45 
 
6
Man nennt die Ereignisse C1, C2, ….Cn  Ω unabhängig, wenn je n – 1 Ereignisse unabhängig sind
und außerdem P(C1, C2, ….Cn) = P(C1)P(C2)…..P(Cn) gilt. Dies bedeutet, dass jede Teilmenge der
Menge der Ereignisse die Wahrscheinlichkeit des „Schnittereignisses“ gleich dem Produkt der
einzelnen Ereignisse sein muss. Die Ereignisse aus dem Beispiel 11 sind nicht unabhängig, denn es
6
gilt P(Ci) =
für i = 1, …, 6.
45
P(V) =
2.7 Zufallsexperiment
Wenn ein Zufallsexperiment mit der (endlichen) Menge Ω der möglichen Ausfälle gegeben ist,
dann nennt man jede Funktion
X : Ω  R
eine Zufallsgröße oder Zufallsvariable auf diesem Zufallsversuch.. Der
Wertebereich einer Zufallsgröße ist in Anwendungssituationen im Regelfall ein Größenbereich,
dessen Elemente „benannte“ Zahlen sind, also z. B. physikalische Dimensionen (cm, kg, …)haben.
Für jede Teilmenge T von R ist {ω є Ω | X (ω) є T}ein Ereignis. Die wichtigsten Beispiele hierfür
sind:
„X = a“
: = {ω є Ω | X (ω) = a}
„X  a“
„a  X  b“
: = {ω є Ω | X (ω)  a }
: = {ω є Ω | a  X (ω)  b}
Man nennt die Funktion
A  P(X = a) die Wahrscheinlichkeitsverteilung von X,
A  P(X  a) die Wahrscheinlichkeitsfunktion von X.
12
Idlhammer Markus
Ist die Wertemenge X(Ω) von X sehr umfangreich, so arbeitet man mit Klassierungen. Die Klasse
zum Intervall xk , xk 1  besteht aus allen Werten x є X(Ω) mit xk < x ≤ xk+1. Man stellt P (xk < X ≤
xk+1) als Rechtecksfläche über dem Intervall dar. Ist Δk := xk+1 – xk und dk die Höhe dieses Rechtecks, dann
gilt:
P (xk < X ≤ xk+1) = dk . Δk
P (xk < X ≤ xk+1)
dk
Δk
xk
xk+1
Die Funktion: d : x  dx für xk < x ≤ xk+1
Heißt Dichtefunkton von X zu der gegebenen Klassierung. Die graphische Darstellung von d nennt
man Histogramm von X zu der gegebenen Klassierung.
Mit der Dichte d lässt sich die Wahrscheinlichkeitsfunktion näherungsweise als Integral
ausdrücken:
P(X) ≤a) ≈
a
 d ( x) dx

Dabei ist die Näherung umso genauer, je gleichmäßiger die Werte von X in den einzelnen Klassen
über das ganze Intervall verteilt sind.
P(X≤a)
d
x
a
Ist X(Ω) sehr umfangreich, so ist die Wahrscheinlichkeitsverteilung nicht sehr nützlich, nur die
Wahrscheinlichkeitsfunktion ist brauchbar.
13
Idlhammer Markus
Wenn X(Ω) = {x1, x2, ….., xk} dann definiert man den Erwartungswert von X als
k
E(X) : =

P(X = xi) . xi
i 1
Die Varianz von X als:
k

V(X) :=
P(X = xi) . (x – E(X))2
i 1
Und die Standardabweichung von X als:
σ (X) := V (X )
Man benützt oft die Abkürzungen:
μ := E(X)
und
σ := σ(X)
Jakob Bernoulli (1654-1705),
Quelle: www.esa.int/images
2.8 Die Binominalverteilung
Ein Zufallsversuch mit genau zwei Ausfällen (Treffer/ Fehlschlag oder +/ -, oder 1/0) heißt
Bernoulli- Versuch (nach Jakob Bernoulli, 1654 – 1705). Man nennt p := P (Treffer) die
Trefferwahrscheinlichkeit; dann ist P (Fehlschlag) = 1 – p. Eine solche n-fache Wiederholung des
Bernoulli-Versuchs heißt Bernoulli-Kette der Länge n. Die Menge der möglichen Ausfälle einer
solchen Bernoulli-Kette ist:
Ω = {1,0}n
Ein Ausfall ist also ein n-Tupel aus 1 und 0. Es gib genau 2n verschiedene Ausfälle.
ein Ausfall:
ω = (0, 0, 1, 0, 1, 1, ….., 0, 1, 1,)
mit genau k Treffern hat die Wahrscheinlichkeit
P(ω) = ω pk(1-p)n-k
Für die auf Ω definierte Zufallsgröße
X = Anzahl der Treffer
gilt:
n
P(X = k) =   pk (1 – p)n-k
k 
14
Idlhammer Markus
n
Denn man kann auf genau   Arten ein n-Tupel aus 1 und 0 bilden, welches genau k-mal 1
k 
enthält.
Beispiel 12:
Zwei Würfel werden gleichzeitig geworfen.
a) Wie groß ist die Wahrscheinlichkeit, bei 3 Würfen jedes Mal einen Pasch zu werfen?
b) Mit welcher Wahrscheinlichkeit erzielt man bei 5 Würfen höchstens einen Pasch?
3
1
a) P =   = 0,0046 = 0,46 %
6
5
4
5
5 1
b)    5      0,8037 = 80,37%
6
6 6
15
Idlhammer Markus
3
Schlusswort
Die Faszination die seit ihren Anfängen von der Wahrscheinlichkeitstheorie ausgeht, liegt in dem
scheinbaren Widerspruch, dass der Zufall Gesetzmäßigkeiten gehorcht. Es bedurfte einer langen
Entwicklung und viele heftige Auseinandersetzungen bis die mathematische Form gefunden
wurde, die uns in die Lage versetzen soll solche Gesetzmäßigkeiten zu formulieren und zu
beweisen. Die in den vorangegangenen Kapitel behandelten Themen sind bei weitem nicht alle
Bereiche aus der Wahrscheinlichkeitstheorie und daher auch nicht vollständig. Dies soll nur ein
kleiner Auszug darstellen.
Literatur:
- Bernhard – Kopp, Repetitorium Mathematik, Verlag Hölder- Pichler- Tempsky
- Götz, Reichel, Müller, Hanisch, Lehrbuch der Mathematik 7, öbv&hpt
- Harald
Scheid,
Wahrscheinlichkeitsrechnung,
Mathematische
Texte
Band
6,
Wissenschaftsverlag Mannheim, Leipzig, Wien, Zürich
- Ivo Schneider, aus Geschichte der Algebra, Kapitel 8 Algebra in der frühen Glücksspiel- und
Wahrscheinlichkeitsrechnung
- Stöcker, Taschenbuch Mathematischer Formeln und moderner Verfahren, Verlag Harri
Deutsch, Thun und Frankfurt am Main
16