Wahrscheinlichkeitsrechnung

Wahrscheinlichkeitsrechnung
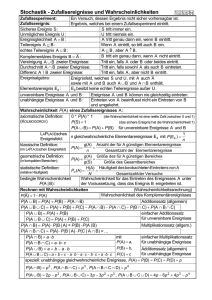
Wichtige Begriffe
Zuerst einmal müssen wir uns mit einigen Begriffen der Wahrscheinlichkeitsrechnung
auseinandersetzen:
Zufallesexperiment: Der Ausgang eines Versuches ist nur vom Zufall abhängig
Elementarereignis: Damit bezeichnet man jedes erdenkliche Ergebnis eines
Zufallsexperiments
Ereignisraum: hier fassen wir alle Elementarereignisse zusammen. Nennt man auch
Menge der Elementarereignisse.
Ereignis : jetzt wird die mathematische Definition kompliziert, man definiert ein
Ereignis als Teilmenge des Ereignisraumes.
Ereignis
Elementarereignis
Ereignisraum oder Menge der
Elementarereignisse
Wahrscheinlichkeit 2
Sind alle Ergebnisse eines Zufallsexperiments gleichwahrscheinlich, dann kann man die Wahrscheinlichkeit p(A),
wobei A ein mögliches Ereignis ist, nach LaPlace folgendermaßen berechnen:
p( A) 
Anzahl der günstigen Fälle
Anzahl der möglichen Fälle
aber das habt ihr ja schon gehört..
Nehmen wir wieder das Beispiel des Würfelns her:
Das Zufallsexperiment = das Werfen der Würfel
Elementarereignis = die geworfenen Augenzahl (1, 2, 3, 4, 5, oder 6)
Ereignisraum = {1; 2; 3; 4; 5; 6}
Ereignis= da gibt es viele Möglichkeiten; einige Beispiele: Eine gerade Zahl werfen; eine Zahl größer als 4
werfen; genau die Zahl 5 werfen,usw.
Sei das Ereignis A der Wurf einer geraden Zahl, so ist p(A)=3/6
also p(A) =1/2=0,5
Das heißt die Wahrscheinlichkeit eine gerade Zahl zu werfen liegt bei 50%.
Wie kann man dieses Ergebnis interpretieren?
Wahrscheinlichkeit 3
Wenn wir das Zufallsexperiment viele Male wiederholen, wird die Anzahl der geraden Augenzahlen
ungefähr gleich der Anzahl der ungeraden Augenzahlen sein.
Dies bedeutet, dass die berechnete Wahrscheinlichkeit ungefähr gleich der relativen Häufigkeit sein wird.
Hier kommen wir zum Gesetz der großen Zahlen:
Je größer die Anzahl von Versuchen ist, desto deutlicher stabilisiert sich die relative Häufigkeit eines
Ereignisses um einen bestimmten festen Wert – seine Wahrscheinlichkeit.
Die Wahrscheinlichkeit kann als Zahlenwert (Gott sei Dank, sonst könnten wir ja nicht damit rechnen)
zwischen 0 und 1 ausgedrückt werden
0
1
0%
100%
unmögliches Ereignis
sicheres Ereignis
In unserem Beispiel wäre der Wurf der Zahl 7 ein unmögliches Ereignis, der Wurf
einer Zahl zwischen 1 und 6 ein sicheres Ereignis.
Wahrscheinlichkeit 4