ZiB / Rechnen Bruchrechnen Gerader Ungerader Gemischt

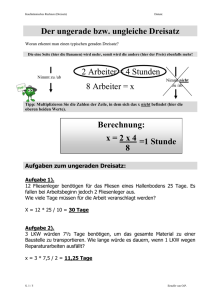
ZiB / Rechnen
ZIB / RECHNEN
Bruchrechnen
Modul 3: Dreisatz
 Gerader
 Ungerader
 Gemischt
 Kettensatz
S. 1 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Der gerade bzw. gleiche Dreisatz
Woran erkennt man einen typischen geraden Dreisatz?
Die eine Seite (hier die Bananen) wird mehr, somit wird die andere (hier der Preis) ebenfalls
mehr!
Nimmt zu /ab
2 Bananen = 0,60 €
12 Bananen = x
Nimmt auch
zu /ab
Tipp: Multiplizieren Sie die Zahlen, die neben und über dem „ x “ stehen und teilen es
durch die dritte Zahl (hier die 2)!
Berechnung:
x = 0,6 x 12 =3,60 €
2
Aufgaben zum geraden Dreisatz:
Aufgabe 1).
Wie viel Flaschen Rotwein erhält Frau B. für 161,00 €, wenn sie 12
Flaschen Rotwein zu 84,00 € gekauft hat.
x = 161 * 12 / 84 =23 Flaschen
Aufgabe 2).
1000 g Lachs kosten 18,20 Euro. Frau Bauer kauft 318 Gramm; wie viel
bezahlt sie?
x = 318 * 18,2 / 1000 = 5,79 €
Aufgage 3).
Ein Pkw verbraucht auf einer Strecke von 175 km 10,5 Liter
Dieselkraftstoff.
Welchem Verbrauch je 100 km entspricht das?
S. 2 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
x = 100 * 10,5 / 175 = 6 Liter
Aufgabe 4).
3,25 m Kabel kosten 29,50 Euro.
Wie viel kosten 2,8 m des gleichen Kabels?
x = 2,8 * 29,5 / 3,25 = 25,42 €
Aufgabe 5).
Ein Gardinenstoff kostet bei 150 cm Breite 16,95 Euro je Meter. Wie viel
kostet ein Stoff gleicher Qualität je Meter, wenn er 1,6 m breit ist.
x = 1,6 * 16,95 / 1,5 = 18,08 €
Aufgabe 6).
Für die Herstellung von 100 Teilen werden 7,25 t Blech benötigt. Wie viel
Blech muss für 120 Teile bereitgestellt werden?
x = 120 * 7,25 / 100 = 8,7 t Blech
Aufgabe 7).
Wie viel kosten 375 g, wenn ein Pfund 7,50 Euro kostet?
x = 375 * 7,5 / 500 = 5,63 €
Aufgabe 8).
7,5 m eines Kostümstoffes kosten 255,75 Euro. Es werden 3 Kostüme
aus diesem Stoff angefertigt, für die 2,5 m, 2,25 m und 2,2 m benötigt
werden. Wie viel Euro kostet der gesamte Stoff.´
2,5 + 2,25 + 2,2 = 6,95 m ; x = 6,95 * 255,75 / 7,5 = 237 €
Aufgabe 9).
Das Betonieren einer Grube, die 8 m lang, 3,5 m breit und 2 m tief ist,
kostet 8.400,00 Euro. Wie viel kostet die gleiche Arbeit für eine Grube
von 4,5 m x 2 m x 3,5 m Ausmaß?
8 * 3,5 * 2 = 56 cbm,
S. 3 / 19
x = 31,5 * 8400 / 56 = 4.725,00 €
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
4,5 * 2 * 3,5 = 31,5 cbm
Aufgabe 10).
Ein Hotel mit 90 Betten ist zu 2/3 belegt und verkauft dabei je Woche 75
Flaschen Wein. Die Hauptsaison von 14 Wochen ist ausgebucht.
Wie viele Flaschen Wein müssen für die Saison eingekauft werden?
x = 75 = 2/3; x = 100; x = 75 * 3 / 2 = 112,5 (1 Wo. Ausgebucht) * 14
= 1.575 Fl. Wein
Aufgabe 11).
Frau P. erreichte bei einem Rechentest von 20 möglichen Punkten 16,5
Punkte. Wie viele Punkte muss er in einem Test mit 60 möglichen
Punkten erreichen, wenn sie ein gleich gutes Resultat erzielen will?
x = 16,5 * 20 / 60 = 49,5 Punkte
Aufgabe 12).
Eine maschinelle Anlage sortiert in 45 Stunden 45.000 Flaschen. Wie viel
Flaschen weniger wir die Anlage in 23,5 Stunden sortieren?
x = 23,5 * 45000 / 45 = 23500; 45000 – 23500 = 21.500 Flaschen
weniger.
Aufgabe 13).
Herr Buchbach verdiente im letzten Monat ein festes Gehalt von
1.500,00 Euro und eine vom Umsatz abhängige Provision von 1.230,00
Euro. Der Monatsumsatz seiner Filiale betrug 240.000,00 Euro.
Wie viel verdient er in diesem Monat bei einem Monatsumsatz von
320.000,00 Euro?
X = 320000 / 240000 * 1230 = 1640 + 1500 = 3.140,00 €
Aufgabe 14).
Frau Wendler tapezierte eine Wand von 8 m Länge und 5 m Breite und
benötigte dafür 90 m Tapeten. Wie viel braucht sie für eine Wand von 8
Quadratmetern?
8 * 5 = 40 qm;
S. 4 / 19
x = 8 * 90 / 40 = 18 m Tapete
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Aufgabe 15).
Herr Motzke fuhr auf seiner Fahrt von Berlin nach Süddeutschland am
ersten Tag bei einer Durchschnittsgeschwindigkeit von 45 km/h 360 km.
Wie viel km mehr fuhr er am zweiten Tag, wenn er seine
Durchschnittsgeschwindigkeit um 15 km/h erhöhen konnte und die
tägliche Fahrzeit unverändert blieb?
x = 15 * 360 / 45 = 120 km mehr
Alternativ: 60 * 360 / 45 = 480 – 360 = 120 km mehr
Aufgabe 16).
100 kg eines Hilfsstoffes kosten 432,50 €. Was kosten 86,5 kg?
x = 86,5 * 432,5 / 100 = 374,11 €
Aufgabe 17).
Ein Lebensmittelgeschäft bietet eine 0,7-l-Flasche Weißwein zu 3,99 €
an. Wie viel kostet ein Liter?
x = 3,99 / 0,7 = 5,70 €
Aufgabe 18).
Eine Gesellin verdient pro Stunde 14,20 € brutto. Wie hoch ist der
Brutto-Wochenlohn, wenn 42 Stunden und 12 Minuten gearbeitet
wurden?
x = 2532 * 14,2 / 60 = 599,24 € (alternativ: 42,2 * 14,2 = 599,24 €)
Aufgabe 19).
Die Elektrizitätskosten für ein Firmengebäude von 254 qm Nutzfläche
betrugen 1.346,20 €. Wie hoch waren jeweils die Kosten für den
2. Stock (70 qm) und für den 4. Stock (84 qm)?
 2. Stock: x = 70 * 1346,2 / 254 = 371,00 €
 4. Stock: x = 84 * 1346,2 / 254 = 445,20 €
Aufgabe 20).
Herr Schlaufuchs benötigte für 15 Aufgaben 5 Minuten und 20
Sekunden. Wie viel Aufgaben schafft er in 90 Minuten und 40 Sekunden?
x = 5440 * 15 / 320 = 255 Aufgaben
S. 5 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Der ungerade bzw. ungleiche Dreisatz
Woran erkennt man einen typischen geraden Dreisatz?
Die eine Seite (hier die Bananen) wird mehr, somit wird die andere (hier der Preis) ebenfalls
mehr!
Nimmt zu /ab
2 Arbeiter = 4 Stunden
8 Arbeiter = x
Nimmt nicht
zu /ab
Tipp: Multiplizieren Sie die Zahlen der Zeile, in dem sich das x nicht befindet (hier die
oberen beiden Werte).
Berechnung:
x = 2 x 4 =1 Stunde
8
Aufgaben zum ungeraden Dreisatz:
Aufgabe 1).
12 Fliesenleger benötigen für das Fliesen eines Hallenbodens 25 Tage.
Es fallen bei Arbeitsbeginn jedoch 2 Fliesenleger aus.
Wie viele Tage müssen für die Arbeit veranschlagt werden?
X = 12 * 25 / 10 = 30 Tage
Aufgabe 2).
3 LKW würden 7½ Tage benötigen, um das gesamte Material zu einer
Baustelle zu transportieren. Wie lange würde es dauern, wenn 1 LKW
wegen Reparaturarbeiten ausfällt?
x = 3 * 7,5 / 2 = 11,25 Tage
S. 6 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Aufgage 3).
6 Pumpen benötigen zum Beladen eines Tankschiffs 16 Stunden. In
welcher Zeit hätte das Tankschiff beladen werden können, wenn 2
Pumpen mehr zur Verfügung gestanden hätten?
x = 6 * 16 / 8 = 12 Stunden
Aufgabe 4).
6 Pumpen benötigen zum Beladen eines Tankschiffs 8 Stunden.
Wie viele Pumpen hätten abgeschaltet werden können, wenn zur
Belandung 4 Stunden mehr Zeit gewesen wäre?
x = 6 * 8 / 12 = 4; 6 – 4 = 2 Pumpen hätten abgeschaltet werden
können.
Aufgabe 5).
Eine Planierraupe ebnet ein Grundstück von 30 m Länge und 14 m Breite
in 4 Tagen. Ein großes Grundstück von 630 qm soll im Auftrag der
Gemeinde in 6 Tagen geebnet werden. Kann der Auftrag erfüllt werden?
30 * 14 = 420 qm * 6 / 630 = 4; Ja, kann erfüllt werden.
Aufgabe 6).
Ein Käufer tauscht 12 Gläser zu je 30,00 € gegen solche zu je 18,00 €
um. Wie viel Stück erhält er für den gleichen Betrag?
x = 12 * 30 / 18 = 20 Gläser
Aufgabe 7).
Frau Meier tauscht 18 Bestecke zu je 14,00 € gegen andere zu je 15,75
€ um.
Wie viele Bestecke erhält sie, wenn der Rechnungsbetrag gleich bleiben
soll?
S. 7 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
x = 18 * 14 / 15,75 = 16 Bestecke
Aufgabe 8).
27 Betonfacharbeiter brauchen für einen Rohbau 56 Tage.
Wie lange würden 24 Arbeiter benötigen?
x = 27 * 56 / 24 = 63 Tage
Aufgabe 9).
In ein Regal passen 40 Ordner von 50 mm Breite. Es sollen neue Ordner
mit einer Breite von 80 mm eingeführt werden. Wie viele Ordner würden
in das alte Regal passen ?
X = 40 * 50 / 80 = 25 Ordner
Aufgabe 10).
Fünf Verkäufer brauchen für eine Inventur 18 Stunden. Wie viele
Stunden würden 6 Verkäufer brauchen?
x = 5 * 18 / 6 = 15 Stunden
Aufgabe 11).
Eine sechsköpfige Feriengruppe würde in Frankreich 22 Tage bleiben
können, wenn sie 180,00 € pro Tag ausgeben würde. Um wie viel Tage
müsste die Gruppe den Urlaub verkürzen, wenn ihre täglichen Ausgaben
auf 220,00 € steigen würden?
x = 22 * 180 / 220 = 18; 22 – 18 = 4 Tage weniger
Aufgabe 12).
Eine Hamburger Firma produziert ihre Geräte in einer Fabrikhalle, die 75
m lang und 22 m breit ist. Die Firma will ihren Standort nach Lübeck
verlegen, wo ihr eine gleich große Halle angeboten wird, die 55 m lang
ist. Wie breit ist die neue Fabrikhalle?
S. 8 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
75 * 22 = 1650 qm; 1650 / 55 = 30 m breit
Aufgabe 13).
Familie F. hat in den Ferien eine Radtour von 7 Tagen gemacht und ist
mit einer Durchschnittsgeschwindigkeit von 12 km/h gefahren.
Wie schnell müsste die Familie fahren, wenn sie die gleiche Strecke in 6
Tagen schaffen will?
x = 7 * 12 / 6 = 14 km/h
Aufgabe 14).
Eine Gemeinde von 18.000 Einwohnern verbrauchte insgesamt
3.420.000 Liter Wasser. Wie viel Einwohner hatte die Gemeinde, die
insgesamt gleichviel, aber pro Kopf 30 Liter Wasser weniger
verbrauchte?
3420000 / 18000 = 190 l je Einwohner:
x = 18000 * 190 / 160 = 21.375 Einwohner
Aufgabe 15).
3 Wirtschafterinnen benötigen zur Reinigung einer Großküche 460
Minuten. Wie viele Stunden brauchen 2 Wirtschafterinnen für die gleiche
Arbeit?
x = 3 * 460 / 2 = 690 Minuten = 11 Std. 30 Minuten
Aufgabe 16).
Mit einer Durchschnittsgeschwindigkeit von 80 km/h erreicht ein
Autofahrer sein Ziel in 6 Stunden.
Wie schnell müsste er durchschnittlich fahren, wenn er schon in 5
Stunden 30 Minuten am Bestimmungsort sein will?
x = 80 * 6 / 5,5 = 87,27 km/h
Aufgabe 17).
Peter rechnet sich aus, dass er für einen Urlaub von 14 Tagen jeden Tag
42,00 € Taschengeld zur Verfügung hat. Wie viel Euro kann er täglich
ausgeben, wenn er 3 Wochen Urlaub macht?
x = 14 * 42 / 21 = 28,00 €
S. 9 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Aufgabe 18).
Wie viele Stunden und Minuten benötigt ein Radprofi für eine Strecke
von 348 km, wenn seine durchschnittliche Geschwindigkeit 40 km in der
Stunde ist?
x = 348 * 60 / 40 = 8,7 Std. (8 Std. 42 Minuten, da 0,1 = 6 Minuten)
Aufgabe 19).
Heinz kaufte 12 Teller zum Preis von 2,50 € pro Stück. Wie viel Teller
erhält er beim Umtausch, wenn nur noch Teller zum Preis von 1,00 €
vorrätig sind?
x = 12* 2,5 / 1 = 30 Teller
Aufgabe 20).
Ein Autofahrer benötigt für eine Strecke von 170 km 3 Std. und 20
Minuten.
Wie lange braucht er bei gleicher Geschwindigkeit für eine 30 km längere
Strecke?
x = 200 x 200 / 170 = ca. 235 Minuten (3 Stunden, 55 Minuten)
S. 10 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Wiederholungsübungen zum einfachen Dreisatz (gerader, ungerader)
Aufgabe 1).
3 Produktionsautomaten erledigen einen Auftrag in 15 Stunden. Wie
lange würden 5 Automaten mit gleicher Leistung benötigen?
Ungerader Dreisatz:
3 Produktionsautomaten
5
=
=
15 Stunden
x
x=3*15/5=9 Stunden
Aufgabe 2).
Zur Durchführung einer Kanalisation benötigt ein Unternehmer bei 5
Arbeitstagen 18 Arbeiter. Die Arbeit soll in 3 Tagen beendet sein. Wie
viel Arbeiter muss er noch zusätzlich einstellen?
Ungerader Dreisatz:
5 Arbeitstage
3
=
=
18 Arbeiter
x
x = 5x*18/3=30 Arbeiter–18 Arbeiter=12 zusätzliche Arbeiter
Aufgabe 3).
9 Angestellte erledigen die Inventur eines Warenlagers in 8 Tagen zu
je 8 Arbeitsstunden. In welcher Zeit kann die Inventur fertig sein,
wenn noch 3 Hilfskräfte hinzugezogen werden?
Ungerader Dreisatz:
9 Angestellte
12
=
=
8 Tage
x
x = 9*8/12=6 Tage
Aufgabe 4).
Um einen Fußboden, der 4,5 m lang und 4,2 m breit ist, mit
Fußbodenlack zu streichen, braucht man 2,1 kg Lack. Wie viel kg
braucht man im Ganzen, wenn noch 2 weitere Böden von 4,75 m
Länge und 4,4 m Breite bzw. 6,8 m Länge und 1,4 m Breite gestrichen
werden sollen?
Gerader Dreisatz:
18,9 qm
49,32 qm
=
=
2,1 kg Lack
x
NR:20,9+9,52+18,9=49,32qm
x = 49,32*2,1/1 8,9=5,48 kg
S. 11 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Aufgabe 5).
46,5 m Tuch kosten 1.720,75 €
Wie viel kosten 3,75 m dieses Tuches?
Gerader Dreisatz:
46,5 m = 1720,75 €
3,75 m = x
x=3,75*1720,75/46,5=138,77 €
Aufgabe 6).
Das Ausheben einer Grube, die 8 m lang, 3,5 m breit und 2 m tief ist,
verursacht 1.252,00 € Kosten, bemessen nach dem Rauminhalt. Wie
hoch sind die Kosten für das Ausheben einer Grube im Ausmaß von
4,5 x 2 x 3 m?
Gerader Dreisatz:
56 cbm
27 cbm
= 1252,00 €
=x
x = 27*56/1252=603,64 €
Aufgabe 7).
Ein Autoverleih berechnet für einen PKW für 12 Tage 1.140,00 €. Die
Leihe wird um 9 Tage verlängert. Wie viel € muss für die gesamte
Leihdauer bezahlt werden?
Gerader Dreisatz:
12 Tage = 1140,00 €
21 Tage = x
x=21*1140/12=1995 €
Aufgabe 8).
Wie viel Liter Heizöl erhält man für 907,50 € wenn 700 Liter 385,00 €
kosten?
Gerader Dreisatz:
700 Liter
x
=
=
385,00 €
907,50 €
x=700*907,50/385=1650 €
S. 12 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Aufgabe 9).
Ein Lebensmittelvorrat reicht für 16 Personen 42 Tage. Wie viele
Tage könnten 12 Personen bei gleichem Verzehr pro Kopf davon
essen?
Ungerader Dreisatz:
16 Personen =
12 Personen =
42 Tage
x
x = 16*42/12=56 Tage
Aufgabe 10).
Für Montagearbeiten an 9 Tagen erhalten 3 Arbeitskräfte zusammen
4.320,00 €. Wie viel müsste der Betrieb zahlen, wenn 7 Arbeitskräfte
6 Tage beschäftigt werden würden?
Gerader Dreisatz.
27 Tage/Arbeitskräfte
42
=
=
4320 €
x
x=42*4320/27=6720 €
Aufgabe 11).
Wie viele Stunden braucht ein Radfahrer, um eine 90 km lange
Strecke zurückzulegen, wenn seine durchschnittliche Geschwindigkeit
15 km/h beträgt?
Gerader Dreisatz
15 km =
90 km
1 Std.
x
x=90*1/15=6 Std.
Aufgabe 12).
Ein Arbeiter stellt eine Tasche in 55 Minuten her. Wie viele
Erzeugnisse könnte er theoretisch in 8 Stunden fertigen? (auf 2
Nachkommstellen runden)
Gerader Dreisatz
1 Tasche
x
=
=
55 Minuten
480 Minuten
x=480*1/55=8,7272727 = 8,73 Taschen
Aufgabe 13).
S. 13 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Für den Umsatz von 448,00 € erhält eine Verkäuferin eine Prämie von
11,20 €. Wie hoch ist die Prämie ihrer Kollegin, die 250,00 € Umsatz
erzielt hat?
Gerader Dreisatz
448,00 €
250,00 €
=
=
11,20 €
x
x=250*11,20/448=6,25 €
Aufgabe 14).
Einem Reisenden werden für eine Geschäftsreise von 26 Tagen
täglich 24 € Spesen erstattet. Früher erhielt er nur 20,00 €. Wie viel
volle Tage käme er heute mit dem früheren Satz aus?
Gerader Dreisatz:
26 Tage
x
=
=
24 €
20 €
x=20*26/24=21,67 €
Aufgabe 15).
Die Fortbildungskosten eines EDV-Seminars für 8 Mitarbeiter
belaufen sich auf 90.000,00 €.
Auf welchen Betrag steigen die Kosten, wenn im nächsten Jahr 4
Personen mehr ausgebildet werden.
Gerader Dreisatz:
8 Mitarbeiter
12 Mitarbeiter
=
=
90000 €
x
x = 12*90000/8=135000 €
Aufgabe 16).
4,50 m Teppichboden von 3 m Breite kosten 810,00 €. Wie viel
kosten 3 m Bodenbelag in einer Breite von 2 m?
Gerader Dreisatz:
13,5 qm
6 qm
=
=
810,00 €
x
x=6*810/13,5=360 €
Aufgabe 17).
Ein Lebensmittelgeschäft bietet eine 0,7-l-Flasche Rotwein zu 3,99 €
an. Wie viel kostet ein Liter?
Gerader Dreisatz
0,7 l
1l
=
=
3,99 €
x
x = 1*3,99/0,7=5,70 €
S. 14 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Aufgabe 18).
100 kg eines Hilfsstoffes kosten 432,50 €.
Was kosten 86,5 kg?
Gerader Dreisatz
100 kg
86,5 kg
=
=
432,50 €
x
x = 86,5*432,5/100=374,11 €
Aufgabe 19).
14 Vollautomaten haben eine Kapazität von 21.000 Stück. Sie soll auf
30.000 Stück erhöht werden. Wie viele Automaten sind zusätzlich
anzuschaffen?
Gerader Dreisatz
14 Vollautomaten
x
=
=
21000 Stück
30000 Stück
x=14*30000/21000=20-14= 6 zusätzliche Automaten
Aufgabe 20).
Ein Käufer tauscht 12 Gläser zu je 30,00 € gegen solche zu je 18,00 €
um. Wie viel Stück erhält er für den gleichen Betrag?
Ungerader Dreisatz
12 Gläser
x
=
=
30 €
18 €
x=12*30/18=20 Gläser
S. 15 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Wiederholungsübungen zum Kettensatz - Lösungsansätze
Aufgabe 1).
In 4 Monaten wurden von 250 Beschäftigten 2700 kg Farbe
verbraucht. Wie viel Farbe brauchen 225 Arbeiter in 3 Monaten?
x = 2700 kg * ¾ * 225 / 250 = 1.822,5 kg
Aufgabe 2).
10 Monteure verlegen in 5 Arbeitstagen zu je 8 Stunden 6000 m
Kabel. Da sich zwei Monteure krankgemeldet haben, müssen die
anderen eine Überstunde pro Tag machen.
Wie viel Meter Kabel verlegen sie in 12 Arbeitstagen?
x = 6000 * 8/10 * 9/8 * 12/5 = 12.960 m
Aufgabe 3).
Mit 20 Maschinen können in 5 Tagen zu je 8 Arbeitsstunden 10500
Werkstücke hergestellt werden.
Wie viele Werkstücke können in 6 Tagen zu je 7 Arbeitsstunden mit
nur 12 Maschinen hergestellt werden?
x = 10500 * 6/5 * 7/8 * 12/20 = 6.615 Stück
Aufgabe 4).
In einer Fabrik erzeugen 7 Maschinen in 14 Arbeitstagen 19.600
Ersatzteile, wenn 8 Stunden täglich gearbeitet wird. Aufgrund eines
Konjunkturabschwungs muss Kurzarbeit eingeführt werden, sodass
nur noch 5 Maschinen täglich 5 Stunden laufen.
Wie viele Teile werden jetzt in 22 Werktagen produziert?
= 19600 * 5/7 * 22/14 * 5/8 = 13.750 Teile
Aufgabe 5).
Ein Werbefilm von 15 Sekunden Dauer läuft an 15 Tagen im Monat
im Werbefernsehen eines Privatsenders. Die Übertragungskosten
hierfür beliefen sich auf 555.000 €.
Um wie viel müsste der Werbeetat erhöht werden, wenn in Zukunft an
25 Tagen zweimal je 15 Sekunden geworben werden soll.
x = 555000 * 30/15 * 25/15 =
1.850.000 € - 555.000 € = 1.295.000 €
S. 16 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Aufgabe 6).
Eine Sportschule kauft für eine Mannschaft von 12 Personen, die 5
Tage bleiben wollen, 15 kg Gemüse. Da die Delegation jedoch aus 14
Personen besteht, die zudem einen längeren Aufenthalt in Aussicht
gestellt haben, werden noch mal 13 kg gekauft.
Wie lange reicht das Gemüse bei gleichem Speiseplan?
x = 5 * 12/14 * 28/15 = 8 Tage
Aufgabe 7).
Erfahrungsgemäß benötigen 3 Küchenhilfen zur Zubereitung von 120
Essensportionen in einem Kinderheim täglich 4 Stunden. Wie viele
Küchenhilfen müssten zusätzlich eingestellt werden, wenn 150
Portionen angerichtet werden sollen und die Arbeitszeit um 1 Stunde
täglich reduziert werden soll?
x = 3 * 150/120 * 4/3 = 5 – 3 = 2 Küchenhilfen zusätzlich
Aufgabe 8).
Einen Auftrag über 55 Werkstücke erledigen 15 Arbeiter in 12 Tagen
bei einer täglichen Arbeitszeit von 8 Stunden. Ein Eilauftrag über 77
Stücke soll in 9 Tagen ausgeführt werden.
Wie viele Arbeiter müssten zusätzlich eingestellt werden, wenn
Überstunden vermieden werden?
x = 15 * 77/55 * 12/9 = 28 – 15 = 13 zusätzliche Arbeiter
Aufgabe 9).
Eine Kleiderfabrik produziert täglich 128 Kostüme, wenn 28
Fachkräfte täglich 8 Stunden arbeiten. Aufgrund betrieblicher
Vereinbarungen wird die tägliche Arbeitszeit auf 7 Stunden
herabgesetzt.
Wie hoch ist die tägliche Produktion, wenn 9 zusätzliche Fachkräfte
eingestellt werden?
x = 128 * 37/28 * 7/8 = 148 Stück
Aufgabe 10).
Zur Herstellung einer Werkzeugmaschine benötigen 28 Arbeiter bei
einer täglichen Arbeitszeit von 8 Stunden 12 Tage. Wenn nur 8 Tage
zur Verfügung stehen und nur 7 Stunden täglich gearbeitet werden
soll, wie viele Arbeiter müssten zusätzlich eingestellt werden?
x = 28 * 8/7 * 12/8 = 48 – 28 = 20 zusätzliche Arbeiter.
S. 17 / 19
Erstellt von O.P.
ZiB / Rechnen
Bruchrechnen
Notizen
S. 18 / 19
Erstellt von O.P.
ZiB / Rechnen
S. 19 / 19
Bruchrechnen
Erstellt von O.P.