KLL-112 - Mathematik

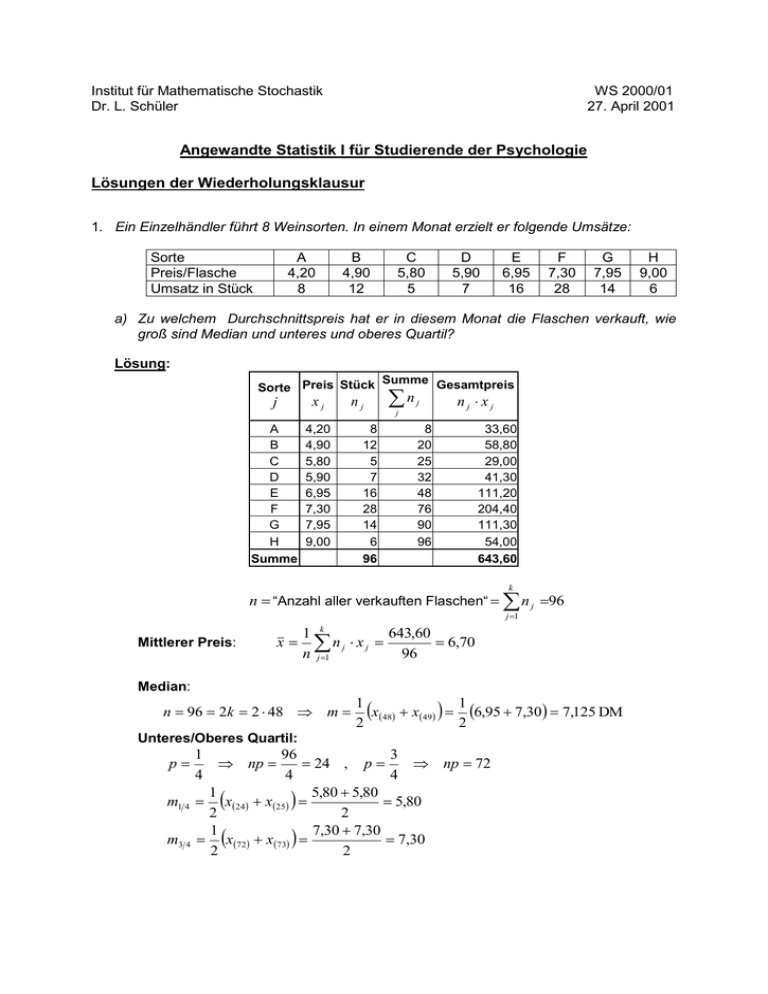
Institut für Mathematische Stochastik
Dr. L. Schüler
WS 2000/01
27. April 2001
Angewandte Statistik I für Studierende der Psychologie
Lösungen der Wiederholungsklausur
1. Ein Einzelhändler führt 8 Weinsorten. In einem Monat erzielt er folgende Umsätze:
Sorte
Preis/Flasche
Umsatz in Stück
A
4,20
8
B
4,90
12
C
5,80
5
D
5,90
7
E
6,95
16
F
7,30
28
G
7,95
14
H
9,00
6
a) Zu welchem Durchschnittspreis hat er in diesem Monat die Flaschen verkauft, wie
groß sind Median und unteres und oberes Quartil?
Lösung:
Summe Gesamtpreis
Sorte Preis Stück
j
A
B
C
D
E
F
G
H
Summe
xj
4,20
4,90
5,80
5,90
6,95
7,30
7,95
9,00
nj
8
12
5
7
16
28
14
6
96
n
j
j
nj  xj
8
20
25
32
48
76
90
96
33,60
58,80
29,00
41,30
111,20
204,40
111,30
54,00
643,60
k
n  “Anzahl aller verkauften Flaschen“   n j 96
j 1
Mittlerer Preis:
x
k
1
643,60
nj  xj 
 6,70

n j 1
96
Median:
n  96  2k  2  48  m 
1
x48  x49   1 6,95  7,30  7,125 DM
2
2
Unteres/Oberes Quartil:
1
96
3
 np 
 24 , p 
 np  72
4
4
4
1
5,80  5,80
m1 4  x24  x25  
 5,80
2
2
1
7,30  7,30
m3 4  x72  x73  
 7,30
2
2
p
b) Der Händler vermutet, dass die Kunden ihr Kaufverhalten nicht ändern, wenn er jede
Flasche 0,50 DM teurer verkauft. Wie ändern sich der mittlere Verkaufspreis und die
Streuung des Preises.
Lösung:
Neue Preise: y j  x j  0,50  j  1, , k  
Neuer mittlerer Verkaufspreis:
Neue Streuung:
y  x  0,50 ,  y   x
y  6,70  0,50  7,20 DM
identisch mit alter Streuung
2. In einer Studie soll der Zusammenhang zwischen Übergewicht und Bluthochdruck
untersucht werden. In der folgenden Tabelle wurde der BodyMassIndex X (BMI =
Gewicht in kg / (Körpergröße in m)²) und der systolische Blutdruck Y an 6 Männern
erhoben.
xi
26
23
27
28
24
25
yi
170
150
160
175
155
150
Ermitteln Sie den empirischen Korrelationskoeffizienten und interpretieren diesen Wert.
Stellen Sie die lineare Gleichung für die Regressionsgerade y  a  x  b auf ( a und b
berechnen!).
Geben Sie Schätzungen an für den systolischen Blutdruck eines Mannes, der 174 cm
groß und 84 kg schwer ist, und einer Frau, die 1,68 m groß und 56 kg schwer ist, falls es

Gewicht in kg 
.
Größe in m2 
aus den Daten sinnvoll ist  BMI 

Lösung:
i
xi
1
2
3
4
5
6
26
23
27
28
24
25
153
yi
x i2
x yj
y i2
170 676 28900
150 529 22500
160 729 25600
175 784 30625
155 576 24025
150 625 22500
960 3919 154150
4420
3450
4320
4900
3720
3750
24560
153
960
 25,5 , y 
 160,0 ,
6
6
1
1
s x2  3919  6  25,5 2  3,5 , s y2  154150  160,0 2  110,0
5
5
1
s xy  24560  6  25,5  160,0  16,0
5
s xy
16,0
rxy 

 0,81544
3,5  110,0
s x2  s y2
x




Es liegt eine starke positive Korrelation vor, mit wachsenden BMI-Werte wachsen
auch die systolischen Blutdruckwerte.
aˆ 
s xy
s
2
x

16,0
 4,57 , bˆ  y  aˆ  x  160,0  4,57  25,5  43,43
3,5
Schätzung für eine Frau aus diesen Werten nicht zulässig, da nur Daten von Männern
vorliegen.
Schätzung für den Mann: BMI 
84
 27,645 (Wert liegt im Bereich der Daten)
1,74 2

y  a  x  bˆ  4,57  27,645  43,43  170,3
3. In einer deutschen Mittelstadt sollte untersucht werden, wie weit die
Religionszugehörigkeit Einfluss auf den schulischen Erfolg hat. Dazu wurde ausgezählt,
wie viele aller Frauen und Männer im Alter von 25 Jahren bestimmten
Religionsgemeinschaften angehören und welchen höchsten Schulabschluss sie besitzen.
Dabei
wird
hier
nur
zwischen
evangelisch/katholisch/sonstige
bzw.
Abitur/Realschulabschluss/Übrige unterschieden. Sowohl bei den evangelischen als auch
bei den katholischen 25jährigen haben 50% das Abitur und 30% den Realschulabschluss.
Unter allen 25jährigen haben 40% Abitur und ebenfalls 30% den Realschulabschluss.
Unter den 25jährigen sind gleich viele evangelisch wie katholisch. 40% gehören den
übrigen Religionsgemeinschaften an.
 Fertigen Sie eine Kontingenztafel der Wahrscheinlichkeiten an, in dieser Stadt zufällig
einen 25jährigen Bewohner mit den obigen Eigenschaften auszuwählen, und
ermitteln Sie die fehlenden Daten.
 Sind bei der zufälligen Auswahl unter den 25jährigen Bewohnern der Stadt die
Ereignisse A  “ein Gymnasiast wird ausgewählt“, bzw. B  “ein Bürger einer der
übrigen Religionsgemeinschaften wird gewählt“, unabhängig (Nachweis durch
Ausrechnen!“).
Lösung:
S\R
Gym
RS
übrige
ev
0,15
0,09
0,06
rk sonstige SUMME
0,40
0,15
0,10
0,30
0,09
0,12
0,30
0,06
0,18
SUMME
0,30
0,30
0,40
1,00
Pev   P(rk ) 
1
1  P(sonst )  1 1  0,4  0,3
2
2
PGymnasium umd evangelisc h   PGym | ev P(ev)  0,5  0,3  0,15  PGymnasium umd katholisch
PRS und ev   PRS | ev P(ev)  0,3  0,3  0,09
PGym  0,4 , P( RS )  0,3
Restliche Werte der Tafel durch Summenbildung.
P(A) =
P(B) =
P(A) P(B) =
P(AB) =
0,40
0,40
0,16
0,10
Also sind A und B nicht unabhängig!

4. Ein Glückspiel wird mit zwei Würfeln durchgeführt Ein Spieler erhält als Gewinn
 9 DM, wenn beide Würfel eine 1 oder beide eine 6 zeigen,
 1 DM, wenn mindestens ein Würfel eine 1 oder 6 zeigt, aber nicht beide eine 1 oder
beide eine 6,
 0 DM in allen anderen Fällen.
Wie hoch muss der Einsatz für ein Spiel mindestens sein, damit im Mittel nicht mehr als
50% des Einsatzes ausgeschüttet werden müssen?
Lösung:
 1,1 

 
6,1 

X 
1,6

  ,
6,6
  36
“Auszahlung in DM“
P X  9  P1,1, 6,6 
2
1

 0,0555
36 18
P X  1  P1,2,, 1,6, 6,1,, 6,5, 2,1,, 5,1, 2,6 5,6 
18 1
  0,5
36 2
1 1 8 4
 
  0,4444
18 2 18 9
1
1
4 18
EX   9   1   0  
1
18
2
9 18
P( X  0)  1 
Die mittlere Auszahlung soll höchstens 50% der Einzahlung ausmachen. Damit muss die
Einzahlung mindestens das Doppelte, also 2 DM betragen.
5. Eine automatische Abfüllanlage füllt Flaschen mit Orangensaft. Die jeweils abgefüllte
Menge ist normalverteilt mit   700 ml und   12 ml .
 Wie groß ist die Wahrscheinlichkeit, dass der garantierte Mindestinhalt von 680 ml
unterschritten wird?
 Auf welchen Wert müsste  eingestellt werden, wenn ein Mindestinhalt von 680 ml
garantiert werden und die Wahrscheinlichkeit für das Einhalten dieser Grenze 0,995
betragen soll?
Lösung:


X = „Flascheninhalt“    ,  2 ,   700 ,   12
 680  700 
 5
P X  680  
      1  1,667   1  0,9522  0,0478  4,8%
12


 3
 680   
 680   
   680 
0,995  P X  680  1  
   
  

12 
 12 

 12 
  680

 2,575    12  2,575  680  710,9
12
Im Mittel sollten also 710,9 ml in jede Flasche gefüllt werden.
6. Die Wahrscheinlichkeit, dass bei einer Geburt ein Junge geboren wird, beträgt nach
allgemeiner Auffassung 50%.
a) Wie groß ist damit die Wahrscheinlichkeit, dass unter 20 Neugeborenen
 Genau 3 Jungen,
 mindestens 13 Jungen und mindestens 2 Mädchen,
 mindestens 12 Mädchen sind.
Benutzen sie eine geeignete Tabelle.
Lösung:
X = „Anzahl der Jungen“  Bi n, p  , n  20 , p  0,5
P X  3  0,0011  0,11%
P13  X  18  0,0739  0,0370  0,0148  0,0046  0,0011  0,0002  0,1316  13,16%
P X  8  0,0002  0,0011    0,739  0,1201  0,1316  0,1201  0,2517  25,17%
b) Man hat festgestellt, das in den letzten Jahren 51% aller Neugeborenen Jungen sind.
Berechnen sie jetzt die Wahrscheinlichkeit, dass unter 5 Neugeborenen genau 3
Jungen sind.
Lösung:
X = „Anzahl der Jungen“  Bi n, p , n  5 , p  0,51
 5
P X  3    0,513 0,49 2  10  0,132651  0,2401  0,3185  31,85%
 3
 5
P X  3    0,55  0,3125  31,25%
Für p  0,5 würde gelten:
 3
Hinweise:
Die Lösungen sind ab Montag, 30.4.01 am schwarzen Brett des Institutes (Forum, 6.Stock)
ausgehängt und auf der u.a. Homepage enthalten:
http://www.math.tu-bs.de/stochastik/vorl/ueb-ps1.htm .
Die Rückgabe der Klausuren und die Ausgabe der Scheine findet am Montag, 6.5.01, bei Dr.
Schüler (Forum, F 618) von 13.00 – 14.00 Uhr statt. Später sind sie im Sekretariat und bei
Dr. Schüler erhältlich. Sobald die Ergebnisse feststehen, werden sie auf der obigen InternetSeite unter Angabe der Matrikelnummer veröffentlicht. Vorherige telefonische Nachfragen
sind sinnlos.