Aufgaben zur Entscheidungstheorie

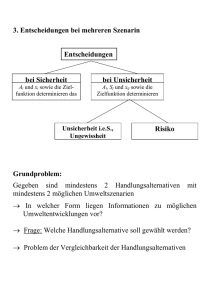
Johann Wolfgang Goethe - Universität
Frankfurt am Main
Fachbereich Wirtschaftswissenschaften
Institut für Statistik und Mathematik
Mathematik - Prof. Dr. H. Rommelfanger
Mertonstr. 17-23
Telefon (069) 798 - 23 609
14.05.2016
ENTSCHEIDUNGSTHEORIE
1. Übungsblatt
WS 03/04
1.
Erläutern Sie an den nachfolgenden Beispielen jeweils die Begriffe „Explanandum“,
„Explanans“ und die zueinander inversen Operationen „Erklärung“ und „Prognose“.
a. In den vergangenen 2 Monaten stieg die Nachfrage nach „Wäsche Weiß“ um 10%. Das
Unternehmen „Hektor & Gambit“ hat zum 1.9.98 den Preis für „Wäsche Weiß“ um 5%
gesenkt und die Werbeausgaben um 20% gesteigert.
b. Die Kosten pro Pkw konnten ab 1. September 98 um 8% gesenkt werden, nachdem in der
Betriebspause im August 98 zusätzliche Roboter in die Fertigstraßen eingebaut
(technischer Fortschritt) und gleichzeitig 10% Personal umgesetzt wurden.
2.
Worin sehen CYERT/MARCH die wesentlichen Unterschiede zwischen dem Entscheidungsverhalten eines real existierenden Unternehmens und dem Entscheidungsverhaltens eines Homo
Oeconomicus.
3.
Ein Entscheidungsträger (ET) möchte 20.000 € anlegen. Die Bank offeriert ihm die folgenden
Anlagemöglichkeiten:
I. Anlage auf einem Sparbuch zu 3% p. a., Betrag beliebig;
II. Erwerb einer Beteiligung am Unternehmen U, Beteiligungsbetrag 18.000 €;
III. Erwerb festverzinslicher Papiere des Staates S, Stückelung zu 10.000 €;
IV. Erwerb einer Beteiligung an dem Unternehmen V, Beteiligungsbetrag 10.000 €.
Wie viele und welche Aktionen gibt es für den ET nach dem Prinzip vollkommener
Alternativenstellung?
4.
Erläutern Sie die Begriffe „Höhen-“, „Arten-“, „Zeit-“ und „Unsicherheitspräferenz“ anhand
des Beispiels, dass eine Entscheidungsträgerin (ET) eine elektronisch gesteuerte
Produktionsanlage kaufen will, die ihr in den nächsten 10 Jahren Zusatzgewinne liefern und
die Mitarbeiter/innen von schweren Arbeiten entlasten soll.
5.
Gegeben sind die normalverteilten Gewinne der Aktionen a1, , a5:
N1(4; 1), N 2 (5; 12 ), N3(7; 13 ), N 4 (8; 1), N5 (8,2; 23 ).
a. Welche dieser Alternativen können mit 95,45%-Wahrscheinlichkeit als dominiert
ausgesondert werden?
b. Welche Alternative ist nach der -Regel die gewinnmaximale?
c. Die --Isolinien des ET seien gegeben durch
  12 (  1)2  C .
Zeichnen Sie einige dieser Isolinien in ein --Koordinatensystem ein. Welche der
5 Aktionen ist gemäß dieser Präferenzordnung des ET die optimale?
2
6.
Gegeben sind die Fuzzy-Zahlen
~
~
~
a. A  (8; 2; 3) LR , B  (6; 23 ; 2)LR , C  (2; 12 ; 1)RL ;
~
~
~
b. A  (12; 3; 3)LR , B  (4; 1; 1)LR , C  (3; 1; 2)RL .
~
~ ~
~
~
~ ~
~ ~
~
~ ~
B1 .
AC ,
3 A ,  2  B , A  B ,
A C ,
Bilden Sie A  B ,  B ,
Bei der erweiterten Multiplikation, Division und Inversenbildung sind jeweils beide Formeln
zu beachten.
7.
Gegeben sind die Fuzzy-Intervalle des --Typs
~
~
a. M  ( 4; 4,3; 5; 6; 6,5; 7),  und N  (10; 11; 12; 14; 16; 18),  ;
~
~
b. M  ( 2; 2,5; 3; 3; 4; 5),  und N  (10; 12; 13; 14; 15; 16),  .
~
~
~ ~
~ ~
~ ~
M  N,
Bilden Sie
N  M, M N , N M.
8.
Gegeben sind die Fuzzy-Ergebnisse der Aktionen a1, , a5
~
~
E1  (3; 3,2; 3,6; 4; 4,4; 4,7), ,
E2  (3,8; 4; 4,5; 5; 5,6; 6),  ,
~
~
E3  (7; 7,5; 8; 9; 10; 11),  ,
E4  (8; 10; 12; 14; 16; 18),  ,
~
E5  (9; 9,5; 10; 11; 12; 13),  .
a. Zeichnen Sie die Zugehörigkeitsfunktionen dieser Fuzzy-Ergebnisse in einer Koordinatenebene.
b. Welche Präferenzaussagen gelten zwischen diesen Ergebnissen bei Verwendung der -Präferenz, der -Präferenz und des Niveau-Ebenen-Verfahrens mit den drei Niveaus , , 1 ?
9.
Gegeben ist eine Entscheidungssituation mit fünf Alternativen ai, fünf möglichen Zuständen sj
und der nachstehenden Ergebnismatrix Z  ( z ij )i 1,,5 .
j1,,5
s1
s2
s3
s4
s5
a1
2
7
2
4
4
a2
5
2
4
7
3
a3
6
5
3
6
4
a4
4
1
4
6
3
a5
3
4
2
7
2
a. Eliminieren Sie alle ineffizienten Alternativen.
b. Wenden Sie
 die Maximin-Regel,
 die Maximax-Regel,
 das HURWICZ-Kriterium mit  = 0,6,
 das LAPLACE-Kriterium und
 die SAVAGE-NIEHANS-Regel
jeweils zur Auswahl einer Alternative an.
c. Berechnen Sie den Optimismusparameter * so, dass die Alternativen a1 und a3 durch das
HURWICZ-Kriterium als gleichwertig eingestuft werden.
3
d. Man gehe nun davon aus, dass eine Entscheidungssituation unter Risiko vorliegt. Folgende
Beziehungen zwischen den Eintrittswahrscheinlichkeiten der Zustände sj sind bekannt:
p1 = p4 = 0,5p5 = 0,5p3
p2 = 0,5(p3 + p5)
Ermitteln Sie hieraus die Eintrittswahrscheinlichkeiten p1, , p5. Für welche Alternative
entscheidet man sich nach dem
 -Prinzip,
 (, )-Prinzip mit (ai) = i + 0,8i ?
10.
Ein Unternehmen fertigt im Wesentlichen zwei Produkte P1 und P2. Im Laufe ihrer Fertigung
belegen die Produkte zwei Maschinen M1 (P1: 1 ZE/ME; P2: 2 ZE/ME) und M2
(P1: 1 ZE/ME; P2: 6 ZE/ME). Die beiden Maschinen stehen im relevanten Zeitraum für
1.500 ZE bzw. 2.100 ZE zur Verfügung. Die variablen Stückkosten von P1 bzw. P2 betragen
160 GE bzw. 200 GE. Für P2 kann ein Stückpreis von 300 GE erzielt werden. Der für P1
erzielbare Stückpreis p lässt sich aufgrund intensiver Preiskämpfe am Markt derzeit nicht
genau abschätzen; man kann lediglich sagen, dass p im Intervall [160, 220] liegt.
Das Unternehmen steht nun vor dem Problem, einen deckungsbeitragsmaximalen
Produktionsplan (d. h. die von P1 bzw. P2 zu produzierenden Stückzahlen x1 und x2) zu
bestimmen. Ermitteln Sie die Lösung
a. nach der Maximin-Regel,
b. nach der Maximax-Regel,
c. nach dem HURWICZ-Kriterium mit Optimismus-Parameter  = 23 .
11.
Gegeben ist eine Entscheidungssituation mit vier unscharf beschriebenen Alternativen ai, drei
möglichen Zuständen sj und der nachstehenden Ergebnismatrix Z  (z ij ) i 1,,4 .
j1,,3
s1
s2
s3
a1
(-90; -80; -60; -50; -30; -20)
(150; 160; 170; 190; 210; 220)
(30; 35; 40; 45; 50; 60)
a2
(-40, -30; -20; -10; 0; 10)
(130; 135; 150; 150; 160; 165)
(70; 75; 80; 90; 95; 100)
a3
(10; 20; 30; 30; 40; 50)
(90; 100; 105; 110; 120; 130)
(50; 60; 70; 80; 90; 100)
a4
(-60; -55; -50; -40; -35; -30)
(200; 220; 230; 240; 250; 270)
(-15; -10; 0; 10; 15; 25)
a. Wenden Sie
 die Maximin-Regel,
 die Maximax-Regel,
 das HURWICZ-Kriterium mit  = 0,7,
 das LAPLACE-Kriterium,
 die SAVAGE-NIEHANS-Regel und
 das KRELLE-Prinzip mit ( u )  3u  1  1
jeweils zur Auswahl einer Alternative (auf Basis der -Präferenz) an.
b. Man gehe nun davon aus, dass eine Entscheidungssituation unter Risiko vorliegt. Folgende
Eintrittswahrscheinlichkeiten der Zustände sj sind bekannt:
p1 = 0,3 p2 = 0,4 p3 = 0,3.
Welche Alternative wird ein risikoscheuer Entscheider wählen, wenn er die
Nutzenfunktion u( x )  x  90 seiner Entscheidung zugrunde legt.
4
12.
Eine ET besitzt eine lineare Nutzenfunktion. Bei einem Lotteriespiel kann sie 500 € mit der
Wahrscheinlichkeit w und 100 € mit der Wahrscheinlichkeit 1 - w gewinnen.
Wie groß ist die Wahrscheinlichkeit w, wenn das Sicherheitsäquivalent 400 € beträgt?
13.
Einem Unternehmer werden zwei Projekte angeboten. Bei dem ersten ist der Gewinn 20.000 €
oder 40.000 € jeweils mit der Wahrscheinlichkeit von 50%; bei dem zweiten erhält er jeweils
mit der Wahrscheinlichkeit von 50% einen Gewinn von y € bzw. 0 €.
Wie groß muss der Gewinn y des zweiten Projekts sein, damit beide Projekte gleich
eingeschätzt werden? Bei der Beantwortung kann davon ausgegangen werden, dass sich der
Unternehmer (in dem relevanten Bereich) gemäß der quadratischen Nutzenfunktion
x2
verhält.
u( x )  
 2x
100.000
14.
Ein Unternehmer ist Pessimist. Ein Projekt, bei dem er mit 50% Wahrscheinlichkeit einen Gewinn von x € erwarten kann, mit 50% Wahrscheinlichkeit dagegen nichts erhält, schätzt er
genauso ein wie ein Projekt, bei dem er 0,25x € mit Sicherheit bekommt. Dies gilt für jeden
beliebigen (positiven) Gewinn x.
Sein Unternehmen verkauft u. a. ein Waschmittel, das einen sicheren Platz auf dem Markt hat.
Im betrachteten Planungszeitraum könnte man 1.200.000 kg zu 3 € je kg absetzen. Die fixen
Kosten würden dabei 200.000 € betragen, die variablen Kosten würden sich auf 2 € je kg
belaufen.
In der Forschungsabteilung hat man ein besseres Waschmittel entwickelt, das das alte ersetzen
könnte. Marktforschungen haben ergeben, dass mit 25% Wahrscheinlichkeit damit zu rechnen
ist, dass das neue Produkt ein Verkaufsschlager wird. In diesem Fall rechnet die MarketingAbteilung für den betrachteten Planungszeitraum mit einem Absatz von 1.700.000 kg, im
anderen Fall nur mit 200.000 kg. Die fixen Kosten werden bei 250.000 € liegen, als
Absatzpreis könnte man 3,50 € pro kg fordern; die variablen Kosten belaufen sich nur auf 1 €
je kg.
Der Unternehmer steht vor der Frage, ob er weiterhin das alte Produkt verkaufen oder ob er
das neue Produkt auf den Markt bringen soll. Wie wird er sich entscheiden?
(Lösungshinweis: Führen Sie eine Normierung so durch, dass u(0) = 0 und u(1.000.000) = 1
gilt.)
15.
Herr Huber und Herr Meier bekommen ein Spiel angeboten, das mit 64%iger
Wahrscheinlichkeit eine Auszahlung von 10 € liefert. Im anderen Fall ist die Auszahlung
Null. Herr Huber handelt (für positive Ergebnisse x) nach der Nutzenfunktion uH(x)=2x²+5,
Herr Meier nach uM(x)=4x²+12.
Welches Sicherheitsäquivalent hat das Spiel
a. für Herrn Huber?
b. für Herr Meier?
c. Wie erklärt sich das Verhältnis beider Ergebnisse?