Entscheidung bei Unsicherheit i.e.S.

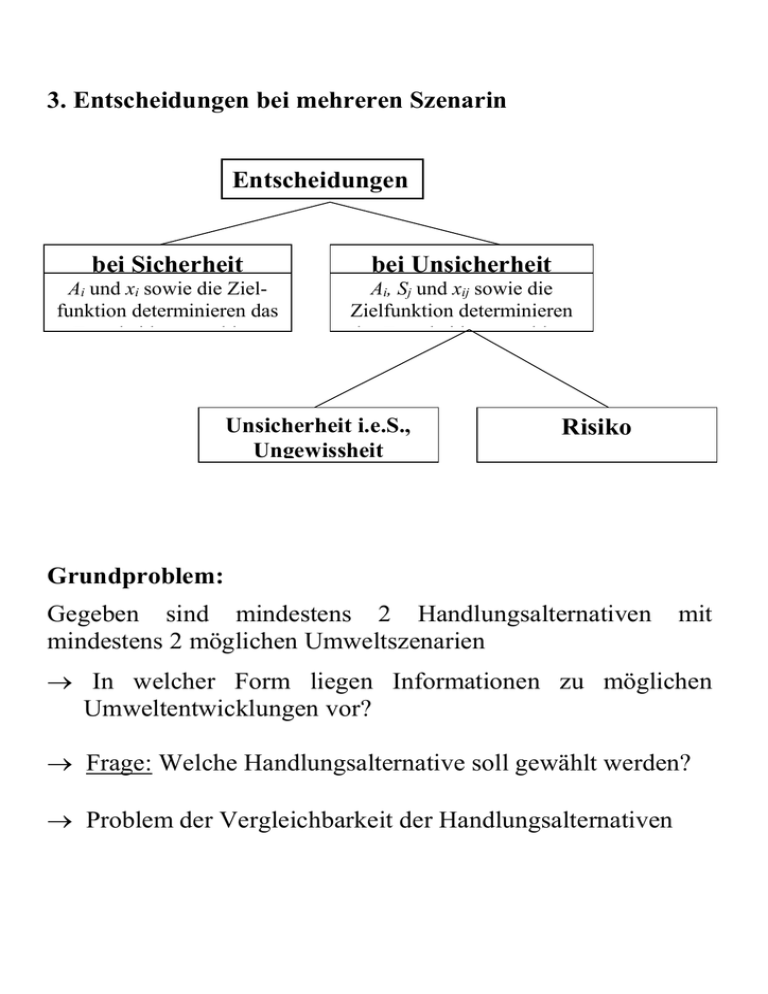
3. Entscheidungen bei mehreren Szenarin
Entscheidungen
bei Sicherheit
bei Unsicherheit
Ai und xi sowie die Zielfunktion determinieren das
Entscheidungsproblem
Ai, Sj und xij sowie die
Zielfunktion determinieren
das Entscheidungsproblem
Unsicherheit i.e.S.,
Ungewissheit
Risiko
Grundproblem:
Gegeben sind mindestens 2 Handlungsalternativen
mindestens 2 möglichen Umweltszenarien
mit
 In welcher Form liegen Informationen zu möglichen
Umweltentwicklungen vor?
 Frage: Welche Handlungsalternative soll gewählt werden?
 Problem der Vergleichbarkeit der Handlungsalternativen
3.1 Entscheidung bei Ungewißheit
 Wahrscheinlichkeiten für das Eintreten der relevanten
Umweltzustände sind unbekannt.
DOMINANZ-Prinzip
d.h. das Entscheidungsproblem wird
(=effiziente) Alternativen beschränkt
auf
undominierte
dominante Alternative:
Eine Alternative, die in allen Umweltzuständen genauso gut ist
wie alle anderen möglichen Alternativen, aber in mindestens
einem Umweltzustand besser abschneidet.
 bei Existenz einer dominanten HA = eindeutige Entscheidung
inferiore Alternative:
Eine Alternative, die in allen Umweltzuständen genauso gut ist
wie eine andere mögliche Alternative, aber in mindestens einem
Umweltzustand schlechter abschneidet,
(Alternative wird dominiert.)
 ausreichend, wenn Inferiorität gegenüber einer Alternative
besteht,
 inferiore HA werden im weiteren Entscheidungsprozeß nicht
weiter berücksichtigt
 Problem: meist noch keine eindeutige Entscheidung, da
weitere undominierte Alternativen bleiben
 zur weiteren Bestimmung der optimalen HA:
klassische Entscheidungsregeln !!
Maximin-Regel (WALD-Regel)
"Wähle die Alternative, die von den schlechtesten möglichen
Ergebnissen bzw. Nutzenwerten das beste aufweist!"
(a k )  max min u ij
i
j
 ordinale Nutzenfunktion
 Unterstellung von extremer Risikoscheu, da jeweils nur das
schlechteste Ergebnis berücksichtigt wird
Maximax-Regel
"Wähle die HA, die von den besten möglichen Ergebnissen das
höchste aufweist!"
(ak )  max max u ij
i
j
 ordinale Nutzenfunktion
 da nur jeweils das günstigste aller möglichen Ergebnisse
berücksichtigt wird, impliziert diese Regel eine extrem
optimistische (und damit auch risikofreudige) Einstellung
Hurwicz-Prinzip
"Bewerte das beste Ergebnis einer Alternative mit dem
subjektiv gewählten Optimismusindex  und das schlechteste
Ergebnis der Alternative mit 1 - .
Wähle dann die Aktion, die den größten gewichteten
Durchschnitt aus bestem und schlechtestem Ergebnis aufweist!"
 (a k )  max (  max u ij  (1   )  min u ij )
i
j
j
 je größer  gewählt wird, desto stärker gibt die günstigste
Handlungskonsequenz den Ausschlag für die Beurteilung von
ai   = Optimismusparameter
 je nach Wahl von  werden unterschiedliche HA ausgewählt
 Bestimmung von   [0, 1] muß individuell von jedem
Entscheider festgelegt werden;
 Hurwicz-Prinzip ist ein "Kompromiß" zwischen Minimax
und Maximax;
 = 1 – Maximax-Regel;
 = 0 – Maximin-Regel
Kritik:
a1
a2
z1 z2 z3 z4 z5 z6 . . . z1000
1 0 0 0 0 0 . . . 0
0 1 1 1 1 1 . . . 1
 beide Alternativen gleichwertig!!??
LAPLACE-Regel
"Bilde für jede Alternative die Summe der Ergebnisse und
wähle die Alternative, die die höchste Summe aufweist."
n
(a k )  max  u ij
i
j1
Vorteil: Gesamtheit der Ergebnisse wird in Berechnung
miteinbezogen.
Problem: Die Höhe der Wahrscheinlichkeiten, die einem
Umweltzustand zugeordnet wird, wird durch die
Abgrenzung der betrachteten Zustände bestimmt.
S1
S2
S1
S2
S3
A1
5
2
5
2
2
A2
-1
6
-1
6
6
 Transformation in Risikosituation?
SAVAGE-NIEHANS-Regel
 Bilde die Opportunitätskostenmatrix Kij gemäß
K ij  max u rj  u ij
r
(Kij = Nutzenentgang, regret)
 Bestimme die optimale Alternative durch Anwendung der
Maximin-Regel auf Kij
 (a k )  min max ( max u rj  u ij )
i
j
r
kardinale Nutzenfunktion notwendig!!
Beispiel: 5 Alternativen, 4 Umweltzustände,
uij = alternative Einkommensbeträge
Ziel des Entscheiders: möglichst hohes Einkommen
a1
a2
a3
a4
a5
s1
s2
s3
s4
100
20
85
110
10
0
10
3
10
5
0
20
3
-20
15
0
30
4
0
30
Minimax Maximax
Hurwicz
 = 0,15
Laplace
s1
s2
s3
s4
a1
100
0
0
0
a2
20
10
20
30
a3
85
3
3
4
a4
110
10
-20
0
a5
10
5
15
30
s3
s4
SavageNiehans
Opportunitätskostenmatrix
Kij
a1
a2
a3
a4
a5
s1
s2
3.1.2 Fuzzy-Bewertungen in Ungewißheitssituationen
s1
s2
s3
a1
(170; 180; 200;
220; 225; 230)
(70; 83; 90; (-110; -97; -90;
100; 110; 120) -77; -60, -50)
a2
(140; 155; 165;
175; 180; 190)
(8 5; 93; 100; (-85; -80; -70; 110; 115; 125) 58; -50; -40)
a3
(120; 135; 145; (115; 130; 135; (-30; -20; -10;
150; 160; 170) 140; 145; 150)
0; 5; 10)
a4
(85; 90; 100;
110; 115; 125)
a5
(45; 48; 50;
53; 58; 60)
a6
(85; 93; 100; (-15; -10; -5;
105; 108; 115)
5; 10; 15)
(40; 45; 50;
50; 53; 55)
(35; 40; 45;
50; 55; 60)
(105; 110; 125; (100; 110; 125; (-40; -30; -20;
135; 145; 150) 135; 140; 145)
-10; 0; 10)
Umweltabhängige Fuzzy-Ergebnisse
 Übertragung des Dominanzprinzips und der Entscheidungsregeln möglich ?!
 Dominanzprinzip
 Maximum-/Minimumbildung
< 3.5 >
~
A  (5; 7; 9; 9;12;13), und
~
B  (6; 6,5; 8,5; 11;13;14), .
 nach dem Erweiterungsprinzip gilt
~ ~~
M i n( A,B)  (5; 6,5; 8,5;11;12;13), und
~~
M~
a x( A,B)  (6; 7; 9;11;13;14), ,
 Ergebnisse, die nicht real vorliegen,
d.h. keine wirkliche Aktionsoption
~
ax "
 Verwendung der Operatoren " R  M i n " und " R  M~
~ ~
~
~
A q = R  M i n ( A1 ,, A n )
~
~
 Aq  A j
~
~
~
a x ( A1 ,, A n )
A p = R  M~
~
~
 Ap A j
für alle j = 1,..., n
für alle j = 1,...,
n
~ ~ ~ ~
 R  M i n ( A, B) = A  (3; 5; 7; 9; 10; 11) , und
~ ~ ~
a x ( A, B) = B  (4; 4,5; 6,5; 9; 11; 12) , 
 R  M~
Für
~
C  (2; 3; 4; 7; 8; 10)
und

D  (3,5; 5; 6; 6,5; 7; 8)
 objektiv nicht möglich, eine Rangfolge festzulegen.
 Übertragung der Maximum- und Minimumbildung:
Wahl des besten/schlechtesten Ergebnisses unter den relevanten Ergebnissen in Abhängigkeit von der gewählten
Präferenzrelation
(-Präferenz  Niveau-Ebenen-Verfahren)
Maximin-Regel
~ ~
~
a x ( R  M i n U ij )
 (a k ) = R  M~
i
j
Maximax-Regel
~
~
a x ( R  M~
 (a k ) = R  M~
a x U ij )
i
j
HURWICZ-Regel
~ ~
~
~
a x U ij + (1 - ) R  M i n U ij ]
 (a k ) = R  M~
a x [ R  M~
j
i
LAPLACE-Regel
~
~
a x 1  U ij
 (a k ) = R  M~
i
n
j
j
s1
a2
a3
a4
a5
s3
a1
(170; 180; 200;
220; 225; 230)
(70; 83; 90; (-110; -97; -90;
100; 110; 120) -77; -60, -50)
a2
(140; 155; 165;
175; 180; 190)
(8 5; 93; 100; (-85; -80; -70; 110; 115; 125) 58; -50; -40)
a3
(120; 135; 145; (115; 130; 135; (-30; -20; -10;
150; 160; 170) 140; 145; 150)
0; 5; 10)
a4
(85; 90; 100;
110; 115; 125)
a5
(45; 48; 50;
53; 58; 60)
Maximin
a1
s2
(85; 93; 100; (-15; -10; -5;
105; 108; 115)
5; 10; 15)
(40; 45; 50;
50; 53; 55)
Maximax
(35; 40; 45;
50; 55; 60)
HURWICZ
=0,5
s1
s2
s3
a1
(170; 180; 200;
220; 225; 230)
(70; 83; 90; (-110; -97; -90;
100; 110; 120) -77; -60, -50)
a2
(140; 155; 165;
175; 180; 190)
(8 5; 93; 100; (-85; -80; -70; 110; 115; 125) 58; -50; -40)
a3
(120; 135; 145; (115; 130; 135; (-30; -20; -10;
150; 160; 170) 140; 145; 150)
0; 5; 10)
a4
(85; 90; 100;
110; 115; 125)
a5
(45; 48; 50;
53; 58; 60)
(85; 93; 100; (-15; -10; -5;
105; 108; 115)
5; 10; 15)
(40; 45; 50;
50; 53; 55)
(35; 40; 45;
50; 55; 60)
LAPLACE
a1
(43,33; 55,33; 66,67; 81; 91,67; 100)
a2
(46,67; 56; 65; 75,67; 81,67; 91,67)
a3
(68,33; 81,67; 90; 96,67; 103,33; 110)
a4
(51,67; 57,67; 65; 73,33; 77,67; 85)
a5
(40; 44,33; 48,33; 51; 55,33; 58,33)
SAVAGE-NIEHANS-Regel
 Bestimmung der Opportunitätskostenmatrix aus unscharfen
Nutzenwerten ??!!
 direkte Fuzzifizierung der Formel mittels erweiterter
Subtraktion
~
~
~
K ij = R  M~
a x U rj  U ij
r
(a  , a  , a 1 , a 1 , a  , a  ) ,  ( b ,b ,b1, b1, b , b ), =
(a   b , a   b , a1  b1, a1  b1, a   b , a   b ),
Beispiel:
 Bestimmung des Nutzenentgangs durch "Subtraktion der
~ ~ ~
Tupel" aus A  C  B
 Problem: evtl. Fuzzy-Größe mit Zahlen in nicht (schwach)
aufsteigender Reihenfolge
~
~
 "Subtraktionsvariante" für A   B aus

~ ~
~
AC  B
 ( a  , a  , a 1 , a 1 , a  , a  ) + ( c  , c  , c1 , c 1 , c  , c  ) 
( b  , b  , b1 , b1 , b  , b  )
mit c   c   c1  c 1  c   c 
 gilt wenn
c = b  a 
c
= Max {cR| c  b   a  und c  c  }
c1
= Max {cR| c  b1  a 1 und c  c  }
c1
= Max {cR| c  b1  a 1 und c  c 1 }
c
= Max {cR| c  b  a  und c  c1}
c
= Max {cR| c  b   a  und c  c  }
a1
a2
a3
a4
A5
s1
s2
s3
(0; 0; 0;
0; 0; 0)
(25; 25; 35;
40; 40; 40)
(45; 45; 55;
60; 60; 60)
(85; 90; 100;
105; 105; 105)
(125; 138; 150;
167; 167; 170)
(30; 30; 30;
30; 30; 30)
(25; 25; 25;
25; 25; 25)
(0; 0; 0;
0; 0; 0)
(30; 35; 35;
35; 35; 35)
(75; 85; 85;
90; 92; 95)
(110; 110; 110;
110; 110, 110)
(100; 100; 100;
100; 100; 100)
(50; 50; 50;
50; 50; 50)
(45; 45; 45;
45; 45; 45)
(0; 0; 0;
0; 0; 0)
Opportunitätskostenmatrix
 Bestimmung der optimalen Aktion
~
~
~
a x C ij ]
 (a k ) = R  M i n [ R  M~
i
j
 hier: optimale Alternative
 Entscheidungsregeln unter Ungewißheit anwendbar, auch
wenn Ergebnisse nur ungefähr bekannt sind,
 keine Notwendigkeit, Daten künstlich unter Kostenaufwendung zu verschärfen
 Problem: Optimale Alternative abhängig von angewendeter
Entscheidungsregel??!!
Resumee
reale Entscheidungssituationen werden eher unter der Annahme
von Risiko gelöst
 Unsicherheit i.e.S. hat kaum praktische Relevanz,
da Entscheider fast immer aus Erfahrung oder aufgrund von
Information gewisse Glaubwürdigkeitsvorstellungen über
bestimmte Umweltentwicklungen hat
 Eintrittswahrscheinlichkeiten;
selbst bei keiner Information ist Unterstellung von
Gleichwahrscheinlichkeit nicht sinnvoll, da bestimmte
Umweltzustände unwahrscheinlicher sind als andere