Intermediate Microeconomics Aufgabenblatt 2

Georg Nöldeke
Herbstsemester 2010
Intermediate Microeconomics
Aufgabenblatt 2
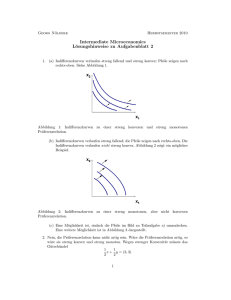
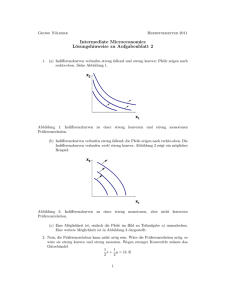
1. Zeichnen Sie jeweils einige Indifferenkurven, welche die folgenden Eigenschaften einer
rationalen Präferenzrelation erkennen lassen. Verwenden Sie dabei jeweils Pfeile, um
darzustellen, in welcher Richtung die Güterbündel liegen, die denen auf einer Indifferenzkurve streng vorgezogen werden.
(a) Die Präferenzrelation ist streng konvex und streng monoton.
(b) Die Präferenzrelation ist streng monoton, aber nicht konvex.
(c) Die Präferenzrelation ist weder konvex noch monoton.
2. Die Güterbündel x = (2, 5), y = (4, 1) und z = (3, 4) liegen auf einer Indifferenzkurve
einer Präferenzrelation. Kann diese Präferenzrelation artig sein?
3. Bestimmen Sie für die folgenden Nutzenfunktionen die Grenznutzen der beiden Güter
und die Grenzrate der Substitution für Güterbündel x = (x1 , x2 ) mit x1 > 0 und
x2 > 0 (d.h. es sind nur innere Güterbündel zu betrachten). Geben Sie an, welche der
Nutzenfunktionen artig sind.
(a) u(x1 , x2 ) = ax1 + x2 mit a > 0.
√
(b) u(x1 , x2 ) = 2a x1 + x2 mit a > 0
(c) u(x1 , x2 ) = (x1 − a)(x2 − b) mit a > 0 und b > 0
4. Verschiedene artige Nutzenfunktionen stellen genau dann die gleiche Präferenzrelation
dar, wenn das Verhältnis ihrer jeweiligen Grenznutzen für alle inneren Güterbündel
übereinstimmt. Verwenden Sie diese Tatsache, um zu zeigen, dass die Nutzenfunktion
u(x1 , x2 ) = Axc1 xd2 mit A > 0, c > 0, d > 0 die gleiche Präferenzrelation wie die
c/(c+d) d/(c+d)
Nutzenfunktion v(x1 , x2 ) = x1
x2
darstellt.
5. Die Präferenzrelation einer Konsumentin wird durch die Nutzenfunktion
u(x1 , x2 ) = a ln(x1 ) + x2 mit a > 0
dargestellt. Bestimmen Sie die Nachfragefunktion der Konsumentin. Hinweis: Bedenken Sie, dass die Konsumentin nicht mehr als ihr Einkommen m für Gut 1 ausgeben
kann.
6. Die Präferenzrelation eines Konsumenten kann durch die Nutzenfunktion
u(x1 , x2 ) = x1 + 4x2
dargestellt werden. Das Budget des Konsumenten ist m = 120.
(a) Welches Güterbündel ist bei (p1 , p2 ) = (5, 24) optimal?
(b) Wie ändert sich die Lösung des Nutzenmaximierungsproblems, wenn der Preis
von Gut 2 auf p2 = 15 fällt?
(c) Machen Sie sich die Lösungen grafisch klar, indem Sie die entsprechenden Budgetgeraden und Indifferenzkurven darstellen.
1
7. Betrachten Sie die Nachfragefunktion
f1 (p1 , p2 , m) =
m
m
mit r ≥ 0.
1−r r , f2 (p1 , p2 , m) =
p1 + p2 p1
p2 + p1−r
pr2
1
(a) Bestimmen Sie die Einkommenselastizität der beiden Güter. Sind die Güter normal oder inferior?
(b) Für welche Werte von r sind die Güter Komplemente für einander? Für welche
Werte von r sind sie Substitute für einander? Hinweis: Es ist nicht erforderlich, dass sie die Kreuzpreiselastizitäten berechnen - es genügt ihr Vorzeichen zu
bestimmen.
8. Die Nachfragefunktion einer Konsumentin ist für Preise und Einkommen, für welche
m + 1 > p2 > 1 gilt, durch
x1 = f1 (p1 , p2 , m) =
1
m − p2 + 1
, x2 = f2 (p1 , p2 , m) = 1 −
p1
p2
gegeben. Erfüllt diese Nachfragefunktion die Budgetidentität? Ist sie homogen vom
Grad Null in Preisen und Budget?
9. Bei Preisen (p1 , p2 ) = (5, 5) und Einkommen m = 100 fragt ein Konsument das
Güterbündel (x1 , x2 ) = (12, 8) nach. Bei Preisen (p̃1 , p̃2 ) = (4, 8) und Einkommen
m̃ = 116 ist seine Nachfrage (x̃1 , x̃2 ) = (9, 10). Erklären Sie, wieso dieses Verhalten
nicht mit der Annahme verträglich ist, dass die Nachfragefunktion des Konsumenten
artig ist. Hinweis: Zeigen Sie einen Widerspruch zu der Annahme, dass die nachgefragten Güterbündel die eindeutigen Lösungen des Nutzenmaximierungsproblems in
der jeweiligen Budgetmenge sind.
10. Bei gegebenen Peisen und Budget beträgt der Ausgabenanteil eines Gutes θi = 0.2.
Die Einkommenselastizität ist ξi = −0.4, die Substitutionselastizität ist ∗ii = −0.07.
Ist das Gut gewöhnlich oder Giffen?
11. Betrachten Sie den Fall der perfekten Komplemente mit Nutzenfunktion u(x1 , x2 ) =
min{x1 , x2 }.
(a) Bestimmen Sie die indirekte Nutzenfunktion U (p, m) und die Ausgabenfunktion
E(p, ū).
(b) Bestimmen Sie die kompensierte Nachfragefunktion h(p, ū). Wie gross ist hier die
Substitutionselastizität der beiden Güter?
(c) Ein Konsument mit der betrachteten Nutzenfunktion hat in einer Ausgangssituation das Budget m = 120; die Güterpreise sind (p1 , p2 ) = (2, 3). Nun steigt
der Preis von Gut 1 auf p∗1 = 4. Um welchen Betrag müsste das Einkommen des
Konsumenten erhöht werden, um ihn für diesen Preisanstieg zu kompensieren?
12. Eine Konsumentin mit artiger Präferenzrelation hat im Jahre 2008 das Güterbündel
(xb1 , xb2 ) = (32, 50) bei Preisen von (pb1 , pb2 ) = (25, 16) konsumiert.
(a) Im Jahr 2009 beträgt ihr Einkommen mt = 1620; die Güterpreise sind (pt1 , pt2 ) =
(36, 9). Können Sie sagen, in welchem der Jahre es der Konsumentin besser geht?
(b) Unterstellen Sie, dass sich die Präferenzen der Konsumentin durch eine CobbDouglas-Nutzenfunktion beschreiben lassen. Wie hoch müsste ihr Einkommen in
2009 sein, damit es ihr in beiden Jahren gleich gut geht?
2
13. In der Vorlesung wurde argumentiert, dass eine Mengensteuer auf ein Gut einen Konsumenten schlechter als eine Kopfsteuer stellt, die zu den gleichen Steuereinnahmen
führt. Was gilt für den entsprechenden Vergleich einer Mengensubvention und einer
Kopfsubvention, die dazu führen, dass der Konsument die gleiche Subventionszahlung
erhält? Fertigen Sie hierzu eine geeignete Abbildung an.
14. Betrachten Sie einen Konsumenten mit quasilinearer Nutzenfunktion
√
u(x1 , x2 ) = 16 x1 + x2 .
Gut 2 ist Numeraire. Das Einkommen des Konsumenten sei m = 200. Der Preis von
Gut 1 steigt von p1 = 1 auf p∗1 = 4. Bestimmen Sie die Änderung der Konsumentenrente.
3