Lösungen

Georg Nöldeke
Herbstsemester 2010
Intermediate Microeconomics
Lösungshinweise zu Aufgabenblatt 2
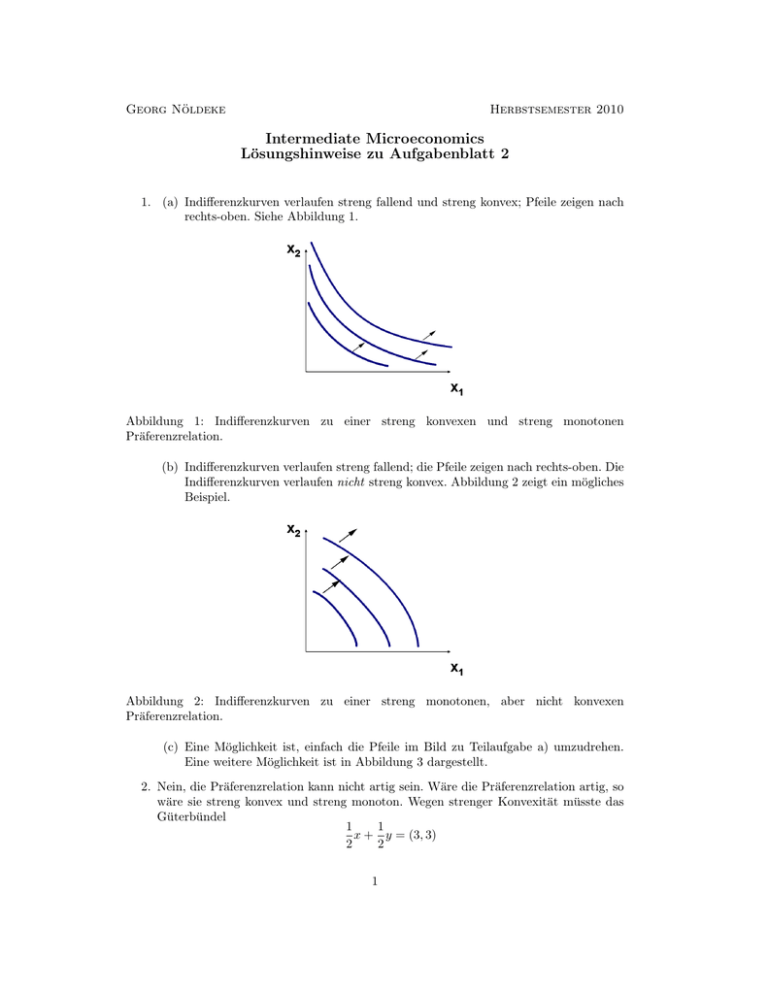
1. (a) Indifferenzkurven verlaufen streng fallend und streng konvex; Pfeile zeigen nach
rechts-oben. Siehe Abbildung 1.
Abbildung 1: Indifferenzkurven zu einer streng konvexen und streng monotonen
Präferenzrelation.
(b) Indifferenzkurven verlaufen streng fallend; die Pfeile zeigen nach rechts-oben. Die
Indifferenzkurven verlaufen nicht streng konvex. Abbildung 2 zeigt ein mögliches
Beispiel.
Abbildung 2: Indifferenzkurven zu einer streng monotonen, aber nicht konvexen
Präferenzrelation.
(c) Eine Möglichkeit ist, einfach die Pfeile im Bild zu Teilaufgabe a) umzudrehen.
Eine weitere Möglichkeit ist in Abbildung 3 dargestellt.
2. Nein, die Präferenzrelation kann nicht artig sein. Wäre die Präferenzrelation artig, so
wäre sie streng konvex und streng monoton. Wegen strenger Konvexität müsste das
Güterbündel
1
1
x + y = (3, 3)
2
2
1
Abbildung 3: Indifferenzkurven zu einer Präferenzrelation, die weder konvex noch monoton
ist.
dem Güterbündel y (und auch x) streng vorgezogen werden. Aus strenger Monotonie der Präferenzrelation würde dann folgen, dass das Güterbündel z = (3, 4) dem
Güterbündel (3, 3) streng vorgezogen wird. Also müsste (Transitivität der Präferenzrelation)
z y gelten. Dieser Widerspruch zu der Annahme z ∼ y zeigt, dass die Präferenzrelation
nicht artig sein kann. Siehe Abbildung 4.
Abbildung 4: Liegen (2, 5), (3, 4) und (4, 1) auf einer Indifferenzkurve, kann die
Präferenzrelation nicht artig sein.
3. Hinweis: Die Grenznutzen sind die partiellen Ableitungen der Nutzenfunktion. Um die
partielle Ableitung nach x1 zu bestimmen, betrachtet man x2 als Konstante und bildet
die Ableitung der resultierenden Funktion von x1 . Entsprechend bestimmt man die
partielle Ableitung nach x2 , indem man x1 als Konstante betrachtet und die Ableitung
der resultierenden Funktion von x2 bestimmt.
Zur Abkürzung der Schreibweise werden in den Antworten auf diese Aufgabe die Grenznutzen mit
∂u(x1 , x2 )
∂u(x1 , x2 )
u1 (x) :=
und u2 (x) :=
∂x1
∂x2
bezeichnet. Die Grenzrate der Substitution ist dann also jeweils durch
GRS(x) = −
gegeben.
2
u1 (x)
u2 (x)
(a) Es handelt sich um perfekte Substitute. Die Grenznutzen sind
u1 (x) = a und u2 (x) = 1.
Die Grenzrate der Substitution ist also
GRS(x) = −a.
Die Nutzenfunktion ist nicht artig, da die Grenzrate der Substitution konstant
ist.
(b) Es handelt sich um eine quasilineare Nutzenfunktion. Die Grenznutzen sind
a
u1 (x) = √ und u2 (x) = 1.
x1
Die Grenzrate der Substitution ist also
a
GRS(x) = − √ .
x1
Die Nutzenfunktion ist artig, da das Verhältnis der Grenznutzen (der Absolutwert
der Grenzrate der Substitution) streng fallend in x1 und unabhängig von x2 ist.
Abbildung 5: Niveaulinien der Nutzenfunktion u(x1 , x2 ) =
√
x1 + x2 .
(c) Die Grenznutzen sind
u1 (x) = x2 − b und u2 (x) = x1 − a.
Die Grenzrate der Substitution ist also für x1 = a nicht definiert und ansonsten
durch
x2 − b
GRS(x) = −
x1 − a
gegeben. Die Nutzenfunktion ist nicht artig, da die Grenznutzen für x1 < a bzw.
für x2 < b negativ sind.
3
4. Mit der gleichen Notation fur die Grenznutzen wie in Aufgabe 3:
d
c d−1
u1 (x) = Acxc−1
1 x2 und u2 (x) = Adx1 x2
sowie
v1 (x) =
c
d
c/(c+d)−1 d/(c+d)
c/(c+d) d/(c+d)−1
x
x
x2
x2
und v2 (x) =
.
c+d 1
c+d 1
Nun gilt
c x2
c/(c + d) x2
v1 (x)
u1 (x)
=
=
=
,
u2 (x)
d x1
d/(c + d) x1
v2 (x)
so dass die Verhältnisse der Grenznutzen übereinstimmen.
5. Es handelt sich um eine quasilineare Nutzenfunktion mit v(x1 ) = a ln x1 . Da
v 0 (x1 ) =
a
a
> 0, v 00 (x1 ) = − 2 < 0,
x1
x1
ist die Nutzenfunktion artig. (Siehe dazu auch Abbildung 6, welche die Niveaulinien
der Nutzenfunktion für den Fall a = 1 darstellt.)
Abbildung 6: Niveaulinien der Nutzenfunktion u(x1 , x2 ) = ln(x1 ) + x2 .
Da es sich um eine artige quasilineare Nutzenfunktion handelt, gilt in einer inneren
Lösung des Nutzenmaximierungsproblems v 0 (x1 ) = p1 /p2 und somit
x1 =
ap2
> 0.
p1
Setzt man diesen Wert von x1 in die Budgetgerade ein, erhält man ap2 + p2 x2 = m
und somit
m
x2 =
− a.
p2
4
Gilt m ≥ ap2 ist dieser Wert von x2 positiv, so dass die Lösung des Nutzenmaximierungsproblems identifiziert ist. Gilt hingegen m < ap2 , so übersteigen die Ausgaben
für x1 das Budget. In diesem Fall handelt es sich bei der Lösung des Nutzenmaximierungsproblems um eine Randlösung mit x1 = m/p1 und x2 = 0, d.h. das gesamte
Budget wird für Gut 1 ausgegeben.
Die obige Fallunterscheidung kann man dadurch erfassen, dass man die Nachfragefunktion als
f1 (p1 , p2 , m) =
m
min{ap2 , m}
, f2 (p1 , p2 , m) = max{ − a, 0}
p1
p2
schreibt.
6. Es handelt sich um perfekte Substitute, bei denen die marginale Zahlungsbereitschaft
für Gut 1 durch a = 1/4 gegeben ist.1
(a) Da der relative Preis 5/24 hier streng kleiner als die marginale Zahlungsbereitschaft 1/4 ist, wird der Konsument sein gesamtes Budget für Gut 1 ausgeben.
Das optimale Güterbündel ist also (24, 0).
(b) Der relative Preis steigt nun auf 5/15 = 1/3 > 1/4. Da der relative Preis streng
oberhalb der marginalen Zahlungsbereitschaft liegt, ist es optimal, das gesamte
Budget für Gut 2 auszugeben. Das optimale Güterbündel ist also (0, 8).
(c) Siehe Abbildung 7.
Abbildung 7: Die optimalen Güterbündel zu Aufgaben 6(a) und 6(b).
7. (a) Die Einkommenselastizität beider Güter ist kontant gleich 1: ξi (p, m) = 1. Insbesondere sind also beide Güter normal.
(b) Für r < 1 ist p1−r
steigend in p2 , so dass die Nachfrage von Gut 1 fällt, wenn der
2
Preis von Gut 2 steigt. Also ist in diesem Fall Gut 1 ein Komplement für Gut 2.
Entsprechend ist auch Gut 2 ein Komplement für Gut 1.
1 Die angegebene Nutzenfunktion stellt die gleiche Präferenzrelation wie die Nutzenfunktion v(x , x ) =
1
2
0.25x1 + x2 dar.
5
Für r = 1 hängt die Nachfrage von Gut i nicht von dem Preis von Gut j 6= i ab,
so dass die Güter weder Komplemente noch Substitute für einander sind.
Für r > 1 ist p1−r
fallend in p2 , so dass die Nachfrage von Gut 1 steigt, wenn
2
der Preis von Gut 2 steigt. Also ist in diesem Fall Gut 1 ein Substitut für Gut 2.
Entsprechend ist auch Gut 2 ein Substitut für Gut 1.
8. Die Budgetidentität ist hier erfüllt:
p1 f1 (p1 , p2 , m) + p2 f2 (p1 , p2 , m) = (m − p2 + 1) + (p2 − 1) = m.
Die Nachfragefunktion ist nicht homogen vom Grad Null in Preisen und Budget. Insbesondere gilt für t 6= 1:
f2 (tp1 , tp2 , tm) = 1 −
1
1
6= f2 (p1 , p2 , m) = 1 − .
tp2
p2
9. Da
x̃1 p1 + x̃2 p2 = 95 < m = 100
gilt, ist das Güterbündel (x̃1 , x̃2 ) in der Budgetsituation erschwinglich, in der (x1 , x2 )
nachgefragt wird. Resultiert das Nachfrageverhalten des Konsumenten aus der Maximierung einer artigen Nutzenfunktion u, so muss also
u(x1 , x2 ) > u(x̃1 , x̃2 )
gelten.
Zugleich gilt aber auch
x1 p̃1 + x2 p̃2 = 112 < m̃ = 116,
so dass das Güterbündel (x1 , x2 ) in der Bugetsituation erschwinglich ist, in der (x̃1 , x̃2 )
nachgefragt wird. Resultiert das Nachfrageverhalten des Konsumenten aus der Maximierung einer artigen Nutzenfunktion u, so müsste also auch
u(x̃1 , x̃2 ) > u(x1 , x2 )
gelten. Da nur eine der beiden Ungleichungen u(x1 , x2 ) > u(x̃1 , x̃2 ) und u(x̃1 , x̃2 ) >
u(x1 , x2 ) gelten kann, resultiert ein Widerspruch zu der Annahme, dass die Nachfragefunktion artig ist.
10. Auf Grund der Identität
ii = ∗ii − θi ξi
folgt aus den Angaben in der Aufgabenstellung ii = −0.07 + 0.08 = 0.01 > 0, so dass
die Eigenpreiselastizität der Nachfrage von Gut i streng positiv ist. Also ist das Gut
Giffen.
6
11. (a) Um die indirekte Nutzenfunktion zu bestimmen, setzt man das in der Budgetsituation (p, m) nachgefragte Güterbündel in die Nutzenfunktion sein. Hier ist das
nachgefragte Güterbündel
f1 (p1 , p2 , m) =
m
m
, f2 (p1 , p2 , m) =
.
p1 + p2
p1 + p2
Also:
U (p, m) = u(f (p, m)) = min{m/(p1 + p2 ), m/(p1 + p2 )} =
m
,
p1 + p2
so dass in diesem Beispiel die indirekte Nutzenfunktion mit der (für beide Güter
identischen) nachgefragten Menge übereinstimmt.
Um die Ausgabenfunktion zu bestimmen, kann man das Ausgabenminimierungsproblem lösen oder aber die Gleichung ū = U (p, m) nach m = E(p, ū) auflösen.
Da hier die indirekte Nutzenfunktion bereits bestimmt ist, ist der zweite Weg
einfacher:
m
⇒ m = ū (p1 + p2 ) ,
ū =
p1 + p2
so dass die Ausgabenfunktion
E(p, ū) = ū (p1 + p2 )
ist.
(b) Um die kompensierte Nachfragefunktion zu bestimmen, kann (i) man das Ausgabenminimierungsproblem lösen oder (ii) die Ausgabenfunktion für das Einkommen in die unkompensierte Nachfragefunktion einsetzen oder (iii) Shepards
Lemma verwenden. Die zweite und dritte Möglichkeit setzen voraus, dass man die
Ausgabenfunktion bereits bestimmt hat. Dieses ist hier der Fall und man erhält
so oder so:
h1 (p, ū) = h2 (p, ū) = ū.
Dieses Ergebnis bedeutet einfach nur, dass in diesem Beispiel der billigste Weg
das Nutzenniveau ū zu erreichen, darin besteht von beiden Gütern genau die
Menge ū zu konsumieren.
Da die kompensierte Nachfragefunktion hier unabhängig von den Preisen ist, ist
die Substitutionselastizität beider Güter gleicht Null - es gibt keinen Substitutionseffekt.
(c) Hier ist die kompensierende Variation zu bestimmen. In der Ausgangssituation
wird das Nutzenniveau
ū = U (2, 3, 120) = 120/5 = 24
erreicht. Setzt man dieses Nutzenniveau zusammen mit den Preisen in der neuen
Situation in die Ausgabenfunktion ein, erhält man das Einkommen, das bei den
neuen Preisen erforderlich ist, um das Nutzenniveau ū zu erreichen. Dieses ist:
E(4, 3, 24) = 24 · 7 = 168.
Die Differenz zwischen E(4, 3, 24) und dem tatsächlichen Einkommen von 120
ergibt die kompensierende Variation:
CV = 168 − 120 = 48.
7
Da es in diesem Beispiel keinen Substitutionseffekt gibt, entspricht die erforderliche Einkommenskompensation gerade dem Betrag, der es dem Konsumenten
ermöglicht, dass in der Ausgangssituation gewählte Güterbündel weiterhin nachzufragen. Da der Konsument in der Ausgangssituation f1 (2, 3, 120) = 24 Einheiten von Gut 1 nachfragt und der Preis dieses Gutes um 2 Einheiten steigt, erhält
man auf diesem Wege ebenfalls die Antwort, dass die erforderliche Einkommenskompensation 48 Geldeinheiten beträgt.
12. (a) Da
pt1 xb1 + pt2 xb2 = 36 · 32 + 9 · 50 = 1152 + 450 = 1602 < mt1 = 1620
gilt, kann sich die Konsumentin das Güterbündel, welches sie in 2008 konsumiert
hat, in 2009 immer noch leisten. Also geht es ihr in 2009 besser. Beachte:
Könnte sie sich das in 2008 gewählte Güterbündel in 2009 nicht mehr leisten, so
kann daraus nicht ohne weiteres geschlossen werden, dass es ihr in 2008 besser
ging. Ein solcher Schluss wäre ohne weitere Informationen über die Präferenzen
nur möglich, wenn man wüsste, dass sie sich das in 2009 gewählte Güterbündel
in 2008 leisten konnte.
(b) Im Jahr 2008 gibt die Konsumentin für beide Güter den gleichen Betrag, nämlich
25 · 32 = 16 · 50 = 800 aus. Die Budgetanteile der Güter sind also jeweils 1/2, so
dass die Präferenzen der Konsumentin durch die Cobb-Douglas-Nutzenfunktion
√ √
u(x1 , x2 ) = x1 x2
mit dazugehöriger unkompensierter Nachfragefunktion
f1 (p1 , p2 , m) =
m
m
und f2 (p1 , p2 , m) =
2p1
2p2
dargestellt werden können. In der Aufgabenstellung ist nach der kompensierenden Variation der Preisänderung gefragt. Um diese zu bestimmen, berechne man
zunächst die indirekte Nutzenfunktion:
m
U (p1 , p2 , m) = u(f (p, m)) = √
.
2 p1 · p2
Die dazugehörige Ausgabenfunktion ist
√ √
E(p1 , p2 , ū) = 2 p1 p2 ū.
In der Ausgangssituation verfügt die Konsumentin über ein Budget von m = 1600
und erreicht das Nutzenniveau ū = U (25, 16, 1600) = 1600/40 = 40. Um das
gleiche Nutzenniveau im Jahr 2009 zu erreichen, benötigt die Konsumentin ein
Einkommen in Höhe von
E(36, 9, 40) = 2 · 6 · 3 · 40 = 1440.
(Zur Kontrolle kann man bemerken, dass die Konsumentin bei diesem Einkommen und den Preisen des Jahres 2009
√ das Güterbündel (20, 80) wählt und damit
tatsächlich den Nutzen u(x1 , x2 ) = 1600 = 40 erzielt.
13. Der Konsument wird durch die Kopfsubvention besser gestellt.
In der Ausgangssituation ohne jede Subventionen seien die Preise der beiden Güter
durch (p1 , 1) gegeben; das Einkommen des Konsumenten sei m.
8
Sei (x∗1 , x∗2 ) das Güterbündel, welches der Konsument bei einer Mengensubvention von
s > 0 pro Einheit von Gut 1 nachfragt. (Wie im Fall der Besteuerung ist unterstellt, dass die Einführung der Subvention den Preis p1 unverändert lässt.) Für dieses
Güterbündel gilt
(p1 − s)x∗1 + x∗2 = m ⇔ p1 x∗1 + x∗2 = m + sx∗1 ,
wobei sx∗1 die Subventionszahlung ist, die der Konsument erhält.
Wird statt der Mengensubvention die Kopfsubvention S = sx∗1 gezahlt, so gilt
p1 x∗1 + x∗2 = m + S,
so dass das Güterbündel (x∗1 , x∗2 ) bei Zahlung dieser Kopfsubvention erschwinglich
ist. Hieraus folgt, dass der Konsument durch die Kopfsubvention besser gestellt wird.
Dieses wird durch Abbildung 8 verdeutlicht.
Abbildung 8: Die Budgetgerade mit Kopfsubvention verläuft durch das Güterbündel (x∗1 , x∗2 )
(rot markiert), welches der Konsument in der Situation mit Mengensubvention wählt. Dieses
garantiert, dass der Konsument sich bei der Kopfsubvention zumindest gleich gut wie in
der Situation mit Mengensubvention stellt. Im Regelfall wird sich der Konsument streng
besser stellen, da er auf Grund des Substitutionseffekts bei der Kopfsubvention ein anderes
Güterbündel (hier pink markiert) wählt.
14. Es handelt sich um eine artige quasilineare Nutzenfunktion mit Zahlungsbereitschaft
√
v(x1 ) = 16 x1 . Da Gut 2 Numeraire ist, betrachten wir im Folgenden nur den Fall
p2 = 1.
In einer inneren Lösung des Nutzenmaximierungsproblems gilt v 0 (x1 ) = p1 , also
8
64
√ = p 1 ⇒ x1 = 2 .
x1
p1
9
Einsetzen von x1 in die Budgetgleichung liefert die dazugehörige Menge x2 :
64
+ x2 = m ⇒ x2 = m − 64/p1 .
p1
Setzt man m = 200 sowie p1 = 1 ein, erhält man (x1 , x2 ) = (64, 136) als Lösung des
Nutzenmaximierungsproblems. Entsprechend erhält man für p∗1 = 4 das Güterbündel
(x∗1 , x∗2 ) = (4, 184) als Lösung des Nutzenmaximierungsproblems.
Die Konsumentenrente bei p1 = 1 ist
kr(p1 ) = v(x1 ) − p1 x1 = 16 · 8 − 1 · 64 = 128 − 64 = 64.
Die Konsumentenrente bei p1 ∗ = 4 ist
kr(p∗1 ) = v(x∗1 ) − p∗1 x∗1 = 16 · 2 − 4 · 4 = 32 − 16 = 16.
Der Verlust an Konsumentenrente auf Grund der Preisänderung ist also 64 − 16 = 48.
10