Lösungen

Georg Nöldeke
Frühjahrssemester 2009
VWL 3: Mikroökonomie
Lösungshinweise zu Aufgabenblatt 1
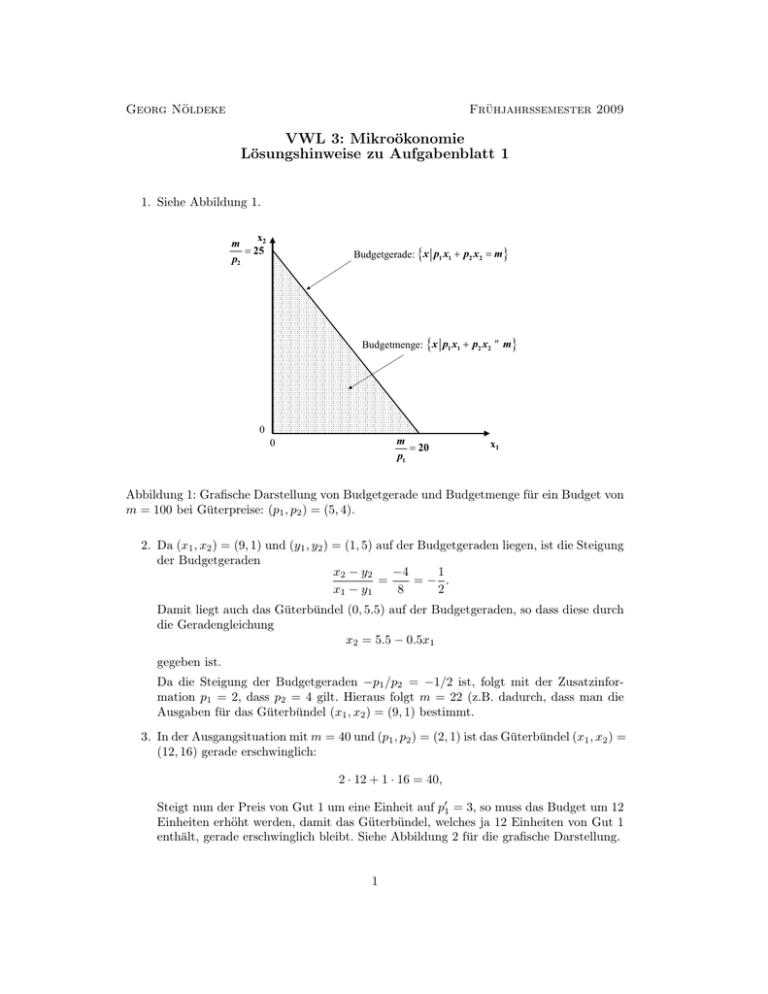
1. Siehe Abbildung 1.
x2
m
= 25
p2
Budgetgerade: {x p1 x1 + p2 x2 = m}
Budgetmenge: {x p1 x1 + p2 x2 ≤ m}
0
m
= 20
p1
0
x1
Abbildung 1: Grafische Darstellung von Budgetgerade und Budgetmenge für ein Budget von
m = 100 bei Güterpreise: (p1 , p2 ) = (5, 4).
2. Da (x1 , x2 ) = (9, 1) und (y1 , y2 ) = (1, 5) auf der Budgetgeraden liegen, ist die Steigung
der Budgetgeraden
−4
1
x2 − y2
=
=− .
x1 − y1
8
2
Damit liegt auch das Güterbündel (0, 5.5) auf der Budgetgeraden, so dass diese durch
die Geradengleichung
x2 = 5.5 − 0.5x1
gegeben ist.
Da die Steigung der Budgetgeraden −p1 /p2 = −1/2 ist, folgt mit der Zusatzinformation p1 = 2, dass p2 = 4 gilt. Hieraus folgt m = 22 (z.B. dadurch, dass man die
Ausgaben für das Güterbündel (x1 , x2 ) = (9, 1) bestimmt.
3. In der Ausgangsituation mit m = 40 und (p1 , p2 ) = (2, 1) ist das Güterbündel (x1 , x2 ) =
(12, 16) gerade erschwinglich:
2 · 12 + 1 · 16 = 40,
Steigt nun der Preis von Gut 1 um eine Einheit auf p01 = 3, so muss das Budget um 12
Einheiten erhöht werden, damit das Güterbündel, welches ja 12 Einheiten von Gut 1
enthält, gerade erschwinglich bleibt. Siehe Abbildung 2 für die grafische Darstellung.
1
x2
p1′ x1 + p2 x2 = 40
40
p1′ x1 + p2 x2 = 52
20
(12,16)
p1 x1 + p2 x2 = 40
0
0
20
40
x1
Abbildung 2: Die Ausgangsbudgetgerade hat die Achsenabschnitte (20, 0) und (0, 40). Nach
Anstieg des Preises p1 auf p01 = 3, dreht sich die Budgetgerade zum Ursprung um den vertikalen Achsenabschnitt, so dass der horizontale Achsenabschnitt durch (40/3, 0) gegeben ist.
Erhöht man nun das Budget um 12 Einheiten auf 52, so bedeutet dieses eine Parallelverschiebung der Budgetgeraden vom Ursprung weg. Die resultierende Budgetgerade verläuft
durch den Punkt (12, 16).
4. (a) Indifferenzkurven verlaufen streng fallend und streng konvex; Besserpfeile zeigen
nach rechts-oben. Siehe Abbildung 3.
(b) Indifferenzkurven verlaufen streng fallend; die Besserpfeile zeigen nach rechtoben. Die Indifferenzkurven verlaufen nicht streng konvex. Abbildung 4 zeigt
ein mögliches Beispiel.
(c) Eine Möglichkeit ist, einfach die Besserpfeile im Bild zu Teilaufgabe a) umzudrehen. Eine weitere Möglichkeit ist in Abbildung 5 dargestellt.
5. Ja, die Grafik kann eine Indifferenzkurve eine rationalen Präferenzrelation darstellen
- die Form der Indifferenzkurven ist im Prinzip beliebig.
Die Grafik kann allerdings nicht die Indifferenzkurve einer streng monotonen Präferenzrelation
darstellen: Bei einer monotonen Präferenzrelation muss das in Abbildung 6 grün markierten Güterbündel nämlich dem rot markierte Güterbündel streng vorgezogen werden
und kann daher nicht auf der gleichen Indifferenzkurve liegen.
6. Nein, die Präferenzrelation kann nicht artig sein. Wäre die Präferenzrelation artig, so
wäre sie streng konvex und streng monoton. Wegen strenger Konvexität müsste das
Güterbündel
1
1
x + y = (3, 3)
2
2
dem Güterbündel y (und auch x) streng vorgezogen werden. Aus strenger Monotonie der Präferenzrelation würde dann folgen, dass das Güterbündel z = (3, 4) dem
Güterbündel (3, 3) streng vorgezogen wird. Also müsste (Transitivität der Präferenzrelation)
z y gelten. Dieser Widerspruch zu der Annahme z ∼ y zeigt, dass die Präferenzrelation
nicht artig sein kann. Siehe Abbildung 7.
2
Abbildung 3: Indifferenzkurven und Besserpfeile zu einer streng konvexen und streng monotonen Präferenzrelation.
Abbildung 4: Indifferenzkurven und Besserpfeile zu einer streng monotonen, aber nicht konvexen Präferenzrelation.
7. Hinweis: Die Grenznutzen sind die partiellen Ableitungen der Nutzenfunktion. Um die
partielle Ableitung nach x1 zu bestimmen, betrachtet man x2 als Konstante und bildet
die Ableitung der resultierenden Funktion von x1 . Entsprechend bestimmt man die
partielle Ableitung nach x2 , indem man x1 als Konstante betrachtet und die Ableitung
der resultierenden Funktion von x2 bestimmt.
Zur Abkürzung der Schreibweise werden in den Antworten auf diese Aufgabe die Grenznutzen mit
∂u(x1 , x2 )
∂u(x1 , x2 )
u1 (x) :=
und u2 (x) :=
∂x1
∂x2
bezeichnet. Die Grenzrate der Substitution ist dann also jeweils durch
GRS(x) = −
u1 (x)
u2 (x)
gegeben.
(a) Die Grenznutzen sind
u1 (x) = a und u2 (x) = b.
Die Grenzrate der Substitution ist also
a
GRS(x) = − .
b
3
Abbildung 5: Indifferenzkurven und Besserpfeile zu einer Präferenzrelation, die weder konvex
noch monoton ist.
Abbildung 6: Die dargestellte Indifferenzkurve kann nicht zu einer monotonen
Präferenzrelation gehören.
(b) Die Grenznutzen sind
a
u1 (x) = √ und u2 (x) = 1.
x1
Die Grenzrate der Substitution ist also
a
GRS(x) = − √ .
x1
(c) Die Grenznutzen sind
u1 (x) = 4(x21 + x2 )x1 und u2 (x) = 2(x21 + x2 ).
Die Grenzrate der Substitution ist also
GRS(x) = −
4
4(x21 + x2 )x1
= −2x1 .
2(x21 + x2 )
Abbildung 7: Liegen (2, 5), (3, 4) und (4, 1) auf einer Indifferenzkurve, kann die
Präferenzrelation nicht artig sein.
(d) Die Grenznutzen sind
d
c d−1
u1 (x) = cxc−1
.
1 x2 und u2 (x) = dx1 x2
Die Grenzrate der Substitution ist also
GRS(x) = −
d
c x2
cxc−1
1 x2
=−
.
d−1
c
d x1
dx1 x2
(e) Die Grenznutzen sind
d
c
und u2 (x) =
.
x1
x2
u1 (x) =
Die Grenzrate der Substitution ist also
GRS(x) = −
c/x1
c x2
=−
.
d/x2
d x1
(f) Die Grenznutzen sind
u1 (x) = x2 − b und u2 (x) = x1 − a.
Die Grenzrate der Substitution ist also für x1 = a nicht definiert und ansonsten
durch
x2 − b
GRS(x) = −
x1 − a
gegeben.
(g) Die Grenznutzen sind
u1 (x) =
a
und u2 (x) = 1.
x1
Die Grenzrate der Substitution ist also
GRS(x) = −
5
a
.
x1
8. (a) Die Nutzenfunktionen in (b) und (g) sind quasilinear und stellen daher quasilineare Präferenzrelationen dar.
Obgleich die Nutzenfunktionen in (a) und (c) nicht quasilinear sind, stellen sie
ebenfalls quasilineare Präferenzrelationen dar. Die entscheidende Frage ist nämlich
nicht, ob die angegebenen Nutzenfunktionen quasilinear sind, sondern ob die
Präferenzrelationen durch eine solche Nutzenfunktion dargestellt werden können.
Dass dem so ist, kann man daran erkennen, dass die Grenzrate der Substitition
(oder - äquivalent - die marginale Zahlungsbereitschaft) nicht von x2 abhängt.
Konkret ist die quasilineare Nutzenfunktion
v(x1 , x2 ) =
a
x1 + x2
b
eine streng monotone Transformation der Nutzenfunktion in (a) und die quasilineare Nutzenfunktion
v(x1 , x2 ) = x21 + x2
eine streng monotone Transformation der Nutzenfunktion in (c).
Alle anderen betrachteten Nutzenfunktionen stellen keine quasilinearen Präferenzrelationen dar, da die Grenzrate der Substitution hier jeweils (auch) von x2
abhängt.
(b) Die Nutzenfunktion in (d) ist Cobb-Douglas und stellt damit auch eine CobbDouglas-Präferenzrelation dar. Die Nutzenfunktion in (e) ist zwar nicht CobbDouglas, ist aber eine streng monotone Transformation der Nutzenfunktion in
(d),
ln(xc1 xd2 ) = ln(xc1 ) + ln(xd2 ) = c ln x1 + d ln x2 ,
und stellt somit ebenfalls eine Cobb-Douglas-Präferenzrelation dar.
Alle anderen betrachteten Nutzenfunktionen stellen keine Cobb-Douglas-Präferenzrelation dar, da sich ihre Grenzraten der Substitution nicht in der Form GRS(x) =
−cx2 /(dx1 ) schreiben lassen.
(c) Die Nutzenfunktion in (f) kann keine artige Präferenzrelation darstellen, da sie
nicht monoton ist: z.B.ist der Grenznutzen des ersten Gutes für x2 < b streng
negativ. Für die anderen Nutzenfunktion gilt, dass die Grenznutzen streng positiv sind. Sie stellen also genau dann eine artige Präferenzrelationen dar, wenn
die marginale Zahlungsbereitschaft entlang einer jeden Niveaulinie der Nutzenfunktion (das ist eine Indifferenzkurve der dargestellten Präferenzrelation) streng
fallend ist (bzw. die Grenzrate der Substitution streng steigend ist).
Die Nutzenfunktion in (a) stellt perfekte Substitute da; ihre Niveaulinien sind
Geraden und besitzen somit konstante Steigung. Sie stellt damit keine artige
Präferenzrelation dar.
Die quaslineare Nutzenfunktion in (b) stellt eine artige Präferenzrelation dar, da
−1/2
die marginale Zahlungsbereitschaft ax1
streng fallend in x1 ist:
−1/2
∂ax1
∂x1
a −3/2
< 0.
= − x1
2
Da die marginale Zahlungsbereitschaft nicht von x2 abhängt, sichert dieses, dass
jede Indifferenzkurve streng konvex verläuft.
6
Aus dem gleichen Grunde ist auch die Präferenzrelation, die durch die Nutzenfunktion in (g) dargestellt wird, artig:
∂ax−1
1
= −ax−2
1 < 0.
∂x1
Siehe Abbildungen 8 und 9.
Abbildung 8: Niveaulinien der Nutzenfunktion u(x1 , x2 ) =
√
x1 + x2 .
Die Nutzenfunktion in (c) stellt keine artige Präferenzrelation dar, da die marginale Zahlungsbereitschaft 2x1 streng steigend in x1 ist. Siehe Abbildung 10.
Die marginale Zahlungsbereitschaft (cx2 )/(dx1 ) der Nutzenfunktionen in (d) und
(e) ist streng fallend in x1 und streng steigend in x2 . Da bei einer Bewegung
entlang einer Indifferenzkurve eine Erhöhung von x1 mit einer Absenkung von
x2 einhergeht, ist die marginale Zahlungsbereitschaft entlang einer jeden Indifferenzkurve streng fallend. Die Nutzenfunktionen in (d) und (e) stellen also eine
artige Präferenzrelation dar.
9. Die Nutzenfunktion
√
u(x1 , x2 ) = 4 x1 + x2
√
ist quasilinear : u(x1 , x2 ) = v(x1 ) + x2 , wobei v(x1 ) = 4 x1 . Da die Funktion v streng
1
steigend und streng konkav ist,
2
−3
v 0 (x1 ) = √ > 0, v 00 (x1 ) = −x1 2 < 0,
x1
ist die Nutzenfunktion zudem artig. Es gibt also eine eindeutige Lösung des Konsumentenproblems.
1 Diese Berechnung ist eigentlich überflüssig, da es sich hier um einen Spezialfall der Nutzenfunktion aus
Aufgabe 7(b) handelt. Siehe auch die Antwort auf Aufgabe 8(c).
7
Abbildung 9: Niveaulinien der Nutzenfunktion u(x1 , x2 ) = ln(x1 ) + x2 .
(a) Gibt es ein Güterbündel x∗ , welches die Bedingung erster Ordnung
p1
u1 (x∗ )
=
u2 (x∗ )
p2
erfüllt2 und auf der Budgetgeraden liegt,
p1 x∗1 + p2 x∗2 = m,
so ist es bei einer artigen Präferenzrelation optimal. Wir versuchen also ein solches
Güterbündel zu finden:
Da p2 = 1 gilt, besagt die Bedingung erster Ordnung, dass die marginale Zahlungsbereitschaft für Gut 1 mit dem Preis von Gut 1 übereinstimmt:
2
1
p ∗ = ⇔ x∗1 = 16.
2
x1
Damit ein Bündel mit x∗1 = 16 auf der Budgetgeraden liegt, muss
1
x∗2 = m − p1 x∗1 = 10 − 16 = 2.
2
gelten. Die Lösung des Konsumentenproblems ist also x∗ = (16, 2). Siehe Abbildung 11.
(b) Mit p1 = 1/4 folgt aus der Bedingung erster Ordnung
2
1
p ∗ = ,
4
x1
2 Siehe
den Lösungshinweis zu Aufgabe 7 für die verwendete Notation.
8
Abbildung 10: Niveaulinien der Nutzenfunktion u(x1 , x2 ) = (x21 + x2 )2 .
so dass x∗1 = 64 in einem Güterbündel gilt, welches die Bedingung erster Ordnung
erfüllt. Die Ausgaben für Gut 1 wären dann aber p1 x∗1 = 16 und würden somit
das Budget von m = 10 übersteigen.
Also muss es sich bei der Lösung des Konsumentenproblems um eine Randlösung
handeln, in der die Konsumentin ihr gesamtes Budget für Gut 1 ausgibt. Also
gilt:
m
x∗1 =
= 40, x∗2 = 0.
p1
Siehe Abbildung 12.
10. Es handelt sich um perfekte Substitute, bei denen die marginale Zahlungsbereitschaft
für Gut 1 durch a = 1/4 gegeben ist (Vgl. Aufgabe 7(a)).
(a) Da der relative Preis 5/24 hier streng kleiner als die marginale Zahlungs bereitschaft 1/4 ist, wird der Konsument sein gesamtes Budget für Gut 1 ausgeben.
Das optimale Güterbündel ist also (24, 0).
(b) Der relative Preis steigt nun auf 5/15 = 1/3 > 1/4. Da der relative Preis streng
oberhalb der marginalen Zahlungsbereitschaft liegt, ist es optimal, das gesamte
Budget für Gut 2 auszugeben. Das optimale Güterbündel ist also (0, 8).
(c) Siehe Abbildung 13.
11. Die Budgetidentität ist hier erfüllt:
p1 f1 (p1 , p2 , m) + p2 f2 (p1 , p2 , m) = (m − p2 + 1) + (p2 − 1) = m.
Die Nachfragefunktion ist nicht homogen vom Grad Null in Preisen und Budget. Insbesondere gilt für t 6= 1:
f2 (tp1 , tp2 , tm) = 1 −
1
1
6= f2 (p1 , p2 , m) = 1 − .
tp2
p2
9
Abbildung 11: Die Lösung des Konsumentenproblems zu Aufgabe 12(a).
Anmerkung: Die Einschränkung des Definitionsbereichs auf m + 1 > p2 > 1 in der
Aufgabenstellung sichert, dass die nachgefragten Güterbündel im Güterraum liegen:
m + 1 − p2 > 0 impliziert
f1 (p1 , p2 , m) =
m + 1 − p2
> 0,
p2
während p2 − 1 > 0 sichert, dass
f2 (p1 , p2 , m) =
p2 − 1
>0
p2
gilt. Es werden also in allen betrachteten Situationen streng positive Mengen beider
Güter konsumiert.
12. Das beschriebene Nachfrageverhalten verletzt das schwache Axiom der offenbarten
Präferenzen. Um dieses zu sehen, bemerke man, dass
x̃1 p1 + x̃2 p2 = 95 < m = 100,
d.h. das Güterbündel (x̃1 , x̃2 ) ist erschwinglich, wenn (x1 , x2 ) nachgefragt wird. Zugleich gilt aber auch:
x1 p̃1 + x2 p̃2 = 112 < m̃ = 116,
d.h. das Güterbündel (x1 , x2 ) ist erschwinglich, wenn (x̃1 , x̃2 ) nachgefragt wird. Da
(x1 , x2 ) 6= (x̃1 , x̃2 ) gilt, ist das schwache Axiom damit verletzt.
13. Die gesuchte Engelkurve ist durch die Funktion g1 : R++ → R+ gegeben, welche durch
g1 (m) = f1 (1, 1, m)
definiert ist. In Worten: Bei den gegebenen Preisen (p1 , p2 ) = (1, 1) für die beiden Güter
wird jedem Einkommen m die Menge von Gut 1 zugeordnet, die bei Einkommen m
nachgefragt wird.
10
Abbildung 12: Die Lösung des Konsumentenproblems zu Aufgabe 12(b).
Die gesuchte Nachfragekurve ist durch die Funktion d1 : R++ → R+ gegeben, welche
durch
d1 (p1 ) = f1 (p1 , 1, 10)
definiert ist. In Worten: Bei gegebenem Preis p2 = 1 und Einkommen m = 10 wird
jedem Preis p1 die Menge von Gut 1 zugeordnet, die bei Preis p1 nachgefragt wird.
(a) Hier ist das optimale Güterbündel x∗ bei gegebenen Preisen (p1 , p2 ) und Einkommen m eindeutig als die Lösung der Gleichungen
ax∗1 = x∗2 und p1 x∗1 + p2 x∗2 = m
bestimmt. Die dazugehörige Nachfragefunktion ist somit durch
f1 (p1 , p2 , m) =
m
am
, f2 (p1 , p2 , m) =
p1 + ap2
p1 + ap2
gegeben.
Die gesuchte Engelkurve ist also
g1 (m) =
m
.
1+a
d1 (p1 ) =
10
.
p1 + a
Die gesuchte Nachfragekurve ist
(b) Hier ist das optimale Güterbündel x∗ bei gegebenen Preisen (p1 , p2 ) und Einkommen m eindeutig als die Lösung der Gleichungen
p1
ax∗2
=
und p1 x∗1 + p2 x∗2 = m
(1 − a)x∗1
p2
bestimmt. Die dazugehörige Nachfragefunktion ist somit durch
f1 (p1 , p2 , m) = a
m
m
und f2 (p1 , p2 , m) = (1 − a)
p1
p2
11
Abbildung 13: Die optimalen Güterbündel zu Aufgaben 13(a) und (b).
gegeben.
Die gesuchte Engelkurve ist also
g1 (m) = am.
Die gesuchte Nachfragekurve ist
d1 (p1 ) = a
10
.
p1
(c) Haben die Gleichungen
p1
1
=
und p1 x∗1 + p2 x∗2 = m
∗
x1
p2
eine Lösung mit x∗1 ≥ 0 und x∗2 ≥ 0, so ist x∗ das eindeutige optimale Güterbündel
bei gegebenen Preisen (p1 , p2 ) und Einkommen m. Löst man die Gleichungen, so
erhält man
p2
m
x∗1 =
und x∗2 =
− 1.
p1
p2
Für m ≥ p2 ist die Nachfragefunktion also durch
f1 (p1 , p2 , m) =
p2
m
und f2 (p1 , p2 , m) =
−1
p1
p2
gegeben. Für m < p2 liegt eine Randlösung des Konsumentenproblems vor; die
Nachfragefunktion ist hier durch
f1 (p1 , p2 , m) =
m
und f2 (p1 , p2 , m) = 0
p1
gegeben.
Die gesuchte Engelkurve ist also
g1 (m) = min{m, 1}.
12
Die gesuchte Nachfragekurve ist
d1 (p1 ) =
1
.
p1
14. (a) Siehe Abbildung 14.
Abbildung 14: Ist Gut 1 inferior, so fällt die nachgefragte Menge mit steigendem Einkommen.
Gilt die Budgetidentität, so muss gleichzeitig die nachgefragte Menge von Gut 2 steigen,
so dass die Einkommens-Konsumkurve eine negative Steigung besitzt, deren Absolutwert
grösser als der Absolutwert der Steigung der Budgetgeraden ist.
Beachten Sie die folgenden allgemeinen Punkte zur Darstellung von EinkommensKonsumkurven:
• Eine Einkommens-Konsumkurve muss vom Ursprung des Koordinatensystems ausgehen: Kein Einkommen impliziert keinen Konsum.
• Eine Bewegung entlang der Kurve, die vom Ursprung wegführt, beschreibt
die Auswirkung einer Einkommenserhöhung.
• Gilt die Budgetidentität, so kann die Einkommens-Konsumkurve jede Budgetgerade nur einmal schneiden.
(b) Siehe Abbildung 15.
Beachten Sie die folgenden allgemeinen Punkte zur Darstellung von Preis-Konsumkurven bei Veränderung des Preis von Gut 1:
• Die Preis-Konsumkurve läuft auf einen Punkt auf der vertikalen Achse zu:
Geht der Preis von Gut 1 gegen unendlich, so geht die nachgefragte Menge
von Gut 1 gegen Null, während die nachgefragte Menge von Gut 2 nicht
grösser als m/p2 werden kann.
• Eine Bewegung entlang der Kurve, welche auf die vertikale Achse zuführt,
beschreibt die Auswirkung einer Preiserhöhung.
• Gilt die Budgetidentität, so kann die Preis-Konsumkurve jede Budgetgerade
nur einmal schneiden. Ist Gut 1 gewöhnlich, so ist im Schnittpunkt mit einer
Budgetgeraden die Steigung der Preis-Konsumkurve grösser als die Steigung
der Budgetgeraden - die Kurve verläuft also flacher.
13
Abbildung 15: Ist Gut 2 ein Komplement für Gut 1, so fällt die nachgefragte Menge von
Gut 2 mit steigendem Preis von Gut 1. Ist zugleich Gut 1 gewöhnlich, so bedeutet dies, dass
die Preis-Konsumkurve von Gut 1 steigend verläuft. Ist Gut 2 ein Substitut für Gut 1 und
Gut 1 gewöhnlich, so verläuft die Preis-Konsumkurve fallend.
(c) Siehe Abbildung 16.
15. (a) Die erforderliche Einkommenskompensation ist durch
∆m = ∆p1 x1 + ∆p2 x2 = 1 · 10 + 3 · 5 = 25
gegeben.
Anmerkung: Man könnte auch wie folgt argumentieren. In der Ausgangssituation sind die Ausgaben für das Bündel (x1 , x2 ) = (10, 5) (und damit das Budget
des Konsumenten) gleich 65. In der neuen Situation sind die Ausgaben für dieses
Bündel 90. Also muss das Budget des Konsumenten um 25 erhöht werden, damit
das Bündel gerade erschwinglich bleibt.
(b) Der relative Preis von Gut 1 fällt hier von p1 /p2 = 5/3 auf p01 /p02 = 6/6 = 1
(die Budgetgerade wird also flacher), so dass der Substitutionseffekt identisch
zu dem Effekt einer Reduktion des Preises von Gut 1 bei unverändertem Preis
von Gut 2 ist. Der Substitionseffekt auf Gut 1 ist also positiv, ∆xS1 ≥ 0, der
Substitutionseffekt auf Gut 2 ist negativ; ∆xS2 ≤ 0. Siehe Abbildung 17.
(c) Ist Gut 1 normal, so ist der Einkommenseffekt auf Gut 1 hier negativ, da
auf Grund der Preisänderung die Kaufkraft des Konsumenten gefallen ist. Da
der Substitutionseffekt auf Gut 1 positiv war, lässt sich über den Gesamteffekt in diesem Falle nichts aussagen. Ist hingegen Gut 1 inferior, so ist der
Einkommenseffekt auf die nachgefragte Menge von Gut 1 positiv, so dass der
Gesamteffekt sicherlich positiv ist.
Anmerkung: Betrachten Sie noch einmal Abbildung 17, um das folgende zu
sehen.
• Selbst wenn der Konsument sein gesamtes Einkommen von 65 für Gut 1
ausgibt, kann er sich in der neuen Situation nur 65/6 Einheiten dieses Gutes
14
Abbildung 16: Ist Gut 1 Giffen, so steigt die nachgefragte Menge des Gutes mit steigendem
Preis p1 . Gilt die Budgetidentität, so muss die nachgefragte Menge von Gut 2 dann fallen.
Ist Gut 1 ein Giffen-Gut, so verläuft die Preis-Konsumkurve also fallend. Im Unterschied zu
der Situation, in der Gut 1 gewöhnlich und Gut 2 ein Substitut für Gut 1 ist, verläuft sie
dabei steiler als die Budgetgeraden, welche sie schneidet.
leisten. Ist der Substitutionseffekt ∆xS1 ≥ 5/6, so ist es also ausgeschlossen,
dass Gut 1 in Bezug auf die zu betrachtende Einkommensänderung inferior
ist.
• Wäre in der Aufgabenstellung die neue Situation durch (p01 , p02 ) = (7, 7) gegeben gewesen, so wäre in der neuen Situation ein Güterbündel mit x01 ≥ 10
nicht erschwinglich. Ohne irgendwelche Überlegungen zu Substitutions- und
Einkommenseffekten folgt in diesem Fall also, dass der Gesamteffekt auf Gut
1 negativ sein muss.
16. (a) Anmerkung: Es handelt sich um die Nachfragefunktion eines Konsumenten mit
Cobb-Douglas-Präferenzrelation.
Steigt der Preis von Gut 1 um ∆p1 , so ist der Gesamteffekt auf die Nachfrage der
beiden Güter
1
1
∆x1 = f1 (p1 + ∆p1 , p2 , m) − f1 (p1 , p2 , m) = c m
−
p1 + ∆p1
p1
∆x2 = f2 (p1 + ∆p1 , p2 , m) − f2 (p1 , p2 , m) = 0.
Um den Substitutions- und den Einkommenseffekt zu berechnen, muss man die
erforderliche Einkommenskompensation bestimmen. Damit sich der Konsument
nach der Preisänderung immer noch das ursprünglich gewählte Güterbündel leisten kann, muss
c m ∆p1
∆m = ∆p1 f1 (p1 , p2 , m) =
(1)
p1
15
Abbildung 17: Die rote Budgetgerade stellt die Ausgangssituation dar, die blaue Budgetgerade die neue Situation, die pinke Budgetgerade die einkommenskompensierte Situation. Die eingezeichnete Indifferenzkurve durch das in der Ausgangssituation nachgefragte
Güterbündel verdeutlicht, dass der Substitutionseffekt für das erste Gut positiv sein muss.
gelten. Der Substitutionseffekt auf die Nachfrage der beiden Güter ist
1 + ∆m/m
1
−
p1 + ∆p1
p1
∆xS
1 =
f1 (p1 + ∆p1 , p2 , m + ∆m) − f1 (p1 , p2 , m) =
cm
∆xS
2 =
f2 (p1 + ∆p1 , p2 , m + ∆m) − f2 (p1 , p2 , m) =
1−c
∆m.
p2
Setzt man für ∆m aus (1) ein, so erhält man:
∆xS1 = −
c m (1 − c)
c m (1 − c)
∆p1 , ∆xS2 =
∆p1 .
p1 (p1 + ∆p1 )
p1 p2
Insbesondere sieht man, dass für ∆p1 > 0 der Substitutionseffekt auf die Nachfrage von Gut 1 negativ ist, während der Substitutionseffekt auf die Nachfrage
von Gut 2 positiv ist, da
−
c m (1 − c)
c m (1 − c)
< 0 und
>0
p1 (p1 + ∆p1 )
p1 p2
gilt.
Der Einkommenseffekt bestimmt sich als
∆xI1 =
f1 (p1 + ∆p1 , p2 , m) − f1 (p1 + ∆p1 , p2 , m + ∆m) =
∆xI2 =
f2 (p1 + ∆p1 , p2 , m) − f2 (p1 + ∆p1 , p2 , m + ∆m) =
16
c ∆m
p1 + ∆p1
(1 − c) ∆m
−
p2
−
Setzt man für ∆m aus (1) ein, so erhält man
c2 m
∆p1
p1 (p1 + ∆p1 )
(1 − c) c m
∆xI2 = −
∆p1 .
p1 p2
∆xI1 = −
Insbesondere ist der Einkommenseffekt auf die Nachfrage beider Güter negativ:
Im Fall von Gut 1 verstärkt der Einkommenseffekt den Substitutionseffekt; im
Fall von Gut 2 hebt er ihn gerade auf.
Abbildung 18 verdeutlicht diese Ergebnisse.
Abbildung 18: Die rote Budgetgerade stellt die Ausgangssituation dar, die blaue Budgetgerade die neue Situation, die pinke Budgetgerade die einkommenskompensierte Situation.
Der Substitutionseffekt entspricht der Bewegung von dem roten Güterbündel zu dem pinken Güterbündel. Der Einkommenseffekt entspricht der Bewegung von dem pinken zu dem
blauen Güterbündel. Für Gut 2 wird der positive Substitutionseffekt durch den negativen Einkommenseffekt gerade aufgehoben. (Die Abbildung wurde für die Cobb-Douglas0.5
Nutzenfunktion u(x1 , x2 ) = x0.5
1 x2 erstellt.)
(b) Anmerkung: Es handelt sich um die Nachfragefunktion eines Konsumenten, für
den die Güter perfekte Komplemente sind. Vergleichen Sie mit Abbildung 8.4 des
Lehrbuches.
Der Gesamteffekt bestimmt sich nun als
1
1
∆x1 = m
−
,
p1 + ∆p1 + ap2
p1 + ap2
1
1
∆x2 = am
−
.
p1 + ∆p1 + ap2
p1 + ap2
17
Die erforderliche Einkommenskompensation berechnet sich als
∆m =
m
∆p1 .
p1 + ap2
Der Substitutionseffekt ist
∆xS1
∆xS2
m + ∆m
m
−
,
p1 + ∆p1 + ap2
p1 + ap2
m + ∆m
m
= a
−
.
p1 + ∆p1 + ap2
p1 + ap2
=
Setzt man für ∆m ein, so erhält man
∆xS1 =
m
p +ap2
∆xS2 = a
1
−
m
p1 +ap2
m
p1 +ap2
−
m
p1 +ap2
=0
= 0.
Der Substitutionseffekt ist also im Fall perfekter Komplemente gleich Null. Damit
erübrigen sich auch weitere Berechnungen zur Bestimmung des Einkommenseffekts: Es gilt
∆xI1 = ∆x1 , ∆xI2 = ∆x2 .
(c) Anmerkung: Es handelt sich um die Nachfragefunktion eines Konsumenten mit
quasilinearer Präferenzordnung, die durch
u(x1 , x2 ) = ln x1 + x2
dargestellt wird. Vergleichen Sie mit Abbildung 8.6 im Lehrbuch, welche Substitutionsund Einkommenseffekte für den Fall einer (anderen) quasilinearen Präferenzrelation
darstellt.
Der Gesamteffekt bestimmt sich nun als
p2
p2
∆x1 =
− ,
p1 + ∆p1
p1
∆x2 = 0.
Die erforderliche Einkommenskompensation berechnet sich als
∆m =
p2
∆p1 .
p1
Der Substitutionseffekt ist
∆xS1
=
∆xS2
=
p2
p2
− ,
p1 + ∆p1
p1
∆m
∆p1
=
.
p2
p1
Da ∆xS1 = ∆x1 , ist der Einkommenseffekt auf Gut 1 gleich Null. Da ∆x2 = 0,
ist der Einkommenseffekt auf Gut 2 durch ∆xI2 = −∆xS2 gegeben. Also:
∆xI1
=
0,
∆xI2
=
−
Hinweise:
18
∆p1
.
p1
• Vorausgesetzt, dass sowohl in der Ausgangssituation als auch in der neuen
Situation eine streng positive Menge von Gut 1 nachgefragt wird, ist der Einkommenseffekt auf Gut 1 im Fall quasilinearer Präferenzrelationen allgemein
gleich Null, da die nachgefragte Menge von Gut 1 nicht vom Einkommen
abhängt.
• Hingegen ist es im allgemeinen nicht der Fall, dass sich kein Gesamteffekt
auf Gut 2 ergibt. Dieses liegt an der speziellen Form der hier betrachteten
Nachfragefunktion, in der die Ausgaben des Konsumenten für Gut 2 nicht
von dem Preis von Gut 1 abhängen.
17. (a) Besitzen die beiden Konsumenten identische Cobb-Douglas-Präferenzrelationen,
welche durch die Nutzenfunktion
u(x1 , x2 ) = xc1 x1−c
2
dargestellt werden, so gilt für ihrer Nachfragefunktionen
f1a (p1 , p2 , ma ) = c
ma
ma
, f2a (p1 , p2 , ma ) = (1 − c)
.
p1
p2
Die Marktnachfragefunktion für Gut 1 ist also
F1 (p1 , p2 , m1 , m2 ) = c
m1
m2
M
+c
=c ,
p1
p1
p1
und entsprechend für Gut 2:
F2 (p1 , p2 , m1 , m2 ) = (1 − c)
m1
m2
M
+ (1 − c)
= (1 − c) .
p1
p1
p1
Hinweis: Die Präferenzrelation des repräsentativen Konsumenten stimmt in diesem Falle also mit der Präferenzrelation der betrachteten Konsumenten überein.
Für andere (homothetische und identische) Präferenzrelationen muss das nicht so
sein.
(b) Werden die Präferenzen der Konsumenten durch die Nutzenfunktionen
1−α
u1 (x1 , x2 ) = xα
1 x2
und
u2 (x1 , x2 ) = xβ1 x1−β
2
mit α 6= β dargestellt, so ist die Marktnachfragefunktion von Gut 1
F1 (p1 , p2 , m1 , m2 ) = α
m2
M
m2
m1
+β
=α
+ (β − α)
.
p1
p1
p1
p1
Hält man also das aggregierte Einkommen konstant, ändert aber m2 , so ändert
sich die Marktnachfrage, da β − α 6= 0 gilt.
Hinweis: Auch ohne die geforderten Berechnungen sollte klar sein, was das Problem ist: Besitzen die Engelkurven der Konsumenten für ein Gut unterschiedliche
Steigungen, so führt eine Umverteilung von Einkommen zu einer Änderung der
nachgefragten Menge.
19
(c) Die Engelkurve von Gut 1 für einen Konsumenten mit der angegebenen Nutzenfunktion bei p1 = p2 = 1 ist durch
g(m) = f (1, 1, m) = min{m, 100}
gegeben.3 Für die Marktnachfragefunktion gilt also
F1 (1, 1, m1 , m2 ) = min{m1 , 100} + min{m2 , 100}.
Betrachtet man nun eine Situation mit m1 = 110, m2 = 90, so werden insgesamt
190 Einheiten von Gut 1 nachgefragt. Nimmt man Konsument 2 eine Einheit Einkommen weg und gibt sie Konsument 1, so ist die Marktnachfrage anschliessend
nur noch 189, obgleich nach wie vor M = 200 gilt.
3 Wieso? Da die Nutzenfunktion quasilinear ist, ist die Bedingung erster Ordnung, welche die nachgefragte
Menge von Gut 1 bestimmt, durch
10
p1
=
√
x1
p2
gegeben. Mit p1 = p2 = 1 wird diese Bedingung durch x1 = 100 gelöst. Gilt m < 100, so tritt eine
Randlösung auf, in welcher der Konsument sein gesamtes Budget für Gut 1 ausgibt.
20