statistik1-ue-klausur1997

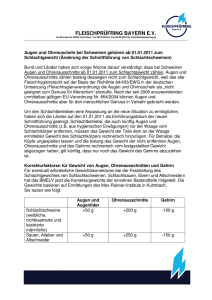
Übungsklausur Statistik 1 von 1997
Diese Klausur wurde heruntergeladen von www.informatiker.at.tf
1) Bei der Erhebung des Alters der aktiven Mitglieder eines Turnvereines erhält man folgendes
Ergebnis
Alter (gerundet auf Jahre)
Anzahl der Mitglieder
18
15
19
18
20
37
21
39
22
20
23
18
24
15
25
6
26
2
Um welche Art von Merkmalen handelt es sich hierbei?
Berechnen Sie
a) den Median
b) jenes Alter, das nur von 25% der Mitglieder überschritten wird
c) Zeichnen Sie die Verteilungsfunktion und überprüfen Sie graphisch die Ergebnisse aus a) und
b)
2) Eine stetige Zufallsvariable besitzt die Dichtefunktion
ke3 x für x  0
f ( x)  
0 sonst

a) Bestimmen sie k.
b) Bestimmen Sie die Wahrscheinlichkeit für X.
c) Wie groß ist die Wahrscheinlichkeit für P(0.5X1)
3) In einer Unfallambulanz eines Krankenhaus werden im Durchschnitt 3 Notfallpatienten pro
Stunde eingeliefert. Wie groß ist die Wahrscheinlichkeit, daß
a) in einer Stunde höchstens 2 Patienten eingeliefert werden
b) in drei Stunden insgesamt genau 6 Patienten eingeliefert werden
c) in drei Stunden jeweils genau 2 Patienten pro Stunde eingeliefert werden.
4) Man weiß, daß 55% der Bevölkerung einer Stadt mit 12000 Einwohnern Frauen sind. Für eine
Befragung soll eine Stichprobe von 100 Personen ausgewählt werden. Wie groß ist die
Wahrscheinlichkeit, daß in der Stichprobe mehr als 65 Frauen sind?
a) Exakte Lösung (Ansatz genügt)
b) Mittels Approximation
5) Das Schlachtgewicht von Schweinen (eines bestimmten Alters) aus der Aufzucht eines
biologischen Betriebes ist normalverteilt mit Mittelwert 100kg und einer Varianz von 400kg2.
a) Berechnen Sie die Wahrscheinlichkeit für folgendes Ereignis:
Schlachtgewicht größer als 120kg oder kleiner als 95kg
b) Die Wahrscheinlichkeit, daß ein Schwein das Mindestgewicht nicht erreicht, ist 5%. Wie groß
ist das Mindestgewicht?
c) Wie groß ist die Wahrscheinlichkeit, daß die Gewichtsdifferenz von 2 zufällig ausgewählten
Schweinen größer als 20kg ist?
d) Bei einer Anlieferung von 10 Schweinen werden folgende Schlachtgewichte bestimmt.
137
92
111
110
126
86
76
113
114
92
Kann die Behauptung aufrecht erhalten werden, daß diese Schweine aus biologischen Betrieb
stammen?
Bestimmen Sie zur Beantwortung dieser Frage ein symmetrisches Konfidenzintervall für den
Mittelwert der Variablen X = Schlachtgewicht eines Schweins jener Aufzuchtsart, aus der
diese Anlieferung stammt (Normalverteilung wird vorausgesetzt =0.95).