Einsatz des graphikfähigen TR in der Sek I
Werbung
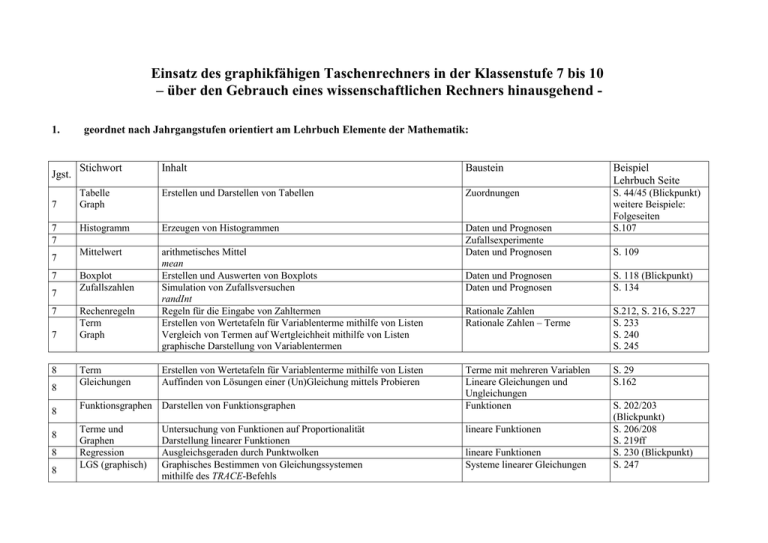
Einsatz des graphikfähigen Taschenrechners in der Klassenstufe 7 bis 10 – über den Gebrauch eines wissenschaftlichen Rechners hinausgehend 1. Jgst. 7 7 7 7 7 7 7 7 8 8 8 8 8 8 geordnet nach Jahrgangstufen orientiert am Lehrbuch Elemente der Mathematik: Stichwort Inhalt Baustein Beispiel Lehrbuch Seite Tabelle Graph Erstellen und Darstellen von Tabellen Zuordnungen Histogramm Erzeugen von Histogrammen Mittelwert arithmetisches Mittel mean Erstellen und Auswerten von Boxplots Simulation von Zufallsversuchen randInt Regeln für die Eingabe von Zahltermen Erstellen von Wertetafeln für Variablenterme mithilfe von Listen Vergleich von Termen auf Wertgleichheit mithilfe von Listen graphische Darstellung von Variablentermen Daten und Prognosen Zufallsexperimente Daten und Prognosen S. 44/45 (Blickpunkt) weitere Beispiele: Folgeseiten S.107 Boxplot Zufallszahlen Rechenregeln Term Graph Term Gleichungen Erstellen von Wertetafeln für Variablenterme mithilfe von Listen Auffinden von Lösungen einer (Un)Gleichung mittels Probieren Funktionsgraphen Darstellen von Funktionsgraphen Terme und Graphen Regression LGS (graphisch) Untersuchung von Funktionen auf Proportionalität Darstellung linearer Funktionen Ausgleichsgeraden durch Punktwolken Graphisches Bestimmen von Gleichungssystemen mithilfe des TRACE-Befehls S. 109 Daten und Prognosen Daten und Prognosen S. 118 (Blickpunkt) S. 134 Rationale Zahlen Rationale Zahlen – Terme S.212, S. 216, S.227 S. 233 S. 240 S. 245 Terme mit mehreren Variablen Lineare Gleichungen und Ungleichungen Funktionen S. 29 S.162 lineare Funktionen lineare Funktionen Systeme linearer Gleichungen S. 202/203 (Blickpunkt) S. 206/208 S. 219ff S. 230 (Blickpunkt) S. 247 Term Graph 9 9 Regression Gleichungen 10 10 10 10 10 10 10 10 10 Iteration Rekursion Tern Graph Regression Binomialverteilungen Graphische Darstellung quadratischer Funktionen Quadratfunktionen - Parabeln Abbildungen der Normalparabel Scheitelpunktsform graphisches Lösungsverfahren quadratischer Gleichungen Nullstellenbestimmung mithilfe des ZERO-Befehls im Menü CALCULATE Scheitelpunktsbestimmung mithilfe des Befehls MINIMUM/MAXIMUM im Menü CALCULATE Quadratische Regression Quadratische Funktionen S. 203 Lösen von Gleichungen mithilfe von Graph, Tabelle und Rechner Befehl aus dem CALCULATE-Menü: intersect Befehl aus dem MATH-Menü: solver Iterationsverfahren zur Bestimmung von Nullstellen Erstellen und Darstellen von rekursiven Formeln Überlagerung von linearen und exponentiellen Prozessen Darstellung von Potenzfunktionen Gleichungslöseverfahren S. 8 ff Gleichungslöseverfahren Wachstumsprozesse S. 43 S. 95 S. 146 S. 127 Nichtlineare Regression Bestimmung von Erfolgsw’keiten für k Erfolge bei n-stufigem BERNOULLI-Versuch mithilfe von binompdf(n,p,k) im Menü DISTR Bestimmen von kumulierten W’keiten mithilfe von binomcdf(n,p,k) im Menü DISTR Histogramme für Binomialverteilungen Trigonometrische Fkt. Darstellung von Graphen trigonometrischer Funktionen Untersuchung funktionaler Zusammenhänge SinRegression Modellieren mithilfe einer Sinusfunktion Parameterdarstellung Darstellung eines Kreises Wachstumsprozesse Wachstumsprozesse Bernoulli-Ketten und AlternativTests S. 208/209, S. 223 S. 211 S. 241 S.244/245 (Blickpunkt) S. 141 (Blickpunkt) S. 224 S. 229 Modellieren periodischer Vorgänge Modellieren periodischer Vorgänge Modellieren periodischer Vorgänge S.253 f.f S. 262/265 S. 268 S. 272 2. Funktionsweisen des Taschenrechners, die den Schülerinnen und Schülern nach der Klassenstufe 10 bekannt sein müssen: 1. sämtliche Tasten innerhalb des Display- Bereiches: Y=/STAT PLOT, WINDOW/TBLSET, ZOOM/FORMAT, TRACE/CALC, GRAPH/TABLE 2. die Taste STAT zur Erstellung von Tabellen 3. die Taste MATH mit der Funktion SOLVER zum Lösen von Gleichungen 4. die Taste DISTR mit der Funktion BINOMCDF und BINOMPDF innerhalb der Unterrichtseinheit Binomialverteilung