Theorie Potenzfunktionen

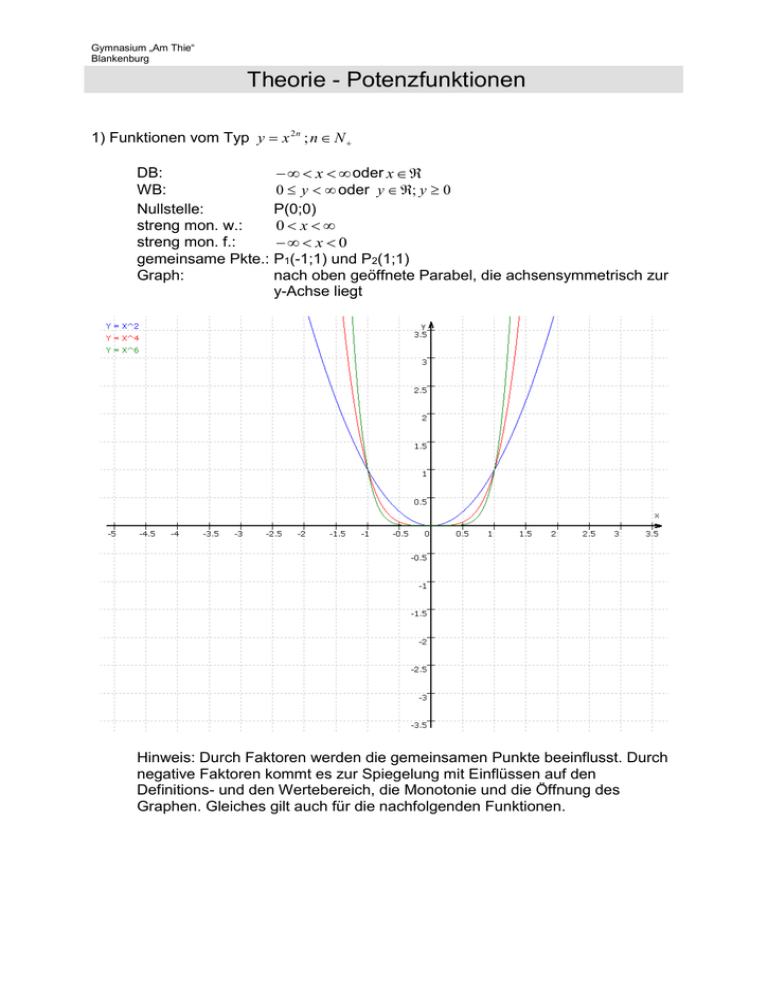
Gymnasium „Am Thie“
Blankenburg
Theorie - Potenzfunktionen
1) Funktionen vom Typ y  x 2 n ; n  N 
DB:
   x   oder x  
0  y   oder y  ; y  0
WB:
Nullstelle:
P(0;0)
streng mon. w.:
0 x
streng mon. f.:
  x  0
gemeinsame Pkte.: P1(-1;1) und P2(1;1)
Graph:
nach oben geöffnete Parabel, die achsensymmetrisch zur
y-Achse liegt
Hinweis: Durch Faktoren werden die gemeinsamen Punkte beeinflusst. Durch
negative Faktoren kommt es zur Spiegelung mit Einflüssen auf den
Definitions- und den Wertebereich, die Monotonie und die Öffnung des
Graphen. Gleiches gilt auch für die nachfolgenden Funktionen.
Gymnasium „Am Thie“
Blankenburg
Theorie - Potenzfunktionen
2) Funktionen vom Typ y  x 2 n1 ; n  N 
DB:
x 
y 
WB:
Nullstelle:
P(0;0)
streng mon. w.:
  x  
streng mon. f.:
nie
gemeinsame Pkte.: P1(-1;-1) und P2(1;1)
Graph:
Parabeln 3., 5....Grades, die punktsymmetrisch zum
Koordinatenursprung liegen
Gymnasium „Am Thie“
Blankenburg
Theorie - Potenzfunktionen
3) Funktionen vom Typ y  x 2 n ; n  N 
DB:
x  ; x  0
y  ; y  0
WB:
Nullstelle:
keine
streng mon. w.:
  x  0
streng mon. f.:
0 x
gemeinsame Pkte.: P1(-1;1) und P2(1;1)
Graph:
Graphen dieser Funktionen heißen Hyperbeln, die aus 2
Hyperbelästen bestehen. Diese Hyperbeläste nähern sich
asymptotisch der x- bzw. y-Achse und sind achsensymmetrisch zur y-Achse.
Asymptoten:
y=0; x=0
Gymnasium „Am Thie“
Blankenburg
Theorie - Potenzfunktionen
4) Funktionen vom Typ y  x 2 n1 ; n  N 
DB:
x  ; x  0
y  ; y  0
WB:
Nullstelle:
keine
streng mon. w.:
nie
streng mon. f.:
   x  0 und 0  x  
gemeinsame Pkte.: P1(-1;-1) und P2(1;1)
Graph:
Graphen dieser Funktionen heißen Hyperbeln, die aus 2
Hyperbelästen bestehen. Diese Hyperbeläste nähern sich
asymptotisch der x- bzw. y-Achse und sind punktsymmetrisch zum Koordinatenursprung.
Asymptoten:
y=0; x=0
Gymnasium „Am Thie“
Blankenburg
Theorie - Potenzfunktionen
p
q
5) Funktionen vom Typ y  x ; p, q  Z ; p, q  0 (p nicht Vielfaches von q)
x  ; x  0
DB:
y  ; y  0
WB:
Nullstelle:
P(0;0)
streng mon. w.:
0 x
streng mon. f.:
nie
gemeinsame Pkte.: P1(1;1)
Symmetrie:
keine
Gymnasium „Am Thie“
Blankenburg
Theorie - Potenzfunktionen
p
q
6) Funktionen vom Typ y  x ; p, q  Z ; p  0, q  0 (p nicht Vielfaches von q)
x  ; x  0
DB:
y  ; y  0
WB:
Nullstelle:
keine
streng mon. w.:
nie
streng mon. f.:
0 x
gemeinsame Pkte.: P1(1;1)
Asymptoten:
y=0; x=0
Symmetrie:
keine