Näherungsverfahren (Word-Format

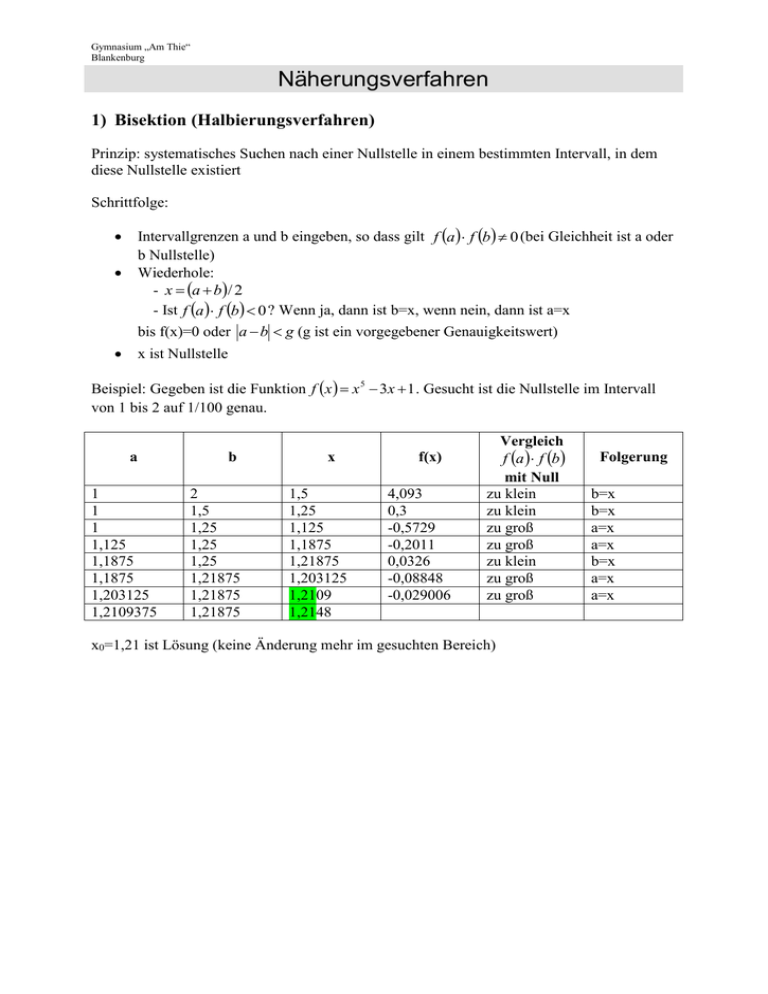
Gymnasium „Am Thie“
Blankenburg
Näherungsverfahren
1) Bisektion (Halbierungsverfahren)
Prinzip: systematisches Suchen nach einer Nullstelle in einem bestimmten Intervall, in dem
diese Nullstelle existiert
Schrittfolge:
Intervallgrenzen a und b eingeben, so dass gilt f a  f b  0 (bei Gleichheit ist a oder
b Nullstelle)
Wiederhole:
- x  a  b/ 2
- Ist f a f b  0 ? Wenn ja, dann ist b=x, wenn nein, dann ist a=x


bis f(x)=0 oder a  b  g (g ist ein vorgegebener Genauigkeitswert)

x ist Nullstelle
Beispiel: Gegeben ist die Funktion f x   x 5  3x  1 . Gesucht ist die Nullstelle im Intervall
von 1 bis 2 auf 1/100 genau.
a
1
1
1
1,125
1,1875
1,1875
1,203125
1,2109375
b
2
1,5
1,25
1,25
1,25
1,21875
1,21875
1,21875
x
1,5
1,25
1,125
1,1875
1,21875
1,203125
1,2109
1,2148
f(x)
4,093
0,3
-0,5729
-0,2011
0,0326
-0,08848
-0,029006
Vergleich
f a  f b
mit Null
zu klein
zu klein
zu groß
zu groß
zu klein
zu groß
zu groß
x0=1,21 ist Lösung (keine Änderung mehr im gesuchten Bereich)
Folgerung
b=x
b=x
a=x
a=x
b=x
a=x
a=x
Gymnasium „Am Thie“
Blankenburg
Näherungsverfahren
2)
Allgemeines Iterationsverfahren
Schrittfolge:
a) Festlegen eines geeigneten Startwertes x1
b) Berechnen von x   (x )
c) Bestimmen der Nullstelle durch xi 1   ( xi )
Beispiel: Gegeben ist die Funktion f x   x 3  3x 2  1 . Gesucht ist die Nullstelle im Intervall
von 2 bis 3 auf 1/100000 genau.
a) Geeigneter Startwert z.B. x1=2,8 (durch Zeichnung, Probieren etc.)
0  x 3  3x 2  1 /  x 2
b)
1
x 3 2  0
x
1
x  3  2    x  andere Möglichkeiten für x   (x ) sind z.B.
 x   3 3x 2  1 oder
x
x3 1
 x  
3x
c)
i
xi
f(xi)
1
2,8
-0,568
2
2,8725
-0,0524
3
2,87880
-0,00444
4
2,87934
-0,00034
5
2,87938
-0,0000398
6
2,879385
-0,000001835
x0=2,87938 ist Lösung
Vorteil: relativ geringer Rechenaufwand
Nachteil: eventuell Schwierigkeiten beim Bilden von x   (x)
Hinweis: Ein Iterationsvorgang muss nicht notwendigerweise zu Näherungslösungen führen,
er ist in diesem Fall divergent.
Gymnasium „Am Thie“
Blankenburg
Näherungsverfahren
3)
Newtonsches Näherungsverfahren
Schrittfolge:
a) Festlegen eines geeigneten Startwertes x0
b) Suchen der Ableitungsfunktion f’
c) Bestimmen der Nullstelle durch xn1  xn 
f xn 
(Newtonsche Rekursionsformel)
f ' xn 
Beispiel: Gegeben ist die Funktion f x   x 3  x  1 . Gesucht ist die Nullstelle auf 1/100000
genau.
a) Geeigneter Startwert z.B. x0=-0,5 (durch Zeichnung, Probieren etc.)
b) f x   3x 2  1
c)
n
xn
f(xn)
0
-0,5
0,375
1
-0,71
-0,068
2
-0,682969
-0,0015
3
-0,682328
-0,0000047
4
-0,6823278
-0,000000002
x0=-0,68232 ist Lösung
Herleitung des Newtonschen Näherungsverfahrens
Geometrische Überlegung
Wir betrachten das grün gezeichnete Dreieck mit den Katheten f(x1) und (x1 - x2), das das
Steigungsdreieck für die Tangente t1 an der Stelle x1 darstellt.
Gymnasium „Am Thie“
Blankenburg
Näherungsverfahren
Es gilt somit: tan   f  x1  
f x1 
x1  x2
x1  x2 
Durch Umformung entsteht
x2  x1 
f x1 
f x1 
f x1 
f x1 
Damit kann der erste Iterationsschritt durchgeführt werden und x2 berechnet werden,
anschließend auf dieselbe Art x3, ...
Allgemein ergibt sich: xn1  xn 
f xn 
f ' xn 
Bedingung: f x  0 , da sonst die Tangente parallel zur x-Achse verläuft und keinen
Schnittpunkt mit dieser ergibt - die Iteration bricht ab.
4)
Newtonsches Näherungsverfahren mit TR
Abschließend noch ein Trick, mit dessen Hilfe man unter Nutzung des TR sehr schnell die
Lösung findet, man darf sich nur nicht vertippen….
Schrittfolge analog zu oben:
a) Festlegen eines geeigneten Startwertes x0
b) Suchen der Ableitungsfunktion f’
c) Bestimmen der Nullstelle durch xn1  xn 
f xn 
(Newtonsche Rekursionsformel)
f ' xn 
Beispiel: Gegeben ist die Funktion f x   x 3  x  1 . Gesucht ist die Nullstelle.
a) Geeigneter Startwert z.B. x0=-0,5 (durch Zeichnung, Probieren etc.)
b) f x   3x 2  1
c) xn1  0,5 
x3  x  1
3x 2  1
d) Jetzt kommt der kleine aber feine Unterschied. Anstatt mit viel Rechenaufwand die Tabelle
zu erstellen, gibt man die unter c) gewonnene Formel in den Taschenrechner ein.
Für unser Beispiel ist das die Tastenfolge…
- 0 , 5 = - ( ALPHA = x³ + ALPHA = + 1 ) / ( 3 * ALPHA = x² + 1 ) =
Gymnasium „Am Thie“
Blankenburg
Näherungsverfahren
Anschließend drückt man = so oft hintereinander, bis die gewünschte Genauigkeit erreicht
ist. Für unser Beispiel lautet die Ergebnisreihe…
-0,714286714
-0,683179723
-0,682328423
-0,682327803
…
Hinweis: Für die Tastenkombination ALPHA = muss im Display des Taschenrechners ANS
erscheinen. Bei manchen Taschenrechnern geht das über die Kombi 2nd = . Wie zu sehen ist
muss man sich einfach nur merken, dass ANS an Stelle der Variablen steht und das =
zwischen dem Startwert und dem Minus vor der Klammer notiert werden muss. Auch dadurch
wird auf dem Display das ANS erzeugt.
Übungen:
Berechnen Sie die Nullstellen nach einem geeigneten Verfahren (Lösungen in Klammern)!
a)
b)
c)
d)
f ( x)  x 5  2
f ( x)  x  x
f ( x)  50 x 3  10 x 2  40 x
f ( x)  x 3  x
e) f ( x)  x 3  0,26 x 2  0,28x  5,568 I[-3;2]
f) f ( x)  x3  3x  5
6
2
g) 5  x  1  x 2
(1,14869835)
(-1/0/1)
(0/-0,8/1)
(0)
(-1,74)
(2,27901879)
(1,82211037)
weitere Anwendungen zum Newton-Verfahren
Taschenrechner verwenden das Verfahren zum Wurzelziehen, wir verwenden dazu folgende
Strategie (Bsp. gesucht ist die Wurzel aus 7 mit dem Newton-Verfahren)
1. x  7 , das ist definiert als positive Lösung der Gleichung
2. x 2  7 , wir betrachten die Zahl als positive Nullstelle der Funktion
3. f x   x 2  7
4. wir bilden die Ableitung f x   2 x , suchen uns einen Startwert, z.B. x0  1 , nutzen
das Verfahren und kommen auf x1  4; x2  2,875; x3  2,6549; x4  2,6458...
(Für einige Kritiker: ein kurzes Nachdenken führt zu dem besseren Startwert x0  2,5 )
Berechnen Sie die Wurzeln mit dem Newton-Verfahren (Kontrolle mit TR)!
a) x  2
b) x  3 2
c) x  5 100
d) x  10 10
Gymnasium „Am Thie“
Blankenburg
Näherungsverfahren
Das Newton-Verfahren kann auch verwendet werden, um die Schnittstelle zweier Funktionen
zu bestimmen.
Bsp.: Gesucht ist die Schnittstelle der Funktionen f x   x3 und g x   2  x .
1. wir ermitteln eine neue Funktion h(x) als Differenzfunktion der beiden
Ausgangsfunktionen (Idee: Gleichsetzen und auf einer Seite die Null erzeugen, die
andere Seite entspricht unserer Funktion), wir erhalten hx   x3  x  2
2. wir bilden die Ableitung hx   3x 2  1 , suchen uns einen Startwert, auch graphisch
durch Skizzieren der Ausgangsfunktionen (z.B. x0  1,5 ), nutzen das Verfahren und
kommen auf x1  1,5217391; x2  1,5217398; x3  1,5217397...
Übungen
LB. S.126/3, S.129/9 und 10