97u4v3 (application/msword 364.5 KB)

I Funktionen
Check-out: Klausurvorbereitung – Selbsteinschätzung
Checkliste „Funktionen“
Testaufgaben
1. Ich kann die Begriffe rund um
den Funktionsbegriff erklären
und anwenden.
Kann
ich
schon
Hilfen im
Buch, die man
bei Problemen
nacharbeiten
kann
Trainingsaufgaben
(Seitenangaben im
Buch)
1
Übersicht
auf S. 8
S. 37 A. 1 und
S. 38 A.14 in
Auszügen
2. Ich kann anhand des Graphen
erkennen, ob sie zu einer
Funktion gehören können oder
nicht.
2
Text zu Fig.
1 und Fig. 2
auf S. 8
S. 10 A. 6
3. Ich kann die Gleichung einer
Geraden in der Form
y = m · x + n bestimmen.
3
Beispiel 1
auf S. 11
S. 37 A. 3;
S. 199 A. 2d)
(Fig. 1) und
S. 199 A. 3 a)
4. Ich kann die Steigung einer
Geraden bestimmen, wenn der
Steigungswinkel gegeben ist,
und umgekehrt.
4
S. 40 Tipp
zu A. 25 auf
dem Rand
S. 40, A. 25
5. Ich kann den Schnittpunkt von
zwei Geraden bestimmen, die
in der Form y = m · x + n
gegeben sind.
5
6. Ich kann quadratische Gleichungen mithilfe der pq-Formel
lösen.
6
Beispiel 2
auf S. 12
S. 37 A. 4 und
S. 199 A. 4 b)
7. Ich kann Nullstellen von
Geraden und Parabeln
berechnen und die Ergebnisse
mithilfe des GTR überprüfen.
7
Beispiel 2
auf S. 12
S. 37 A. 4
8. Ich kann Schnittpunkte von
Geraden und Parabeln berechnen und die Ergebnisse
mithilfe des GTR überprüfen.
8
S. 37 A. 4(1)
und (2)
9. Ich kann mithilfe von quadratischen und linearen Funktionen Anwendungskontexte
beschreiben und Probleme im
Anwendungskontext lösen.
9
S. 39 A.19 und
20 sowie S. 40
A. 23
10. Ich kann den Verlauf des
Graphen von Potenzfunktionen
der Form f (x) = a · x n
skizzieren und zeichnen.
10
Merkkasten
sowie die
Figuren
unten auf
der S. 14
S. 40 A. 21
11. Ich kann bei einer ganzrationalen Funktion f das
Verhalten für x gegen unendlich
und x gegen minus unendlich
bestimmen.
11
Merkkasten
und Beispiel
auf S. 19
S. 37 A.2
© Ernst Klett Verlag GmbH, Stuttgart 2014 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.
Da bin
ich
fast
sicher
Ich bin
noch
unsicher
Kann
ich
noch
nicht
S. 37 A. 4 (1) und
(2) und S. 199
A. 4 a)
Autor: Thorsten Jürgensen-Engl
Checkliste „Funktionen“
Testaufgaben
12. Ich kann am Funktionsterm
ablesen, ob der Graph einer
ganzrationalen Funktion
achsensymmetrisch zur
y-Achse oder punktsymmetrisch zum Ursprung ist.
Kann
ich
schon
Hilfen im
Buch, die man
bei Problemen
nacharbeiten
kann
Trainingsaufgaben
(Seitenangaben im
Buch)
12
Merkkasten
2 auf S. 22
und Beispiel
1 auf S. 23
S. 37 A.8 und
S. 45 A. 7
13. Ich kann rechnerisch ermitteln,
ob der Graph einer Funktion
achsensymmetrisch zur
y-Achse bzw. punktsymmetrisch zum Ursprung ist.
13
Merkkasten
1 auf S. 22
und Beispiel
2 auf S. 23
S. 37 A.9
14. Ich kann am Funktionsterm
einer ganzrationalen Funktion
ablesen, wie viele Nullstellen
der Graph höchstens hat.
14
S. 27 oben:
Text zu
„Anzahl von
Nullstellen“
S. 39 A.16 und
S. 45 A. 8
15. Ich kann erkennen, wann die
Nullstellen einer ganzrationalen
Funktion durch Ausklammern
und Ablesen bestimmt werden
können und die Berechnung
durchführen.
15
Text auf
S. 26 und
Merkkasten
auf S. 27
S. 37 A.5 und 6
sowie S. 45 A. 1
16. Ich kann erkennen, wann die
Nullstellen einer ganzrationalen
Funktion mittels Substitution
bestimmt werden können und
die Berechnung durchführen.
16
Text auf
S. 26 sowie
Merkkasten
und Beispiel
1 auf S. 27
S. 37 A.7
17. Ich kann bei gegebenen
Funktionsgleichungen beschreiben, durch welche
Transformationen man den
Graphen der einen Funktion
aus dem Graphen der anderen
Funktion erhält.
17
Merkkasten
auf S. 32 und
Beispiel 1
auf S. 33
S. 37 A. 10 und
S. 45 A. 5
18. Ich kann zu einem gegebenen
Funktionsgraphen den Funktionsterm angeben, wenn von
einer transformierten Funktion
der Graph und der Term
bekannt sind.
18
Merkkasten
auf S. 32 und
Beispiel 2
auf S. 33
S. 38 A.12 und
S. 45 A. 5
© Ernst Klett Verlag GmbH, Stuttgart 2014 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.
Da bin
ich
fast
sicher
Ich bin
noch
unsicher
Kann
ich
noch
nicht
Autor: Thorsten Jürgensen-Engl
I Funktionen
Check-out: Klausurvorbereitung – Test- und Trainingsaufgaben
1 a) Drücken Sie die Aussagen in mathematischer Kurzschrift aus.
(1) Die Funktion g nimmt an der Stelle 5 den Funktionswert 12 an.
(2) Die Zahl 3 gehört nicht zur Definitionsmenge der Funktion f.
(3) Alle Funktionswerte der Funktion g sind positiv.
b) Beschreiben Sie unter Verwendung der Fachsprache, was man unter einer Definitionslücke versteht.
c) Geben Sie für die Funktion f mit f (x) = 5 2 die Definitionsmenge an und skizzieren Sie den Graphen
1 x
mithilfe des GTR.
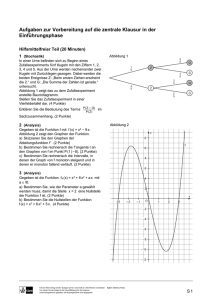
2 Entscheiden Sie, ob der abgebildete Graph zu einer Funktion gehören kann. Begründen Sie Ihre Antwort.
a)
b)
c)
3 a) Bestimmen Sie die Gleichungen der
abgebildeten Geraden in der Normalform
y = m · x + n.
b) Bestimmen Sie die Gleichung der Geraden in der
Form y = m · x + n.
(I) m = 2; die Gerade verläuft durch P (3 | 7)
(II) m = − 1,5; die Gerade verläuft durch Q (− 1 | − 4)
c) Bestimmen Sie die Gleichung der Geraden, die
durch die Punkte A und B verläuft, in der Form
y = m · x + n.
(I) A (2 | 4); B (3 | 8)
(II) A (6 | − 2); B (9 | − 9)
4 a) Bestimmen Sie die Steigung der Geraden mit dem Steigungswinkel .
(I)  = 60°
(II)  = 150°
b) Bestimmen Sie den Steigungswinkel  der Geraden
(I) g mit y = 2 x + 3.
(II) h mit y = − x + 4.
5 Bestimmen Sie den Schnittpunkt der Geraden f und g bei a) zeichnerisch und bei b) rechnerisch.
a) f mit y = 3 x − 4 und g mit y = − 2 x + 6
b) f mit y = − 2 x + 11 und g mit y = 5 x + 1
6 Geben Sie die Lösungen der quadratischen Gleichungen an.
a) x2 − 13 x + 7 = 0
c) 1,5 x2 + 36 = 5 x
© Ernst Klett Verlag GmbH, Stuttgart 2014 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.
b) 3 x2 − 4 x − 4,4 = 0
d) 3 x2 = 5 x − 25
2
2
24
Autor: Thorsten Jürgensen-Engl
7 Bestimmen Sie die Nullstellen der angegebenen Funktionen.
a) g (x) = 2 x + 2
b) f (x) = 4 x2 − 16
c) f (x) = x2 − 24 x
d) f (x) = 2 x2 − 4 x − 6
8 Bestimmen Sie die Schnittpunkte der Funktionen f mit f (x) = x2 + 5 x + 4 und g mit g (x) = 0,5 x + 1.
9 Die Flugkurve eines Speers kann mithilfe der Funktion h mit h (x) = − 0,02 x2 + 0,8 x + 1,8 beschrieben
werden x und h (x) in m .
a) Was bedeutet h (0) im Anwendungskontext?
b) Wie weit fliegt der Speer?
c) Wie hoch ist der Speer in seinem höchsten Punkt?
10 a) Beschreiben Sie den Verlauf des Graphen der Funktion f mit f (x) = 0,25 x5.
b) Wie muss man die „Y-Bereiche“ beim GTR einstellen, damit der Graph im Intervall − 4 ≤ x ≤ 2 vollständig
zu sehen ist?
11 Bestimmen Sie das Verhalten von f für x   .
a) f (x) = 3 x7 − 4 x4 + 5
b) f (x) = 0,25 x5 − 8 x6 − x
12 Untersuchen Sie die Symmetrieeigenschaft des Graphen der Funktion f.
a) f (x) = − x10 + 0,6 x8 + 10
b) f (x) =
13 Untersuchen Sie die Funktion f mit f (x) =
1
3
· x5 + 2 x − 7
x
x2  1
c) f (x) = 2 x9 − x3 + x
auf Symmetrie.
14 Ermitteln Sie, wie viele Nullstellen die Funktion f höchstens hat.
a) f (x) = x5 − 3 x2 + 3
b) f (x) = 3 x2 − 0,5 x6 + x3 + 8000
15 Entscheiden Sie zunächst, ob man die Nullstellen der Funktion f durch Ablesen bzw. durch Ausklammern
ermitteln kann und bestimmen Sie diese, wenn eines dieser Verfahren funktioniert.
a) f (x) = x (x − 4) (2 x + 8)
b) f (x) = 12 x − 3 x3
c) f (x) = x3 + 13 x4 + 8
16 Entscheiden Sie zunächst, ob man die Nullstellen der Funktion f mithilfe des Substitutionsverfahrens
ermitteln kann und bestimmen Sie diese, wenn das Verfahren funktioniert.
b) f (x) = 1 x4 − 3 x2 + 2
a) f (x) = x4 + 2 x3 + 5
4
c) f (x) = x6 − 10 x3 + 9
17 Gegeben ist die Funktion f mit f (x) = x3 − 4 x. Geben Sie an, wie man den Graphen der Funktion g mit


g (x) = − 2  (x  3)3  4 (x  3) aus dem Graphen der Funktion f erhält.
18 Gegeben ist die Funktion f mit
f (x) = − x4 + 2 x2. Man erhält in der
nachfolgenden Abbildung den Graphen von g,
wenn man den Graphen von f in y-Richtung
streckt und verschiebt. Beschreiben Sie die
Streckung und Verschiebungen.
© Ernst Klett Verlag GmbH, Stuttgart 2014 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.
Autor: Thorsten Jürgensen-Engl
I Funktionen
Check-out: Klausurvorbereitung – Test- und Trainingsaufgaben –
Lösungen
1 a) (1) f (5) = 12; (2) Df =
\ {3} und (3) W g = +
b) Eine Definitionslücke stellt im Definitionsbereich einen x-Wert dar,
für den die Funktion nicht definiert ist – das heißt, für den man keinen
Funktionswert bestimmen kann.
c) Aus 1 − x2 = 0 bzw. x = + 1 oder x = − 1 ergeben sich die
Definitionslücken x1 = 1 und x2 = − 1.
Demnach ist Df = \ {− 1; 1}.
2 a) Der Graph gehört zu einer Funktion, da jedem x-Wert genau ein y-Wert zugeordnet ist.
b) Der Graph gehört nicht zu einer Funktion, da es x-Werte gibt, denen mehrere y-Werte zugeordnet sind
(es gibt zur y-Achse parallele Geraden, die den Graphen mehrfach schneiden).
c) Der Graph gehört nicht zu einer Funktion, da es bei x = 1 (zwei Kästchen in positive x-Richtung) einen
x-Wert gibt, dem mehrere y-Werte zugeordnet sind (hier schneidet die zur y-Achse parallele Gerade, den
Graphen mehrfach).
3 a) f mit y = x + 2; g mit y = − 2 x + 4; h mit y = − 1 x + 1
3
b) (I) y = 2 x + 1
(II) y = − 1,5 x − 5,5
c) (I) y = 4 x − 4
(II) y = −
4 a) (I) m ≈ 1,73
(II) m ≈ − 0,58
7
3
x + 12
b) (I)  ≈ 63,43°
(II)  ≈ − 45° = 135°
5 a) zeichnerische Lösung: S (2 | 2)


b) rechnerische Lösung: S  10 57  .
 7
7 
6 a) x1 ≈ 12,44 und x2 ≈ 0,56
b) x1 ≈ 2,05 und x2 ≈ − 0,71
c) Es gibt keine Lösungen.
d) x = 5 (Es gibt nur eine Lösung.)
7 a) x = − 1
c) x1 = 0 und x2 = 24
b) x1 = − 2 und x2 = 2
Überprüfung mithilfe des GTR über die „zero“-Funktion.
6
d) x1 = − 1 und x2 = 3
8 Die Schnittpunkte liegen bei den Stellen x1 ≈ − 0,814 und x2 ≈ − 3,686.
Damit erhält man die Schnittpunkte als Näherungswerte:
S1 (≈ − 0,814 | ≈ 0,593) und S2 (≈ − 3,686 | ≈ − 0,843).
Überprüfung mithilfe des GTR, indem man die neue Funktion d (x) = f (x) − g (x) eingibt und von dieser neuen
Funktion die Nullstellen mithilfe der „zero“-Funktion bestimmt.
(Denn aus f (x) = g (x) folgt durch Umformen f (x) − g (x) = 0.)
© Ernst Klett Verlag GmbH, Stuttgart 2014 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.
Autor: Thorsten Jürgensen-Engl
9 a) h (0) = 1,8 entspricht der Höhe des Speers bei einer Entfernung von 0 m vom Abwurfpunkt. Also
entsprechen 1,8 m der Abwurfhöhe, die beim Speerwurf etwa der Kopfhöhe des Werfers entspricht.
b) Die Nullstellen der Funktion sind x1 ≈ 42,14 und x2 ≈ − 2,14. Für den Speerwurf ist nur die Nullstelle x1
interessant, da x2 negativ ist. Der Speer wird also etwa 42,14 m weit geworfen.
c) Die Höhe am höchsten Punkt entspricht dem y-Wert des Scheitelpunktes von h. Die Scheitelpunktsform
lautet: h (x) = − 0,02 (x − 20)2 + 9,8. Demnach hat der Speer in seinem höchsten Punkt eine Höhe von 9,8 m.
10 a) Für negative x-Werte liegen die Funktionswerte im negativen
Bereich und für positive x-Werte liegen die Funktionswerte im positiven
Bereich. Der Graph verläuft durch den Ursprung des Koordinatensystems O (0 | 0).
b) f (− 4) = − 256 und f (2) = 8. Demnach muss die y-Achse von ca.
− 260 bis 10 dargestellt werden.
11 a) f (x)  +  für x  +  und f (x)  −  für x  − 
b) f (x)  −  für x  +  und f (x)  −  für x  − 
12 a) Der Graph ist achsensymmetrisch zur y-Achse (gerade Funktion).
b) Der Graph ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
c) Der Graph ist punktsymmetrisch zum Ursprung.
13 Der Graph der Funktion ist punktsymmetrisch zum Ursprung (0 | 0), da f (− x) = − f (x) gilt.
14 a) höchstens 5 Nullstellen
b) höchstens 6 Nullstellen
15 a) Die Nullstellen sind x1 = 0, x2 = 4 und x3 = − 4.
b) Die Nullstellen sind x1 = 0, x2 = 2 und x3 = − 2.
c) Bei dieser Funktion kann man weder das Verfahren des Ablesens noch das des Ausklammerns anwenden.
16 a) Das Substitutionsverfahren ist hier nicht anwendbar.
b) x1 ≈ – 3,36; x2 ≈ 3,36; x3 ≈ – 0,84; x4 ≈ 0,84
2
c) x1 = 1 und x2 = 3 3 ≈ 2,0801
17 Der Graph von f wird an der x-Achse gespiegelt, mit dem Faktor 2
gestreckt und um 3 Einheiten nach rechts verschoben.
18 Man erhält den Graphen von g, indem man den Graphen von f mit dem Faktor 2 in y-Richtung streckt und
anschließend um zwei Einheiten nach unten verschiebt.
Es ist g (x) = 2 · (– x4 + 2 x2) – 2.
© Ernst Klett Verlag GmbH, Stuttgart 2014 | www.klett.de | Alle Rechte vorbehalten
Von dieser Druckvorlage ist die Vervielfältigung für den eigenen
Unterrichtsgebrauch gestattet. Die Kopiergebühren sind abgegolten.
Autor: Thorsten Jürgensen-Engl