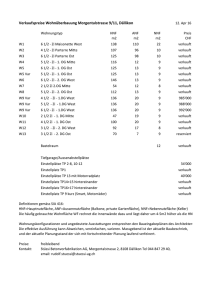
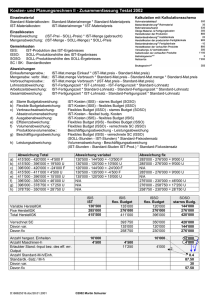
Die Aggregationsfragestellung

Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 1
Die Aggregationsfragestellung
Die Aggregations- bzw. Aggregierungsfragestellung (manchmal auch Aggregations- bzw. Aggregierungsproblem genannt) ist die Fragestellung nach der Gleichheit des Zusammenhangs zwischen gleichartigen
Variablen auf unterschiedlichen Ebenen. Als gleichartige Variable auf der höheren Ebene gilt die Aggregatsvariable, d. h. die Mittelwerte der Variablen, aggregiert jeweils über die Einheiten der niedrigen Ebene, soweit
sie der Einheit der höheren Ebene angehören.
Falls eine solche Gleichheit gilt, erlauben Untersuchungen
auf höherem Niveau Rückschlüsse auf die Zusammenhänge
auf niedrigerem Niveau (falls etwa die Daten auf der niedrigeren Stufe nicht zur Verfügung stehen).
Falls die Zusammenhänge nicht gleich sind, fälschlicherweise aber Gleichheit unterstellt wird, ist der Schluss vom Zusammenhang auf der höheren Ebene auf die niedrigere Ebene
ein Fehlschluss, der als ökologischer Fehlschluss bezeichnet
wird. Der Zusammenhang auf der höheren Ebene wird auch
als ökologischer Zusammenhang (bzw. ökologische
Korrelation) bezeichnet.
Z.B. Bei Analysen des Wahlverhaltens stehen für alle
Zählbezirke die Anteile der Wahlen unterschiedlicher
Parteien zur Verfügung, nicht aber ohne Zusatzbefragung die
individuellen Wahlentscheidungen. Inwiefern ist es möglich,
aus den Zusammenhängen auf Zählbezirksebene auf
individuelles Wahlverhalten zu schließen?
Z.B. Eine der ersten empirischen Untersuchungen in der
Soziologie ist die von EMILE DURKHEIM durchgeführte
Suicidstudie; dabei hat DURKHEIM auf Kantonsdaten
(durchschnittliche Haushaltsgröße, durchschnittliches Alter,
Anteil der Katholiken, Suicidanteil) basierende
Zusammenhänge im Sinne individueller Zusammenhänge
interpretiert.
Ursprünglich wurde nur untersucht, inwiefern der Korrelationskoeffizient zwischen zwei Variablen x und y in
unterschiedlichen Aggregationsebenen (siehe YULE G. U. & KENDALL M. G. (1964, 4. Auflage), diese Abhandlung ist 1950 in erster Auflage erschienen und geht zurück auf noch frühere Versionen).
YULE & KENDALL stellen fest, dass bei fortlaufender
Zusammenfassung der Einheiten (Counties) der
Korrelationskoeffizient ‚beliebig’ groß gemacht werden
kann und fragen daher, ob dann die Korrelation überhaupt
noch ein sinnvolles Maß für den Zusammenhang der
ursprünglichen Merkmals ist. Diese Aussage kann als
Korrelationsinflationshypothese bezeichnet werden.
In Kapitel 13 unter der Überschrift The modifiable Unit untersuchen YULE & KENDALL den Ertrag von Weizen und
Kartoffeln pro ‚Morgen’ für 48 englische Counties aus dem
Jahr 1936. Die Korrelation ist 0.2189.
Bei Zusammenfassung nebeneinanderliegender Counties auf
nur noch 24 Einheiten ist die Korrelation 0.2963, bei
Zusammenfassung auf zwölf ist die Korrelation 0.5757, bei
Zusammenfassung auf 6 Einheiten ist die Korrelation 0.7649,
bei Zusammenfassung auf 3 Einheiten ist die Korrelation
0.9902.
Dieselbe Frage kann auch bezüglich anderer Maße des Zusammenhangs, der Kovarianz (bzw. des Kreuzprodukts) zwischen zwei Variablen oder des Regressionskoeffizienten, gestellt werden.
Der Einfachheit halber soll zuerst der Zusammenhang zwischen zwei Variablen auf nur zwei Ebenen betrachtet
werden.
Zusammenhang auf zwei Ebenen
Bezeichnungen auf der 1. Ebene
Bezeichnung: Gegeben seien J Gruppen (2. Ebene); in jeder
Gruppe seien eventuell unterschiedlich viele Einheiten der 1.
Ebene vorhanden (=nj).
Die Messwertpaare für jede Einheit der ersten Ebene seien:
(yij, xij) mit j = 1, ... , J und i=1, ... , nj.
Der erste Index nummeriert die UE1 innerhalb der Einheiten
der 2. Ebene, der 2. Index kennzeichnet die Einheiten der 2.
Ebene.
Beispiel: 10 Personen seien
in 3 Gruppen (J=3) zusammengefasst.
Dabei ist n1=5, n2=3, n3=2.
Die Bezeichnungen und Werte
sind rechts aufgeführt:
y11
y 21
y 31
y 41
y 51
y12
y 22
y 32
y13
y 23
x11
x 21
x 31
x 41
x 51
x12
x 22
x 32
x13
x 23
=
5
5
5
4
1
4
2
3
1
0
3
2
1
2
2
2
4
3
0
1
5
5
5
4
1
4
2
3
1
0
3
2
1
2
2
2
4
3
0
1
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 2
Bezeichnungen auf der 2. Ebene (der Mittelwerte der Variablen)
Für alle J Gruppen (2. Ebene) werden die Mittelwerte
Beispiel: Mittelwerte der 3
berechnet: (y.j, x.j) mit j = 1, ... , J
mit: y  j 
1
nj
ij1 y ij
n
und x  j 
1
nj
Gruppen (J=3) zusammengefasst.
ij1 x ij
n
y 1
x 1
y 2
x 2
y 3
x 3
=
4
3
0 .5
2
3
0 .5
Alle Operationen (z.B. Mittelwertbildungen usw.) auf der 2. Ebene werden jeweils mit der Gruppengröße
gewichtet.
Daher sind auch die Gesamt-Mittelwerte gleich groß für die
Berechnung auf erster oder zweiter Ebene
y  
1
n
 j1 i j1 y ij  n1 ij1 n j y  j ; entsprechend für x.
J
n
n
Gesamt-Mittelwerte für y:
y  = (5 +5 +5 +4 +1 +4 + 2 +3
+1 +0)/ 10 = (5*4 + 3*3 +2*0.5)/10 = 3.
Gesamt-Mittelwert für x: x  = (3+2+...+0+1)= (5*2+ 3*3
+ 2*0.5)/10 = 2.
Kreuzproduktsummen, Kovarianzen und Varianzen
Ebene 1
Ebene 2 (Gruppen)
6
6
5
yj 5
Mean(y)
y ij 4
3
y
Zur Beschreibung des Zusammenhangs
der Variablen auf den unterschiedlichen
Ebenen bietet sich der
Korrelationskoeffizient an. Er baut auf
den Kovarianzen bzw. auf den
Kreuzproduktsummen auf.
2
3
2
1
1
Die Kreuzproduktsumme zur
Beschreibung des Zusammenhangs
zwischen x und y für die Ebene eins soll
hier als Total-Kreuzproduktsumme
(= CPxy ,T ), jene für Ebene zwei als
4
0
0
-1
-1
-1
0
1
2
x1
3
4
-1
5
0
1
2
3
4
5
xj
Mean(x1)
x ij
Between-Kreuzproduktsumme(= CPxy ,B )bezeichnet werden.
Die beiden Kreuzproduktsummen stehen dabei zueinander in folgender Beziehung:
Kreuzprodukt-Additionssatz: Die Total-Kreuzproduktesumme ist gleich der Summe aus
Between-Kreuzproduktesumme und Within-Kreuzproduktesumme: CPxy ,T = CPxy ,B + CPxy ,W .
2
1
Zusammenhang dar, der summarisch innerhalb der Gruppen besteht;
sie ist die Kreuzproduktsumme für das Streudiagramm, bei dem alle x-yWerte pro Gruppe zentriert werden (von jedem Wert wird der
entsprechende Gruppenmittelwert subtrahiert). Geometrisch bedeutet das
eine Verschiebung aller Punktpaare derart, dass die Gruppenmittelwerte in
den Nullpunkt verschoben werden.
YZent
Die Within-Kreuzproduktesumme (= CPxy , W ) stellt dabei den
0
-1
-2
-3
-4
-1.5
-1
-0.5
0
.5
1
X1zent
Beispiel: CPxy ,B (= 7.5) zeigt hier den positiven
Die Formeln der verschiedenen Kreuzproduktarten sind:
 y  )(x ij  x  ) .
 
J
CPxy ,B =  j1 n j ( y  j  y  )( x  j  x  )
J
nj
CPxy , W =  j1 i 1 ( y ij  y  j )(x ij  x  j )
CPxy ,T =
J
j1
nj
( y ij
i 1
Zusammenhang auf Gruppenebene (Ebene 2). Der
Zusammenhang auf Ebene 1 ( CPxy ,T =5) erweist sich
ebenfalls als positiv.
Innerhalb der Gruppen ist aber in den obigen Punktwolken
auf Ebene 1 eine Tendenz zu negativem Zusammenhang
erkennbar ( CPxy , W = -2.5)
Nach dem Kreuzproduktadditionssatz gilt: 5 = 7.5 + (-2.5)
1.5
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 3
Auch bei den Kovarianzen zwischen x und y wird unterschieden zwischen einer Total-Kovarianz für Ebene 1,
einer Between-Kovarianz für Ebene 2 und einer Within-Kovarianz für die Kovarianz, die innerhalb der Gruppen
besteht. Die Kovarianzen sind die durch die Freiheitsgrade dividierten Kreuzprodukte.
Auch die Varianzen können auf Kreuzprodukte zurückgeführt werden, und zwar auf Kreuzprodukte der
Variablen mit sich selbst; die Kreuzproduktsummen der Variablen mit sich selbst sind die Quadratsummen. So
kann etwa die Gesamtvarianz für x (=Var(x)) als CP xx ,T / (n-1) geschrieben werden. Auch hier können
wiederum die drei Typen von Varianzen unterschieden werden (Total, Between und Within).
Formeln der verschiedenen Quadratsummen sind
 j1 ij1 ( y ij  y  )(y ij  y  ) .
J
Between: CPyy,B =  j1 n j ( y  j  y  )( y  j  y  )
J
n
Within: CPyy, W =  j1 i j1 ( y ij  y  j )(y ij  y  j ) ;
J
Total: CPyy,T =
n
analog ebenfalls für x.
Beispiel: Die Quadratsumme in y in dieser Schreibweise ist
CPyy,B = 17.5 ; in x CP xx , B = 7.5 .
Die Quadratsummen auf Ebene 1 sind
CPyy,T = 32 und CP xx ,T = 12.
Die Quadratsummen innerhalb der Gruppen sind
CPyy, W = 14.5 und CP xx , W = 4.5
Auch hier gilt der Kreuzproduktadditionssatz, für y
32 = 17.5 + 14.5 und für x 12 = 7.5 + 4.5.
Korrelationen
Bei den Korrelationen auf den beiden Ebenen können wiederum die Total-Korrelation (für die Korrelation auf
Ebene 1) und die Between-Korrelation (sie wird auch als ökologische Korrelation bezeichnet) unterschieden
werden. Die Korrelationen sind normierte Kovarianzen (die Kovarianzen werden durch die
Standardabweichungen der beiden Variablen dividiert). Sie können auch in diesem Sinn als normierte
Kreuzprodukte dargestellt werden.
Die Formeln der verschiedenen Korrelationen:
=
rxy ,T
rxy ,T =
CP xx ,T CP yy,T
rxy ,B =
rxy , W
Beispiel: Korrelation auf Ebene 1 zwischen x und y ist
CP xy ,T
= 0.2552.
Die Korrelation auf Ebene 2 zwischen rxy, B =
CP xy , B
7.5
17.5*7.5
=
0.65 ist hier viel größer als auf Ebene 1.
CP xx , B CP yy, B
Die Within-Korrelation rxy , W =
CP xy , W
=
5
32*12
2.5
14.5*4.5
= - 0.31
charakterisiert den im Streudiagramm sichtbaren
Zusammenhang der gruppenzentrierten Wertepaare als leicht
negativ.
CP xx , W CP yy, W
Die Beziehung zwischen den Korrelationen auf den unterschiedlichen Ebenen ist etwas komplizierter als die für
die Kreuzprodukte, sie wurde von ROBINSON(1950) entdeckt:
rxy ,T  rxy ,B  y|G  x|G  rxy , W 1   2y|G
1   2x|G
Beispiel: Korrelation zwischen dem x-Merkmal und y:
0.2552 = 0.65 * 0.58 - 0.31* 0.41
 2y|G ist der Determinationskoeffizient 1. Art für die Prädiktion der y-Werte
auf Grund der Gruppenmittel (=
CP yy, B
Die beiden Determinationskoeffizienten 1. Art sind:
),
CP yy,T
entsprechend  x|G für x (=
2
CP xx ,B
).
 2y|G =0.547 (= 1732.5 )
bzw.
 2x|G =0.625 (= 712.5 )
CP xx ,T
Regression
Als Maße des Zusammenhangs werden in erster Linie die Steigungen auf beiden Ebenen betrachtet und deren
Schätzfehler, zudem auch die Möglichkeit der Schätzung der Störgrößenvarianz auf beiden Ebenen.
Steigungs-Regressionskoeffizienten
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 4
Während die Korrelationskoeffizienten beschreiben, wie gut eine Gerade die Steigung beschreibt, charakterisiert
der Regressionskoeffizient die Steigung selbst. Die Modellgleichung etwa für die 1.Ebene lautet:
y ij  a yx,T  b yx,T x ij  e ij (mit eij als Störgrößen). Auch für die 2. Ebene (der Mittelwerte) könnte eine
Modellgleichung formuliert werden: y  j  a yx,B  b yx,B x  j  e  j . Insgesamt können drei Arten von
Steigungskoeffizienten unterschieden werden, für die hier die Schätzer berichtet werden:
Schätzer der Steigungen:
=
b̂ yx,T
CP xx ,T
b̂ yx,B =
b̂ yx, W
Beispiel: Steigung auf Ebene 1 für y pro x-Einheit ist
CP xy ,T
=
CP xy , B
CP xx , B
CP xy , W
CP xx , W
b̂ yx,T =
. (Kurzbezeichnung: b̂ T )
5
12
= 0.417.
Die Steigung auf Ebene 2 zwischen b̂ yx, B = 77..55 = 1 ist
hier viel größer als auf Ebene 1.
. (Kurzbezeichnung: b̂ B )
Die Within-Steigung b̂ yx, W = 42.5.5 = - 0.55 charakterisiert
den im Streudiagramm sichtbaren Zusammenhang der
gruppenzentrierten Wertepaare als leicht negativ.
. (Kurzbezeichnung: b̂ W )
Die Beziehung zwischen den Steigungen auf den unterschiedlichen Ebenen ist zwar komplizierter als für die der
Kreuzprodukte, aber einfacher als die für die Korrelationen:
Beispiel: Die Steigung auf Ebene 1 ist
b̂ yx,T  b̂ yx,B  2x|G  b̂ yx, W (1  2x|G )
5
12
 2x|G ist wiederum der Determinationskoeffizient 1. Art für die Prädiktion
der x-Werte auf Grund der Gruppenmittel (=
CP xx ,B
).
Denn: Die Beziehung zwischen den Kreuzprodukte ist CPxy ,T = CPxy ,B
CP xy ,T
CP xx ,T

CP xy , B CP xx , B
CP xx , B CP xx ,T
7 .5
7 .5
7 .5
.5
+ 42.5.5 (1- 712
).
12
Der Determinationskoeffizienten 1. Art ist:
 2x|G =0.625
.5
(= 712
)
CP xx ,T
Ergänzen bei den Summanden ergibt
=

+ CPxy , W . Dividieren durch CPxy ,T und jeweiliges
CP xy , W CP xx , W
. Einsetzen der Definitionen für die
CP xx , W CP xx ,T
Steigungen und der Determinationskoeffizienten liefert das Ergebnis. Qed
Der Between-Steigungsschätzer kann erwartungstreu sein.
Dass die Total- und Between-Steigungsschätzer recht unterschiedliche Ergebnisse
liefern, wurde an Hand des obigen Beispiels demonstriert.
Trotzdem kann gezeigt werden, dass der Between-Steigungsschätzer ein
erwartungstreuer Schätzer für den Total-Steigungsparameter sein kann, und zwar:
Satz der erwartungstreuen, aggregierten Schätzung der Steigung: Unter der
Annahme, dass die y-Werte originär auf Grund des Modells auf der 1. Ebene
entstehen y ij  a yx  b yx x ij  e ij liefert der Between-Steigungsschätzer im
Schnitt über alle möglichen Replikationen den wahren Parameter der 1. Ebene,
formal in Erwartungswertausdrucksweise: E( b̂ yx,B ) = byx; Voraussetzung dafür
ej
yj
Between
2.Ebene
xj
eij
yij
xij
byx
ayx
Total
1.Ebene
ist zudem, dass auch die aggregierten Störgrößen nicht mit den aggregierten xVariablen kovariieren.
Standardfehler der geschätzten Steigung
Der Standardfehler der geschätzten Steigung ist die Wurzel der Varianz der geschätzten Steigung. Der Vergleich
der beiden Schätzer (Between-Steigung und Total-Steigung) zeigt, dass die auf der Ebene 1 geschätzte Steigung
i.a. einen kleineren Standardfehler hat als die auf der aggregierten Ebene 2 (bei bekannter Varianz der
Störgröße). Das bedeutet, dass die Konfidenzintervalle für die Steigung bei Schätzung auf Ebene 1 schmaler
sind und ebenfalls eher signifikant werden.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 5
Die Varianz der geschätzten Steigung auf Ebene 1 ist
 e2
Var( b̂ yx,T ) =
CP xx ,T
Beispiel: Die Varianz des Schätzers von byx auf Ebene 1 ist
Die Varianz der geschätzten Steigung auf Ebene 2 ist
 e2
Var( b̂ yx, B ) =
CP xx ,B
Die Varianz des Schätzers von byx auf Ebene 2 ist hier
hier Var( b̂ yx,T ) =
Var( b̂ yx, B ) =
 e2
12
 e2
7 .5
CP xx ,T .
 e2
2
wird  e durch 12
12
2
dividiert, bei der Var( b̂ yx, B ) wird  e nur durch 7.5
Daher gilt Var( b̂ yx,T ) < Var( b̂ yx, B ), falls die Within-
dividiert; daher ist Var( b̂ yx,T ) kleiner.
Wegen CP xx ,T = CP xx , B + CP xx , W , wobei die CPs hier
positive Quadratsummen sind, ist CP xx , B i. a. kleiner als
Beispiel: Bei der Var( b̂ yx,T ) =
Quadratsumme größer als 0 ist.
Schätzung der Störgrößenvarianz
Oben wurde die Varianz der Störgröße (=  e2 ) als bekannt vorausgesetzt; sie muss i. a. ebenfalls geschätzt
werden. Sie kann wiederum auf beiden Ebenen erwartungstreu geschätzt werden.
Schätzformel der Störgrößenvarianz auf Ebene 1 ist
2


CP xy
,T 
/(n  2) , wobei n die Anzahl der
̂ e2 =  CP yy,T 

CP xx ,T 


Einheiten auf Ebene 1 ist.
Schätzformel der Störgrößenvarianz auf Ebene 2 ist
2


CP xy
,B 

2
=
CP

/(G  2) , wobei G die Anzahl der
̂ e
yy
,
B

CP xx ,B 


Einheiten auf Ebene 2(=Gruppenanzahl) ist.


Beispiel: Die Störgrößenvarianzschätzung auf Ebene 1 liefert
25
̂ e2 = 32  12 /(10  2) = 29.92 / 8 = 3.74.
Die Anzahl der Einheiten auf Ebene 1 ist 10 (=n).

/
Die Störgrößenvarianzschätzung auf Ebene 2 liefert
̂ e2 = 17.5 
56.25
7.5
(3  2) = 10 / 1 = 10
Die Anzahl der Einheiten auf Ebene 2 ist 3 (=G).
Eine Aussage darüber, welche Schätzung
tendenziell eine größere Fehlervarianz liefert, ist
für den allgemeinen Fall nicht möglich.
Zusammenhang von Variablen zweier Ebenen
Als zwischen den beiden Ebenen vermittelnder Zusammenhang soll nun der zwischen den Werten der 1. Ebene
und Mittelwerten kurz untersucht werden. Der Einfachheit halber sollen für die 1. Ebene der y-Wert und für die
2. Ebene der Gruppenmittelwert für y und x betrachtet werden.
Kreuzprodukte
Das Kreuzprodukt CP y j , x  j zwischen einer
Mittelwertvariablen (hier x  j ) mit einer andern
Mittelwertvariablen (hier y  j ) ist gleich dem Kreuzprodukt
CP y, x  j zwischen der Mittelwertvariable (hier x  j ) und der
entsprechenden Variablen auf Ebene 1 (hier y ij ).
Beispiel: Über die
behauptete
Eigenschaft, dass
CP y , x (=7.5 )
Matrix der Kreuzprodukte
y
y j
xj
y
32
17.5
7.5
y j
17.5
17.5
7.5
j
gleich
j
CP y, x  j (=7.5)
xj
7.5
7.5
7.5
ist, hinaus können in
der Tabelle der Kreuzprodukte noch weitere Gleichheiten
entdeckt werden.
Für diese und andere Gleichheiten sind die Beweise im Anhang zu finden.
Die Kreuzprodukte mussten hier etwas anders bezeichnet werden als oben, da Variablen aus unterschiedlichen
Ebenen involviert sind. Für die Spezialfälle mit Variablen aus gleichen
Ebene 2 (Gruppen)
Ebenen könnte weiterhin die vorherige Bezeichnung verwendet werden,
6
etwa CP y j , x  j = CPxy ,B oder CP x  j , x  j = CP xx , B .
y ij 5
4
y
Ebene 1
3
2
1
0
-1
-1
0
1
2
x1mean
xj
3
4
5
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 6
Regression
Als Regression soll hier die Prädiktion der y-Werte der ersten Ebene durch die x-Mittelwerte untersucht werden
Der Steigungsregressionskoeffizient ist hier gleich wie im obigen Between-Modell wegen der Gleichheit von
CP y j , x  j und CP y, x  j .
Der Koeffizient ist b̂ yx j =
CP y, x  j
= (wegen der Gleichheit des Zählerkreuzprodukts) =
CP x  j , x  j
CP xy , B
.
CP xx , B
Korrelation
Andererseits ist die Korrelation zwischen x  j und y nicht gleich der Korrelation zwischen x  j und y  j ,
rx  j , y
CP y j , x  j
=
CP x  j , x  j CP yy
rxy ,between = rx  j , y  j =
CP y j , x  j
CP x  j , x  j CP y j , y j
Da CPyy größer oder gleich CP y j , y j ist,
Beispiel: Korrelation zwischen y und den -Mittelwerten
ist r x , y =
j
7.5
7.5*32
=0.484.
Die Korrelation zwischen x und y auf Ebene 2 zwischen
rxy,between =
7.5
17.5*7.5
= 0.65 ist viel größer als r x , y
j
ist rxy ,B größer oder gleich rx  j , y .
Der Determinationskoeffizient 2. Art ist (bei nur einem Prädiktor) gleich der quadrierten Korrelation.
Simulation unterschiedlicher Gruppenbildungsarten
Nach der Aufarbeitung der verschiedenen Arten, den Zusammenhang zwischen einer x und y-Variablen auf zwei
unterschiedlichen Ebenen zu operationalisieren, soll die ursprüngliche Fragestellung für zwei Ebenen
beantwortet werden, inwiefern der Zusammenhang zwischen zwei Variablen bei Aggregation steigt. Da bei
natürlich entstehenden Gruppen sehr viele sich überlagernde Aspekte bei der Gruppenbildung beteiligt sein
können, ist eine Analyse natürlicher Gruppierungen unergiebig. Um die Effekte unterschiedlicher Arten der
Gruppierung besser verstehen zu können, hat BLALOCK(1964) diverse Gruppierungsverfahren vorgeschlagen.
Drei davon sind die Zufallsgruppierung, die mit x korrelierende und die mit y korrelierende Gruppierung.
Diese Vorgehensweise ist nicht nur theoretisch interessant, auch reale Gruppenbildungsprozesse folgen implizit
solchen Mustern etwa bei der Einteilung von Schülern in Leistungsgruppen oder Sportlern in Trainingsgruppen
usw. Daher ist eine solche Betrachtung der Konsequenzen solch unterschiedlicher Gruppierungsprozesse auch
aus praxisorientierter Sichtweise erstrebenswert.
Die verschiedenen Arten werden hier für einen zufallsgenerierten Datensatz demonstriert. Die anfangs erzeugten
x-y-Werte werden anschließend unterschiedlich gruppiert. Daher bleibt der ‚Total’-Zusammenhang zwischen x
und y für alle Gruppierungsarten gleich; nur die Within- und Between-Komponenten unterscheiden sich bei den
unterschiedlichen Gruppierungen.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 7
Datengenerierung (n=1000)
Die x-Werte sind standardnormalverteilte
Zufallszahlen. Die y-Werte wurden nach der
Gleichung
y = 0.5 x + e
erzeugt, wobei die e-Werte wiederum
standardnormalverteilte Werte sind.
Die Schätzung des Regressionsgleichung reproduziert
die Populationsparameter annähernd.
Die geschätzten Regressionskoeffizienten des TotalModells sind â T = 0.07 und b̂ T = 0.453 (0.034).
Der Determinationskoeffizient 2. Art r2 beträgt: 0.15.
Bei jeder Gruppierung werden die Determinationskoeffizienten 1. Art (für x und y) berechnet, damit die durch
die Gruppenbildung entstehende Between-Variation beurteilt werden kann; zusätzlich werden die RegressionsKoeffizienten des auf der Aggregatsebene berechnet.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 8
Zufalls-Gruppierung
Die Gruppen werden mit Hilfe eines Zufallsgenerators
gebildet. Die standardnormalverteilten Werte werden
gruppiert (bis -2, bis –1.5, bis –1, ... , bis 2, ab 2 ).
 2y|G =0.0055,  2x|G =0.004.
Within-Modell: b̂ w = 0.452, r2 = 0.15.
Modell für Prädiktion von y mit Hilfe der x-Mittelwerte:
b̂ yx j = 0.559, r2 = 0.0009.
Ebene 2-Modell:
b̂ b = 0.559,
r2 = 0.17.
Bei der Zufallsgruppierung sind nahe bei null liegende Determinationskoeffizienten 1. Art (sowohl  2y|G wie
auch  2x|G ) zu erwarten, wie das hier zumindest der Fall ist. Jede Gruppe hat ein ‚Einzugsgebiet’, das jeweils
die gesamte Punktwolke umfasst. Die so entstandenen sehr stark überlappenden Gruppen haben Mittelwerte, die
eng beieinander liegen.
Nach der Formel b̂ T  b̂ b  2x|G  b̂ w (1   2x|G ) muss bei dem sehr kleinen  2x|G =0.004 die Total-Steigung
b̂ T (=0.453) im wesentlichen mit der Within-Steigung übereinstimmen = 0.559 * 0.004 + 0.452 * 0.996.
Gruppierung nach x
Die Gruppen werden auf Grund von x gebildet (bis -2,
bis –1.5, bis –1, ... , bis 2, ab 2 ).
 2y|G =0.153 ,  2x|G =0.966.
Within-Modell: b̂ w = 0.38, r2 = 0.146.
Modell für Prädiktion von y mit Hilfe der x-Mittelwerte:
b̂ yx j = 0.455, r2 = 0.146.
Ebene 2-Modell:
b̂ b = 0.455,
r2 = 0.952.
Bei der Gruppierung nach x muss der Determinationskoeffizient 1. Art für x sehr hoch sein (  2x|G ); jener für y
(  2y|G ) ist nur insofern erhöht als von vornherein ein Zusammenhang zwischen x und y existiert. Jede Gruppe
hat nun ein durch x-Streifen definiertes nicht überlappendes ‚Einzugsgebiet’.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 9
Nach der Formel b̂ T  b̂ b  2x|G  b̂ w (1   2x|G ) muss bei dem sehr hohen  2x|G =0.966 die Total-Steigung
b̂ T (=0.453) im Wesentlichen mit der Between-Steigung übereinstimmen = 0.455 * 0.966 + 0.38 * 0.034.
Gruppierung nach y
Die Gruppen werden auf Grund von y gebildet (bis -2,
bis –1.5, bis –1, ... , bis 2, ab 2 ).
 2y|G =0.97,  2x|G =0.15.
Within-Modell: b̂ w = 0.017, r2 = 0.927.
Modell für Prädiktion von y mit Hilfe der x-Mittelwerte:
b̂ yx j = 2.9, r2 = 0.927.
Ebene 2-Modell:
b̂ b = 2.9,
r2 = 0.952.
Hier weicht die Between-Steigung sehr stark von der Totalsteigung ab, während sie bei den beiden anderen
Gruppierungsarten in der Nähe der Totalsteigung lag.
Da hier aber nur eine einzige Stichprobe gezogen wurde, die unterschiedlich gruppiert wird, können keine
soliden Aussagen über das Verhalten der Schätzer gemacht werden, daher werden im nächsten Abschnitt
wiederholt solche Stichproben gezogen und unterschiedlich gruppiert.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 10
Zusammenhang auf mehreren Ebenen
Die für zwei Ebenen entwickelten Konzepte des Zusammenhangs sollen nun für mehrere Aggregationsebenen
betrachtet werden. Dabei kann nun nicht mehr nur der Total- vom Between-Zusammenhang unterschieden
werden; der Total-Zusammenhang ist der Zusammenhang der beiden Variablen auf der ersten Stufe. Der
Between-Zusammenhang tritt aber mehrfach (auf jeder Aggregationsstufe) auf. Daher wird hier nur vom
Zusammenhang zwischen den Variablen auf den unterschiedlichen Stufen gesprochen. Die erste Stufe enthält
nichtaggregierte Werte, in den höheren Stufen werden jeweils die entsprechenden Mittelwerte betrachtet.
Datengenerierung
Es wird angenommen, dass die Werte als Prozess auf der ersten Ebene
entstehen im Rahmen eines linearen Modells mit folgenden vereinfachenden
Annahmen:
2

x ~ N(0,  x )
y  a  bx  e, 
, Cov ( x, e)  0 . Alle x- und e- Werte werden
2

 e ~ N(0,  e )
unabhängig voneinander aus einer zentrierten Normalverteilung gezogen.
Die Werte auf den höheren Ebenen werden durch Mittelung erzeugt.
ej
yj
Between
2.Ebene
xj
eij
yij
ayx
Total
byx
Trotzdem können auf den höheren Ebenen Zusammenhänge (Regressionen,
xij
1.Ebene
Kreuzprodukte und Korrelationen) berechnet werden. Dabei soll geklärt
werden, welche Konsequenzen für die Maßzahlen auf den höheren Ebenen zu
erwarten sind. Konstitutiv für die Datengenerierung ist aber die erste Ebene; zentral ist dann die Frage, inwiefern
auf Grund der Maßzahlen auf einer höheren Ebene Rückschlüsse auf die erste Ebene möglich sind.
Gruppierung
 Die Gruppen auf den höheren Ebenen werden so gebildet, dass alle Gruppen auf einer Ebene gleich groß
sind.
 Die Art der Gruppenbildung hat gravierend unterschiedliche Konsequenzen für die
Zusammenhangsmaßzahlen, wie im vorigen Abschnitt festgestellt werden konnte. Daher werden auch hier
die drei verschiedenen Arten der Gruppenbildung (Zufallsgruppierung, Gruppierung nach x und die
Gruppierung nach y) betrachtet.
Maßzahlen auf der 1. Ebene
Einige Maßzahlen des Zusammenhangs sollen hier für die Vergleiche zusammengestellt werden; auf der ersten
Ebene sind sie für alle Gruppierungsarten gleich; dabei soll die Populationsgröße (bzw. der Erwartungswert der
Zufallsvariablen) dargestellt werden, nicht nur ein einzelnes Simulationsergebnis. Für die Berechnung der
Varianz der Schätzer muss die Größe der Stichprobe(=n) auf der ersten Ebene bekannt sein.
2
Die Varianz der Störgröße Var(e) =  e2 .
Beispiel: Im Beispiel sei Var(e) =  e = 1, die Varianz von
Die Varianz von x ist Var(x) =  2x .
Die Steigung ist eine Konstante = b.
Die Varianz von y ist gleich Var(y) = b
x sei ebenfalls gleich 1: Var(x)
=  2x = 1.
Die Steigung sei gleich 0.5.
2
 2x
  e2 .
Kovarianz von x und y : Cov(x, y) = Cov(x, a+bx+e) =
Korrelation zwischen x und y: r =Korr(x,y) =
b 2x
b x
b 2  2x   e2
Die Varianz der geschätzten Steigung auf Ebene 1 ist
 e2
 e2
Var( b̂ ) =
=
CP xx
nVar ( x )
.
Die Varianz von y ist gleich Var(y) = 1.25.
Kovarianz von x und y : Cov(x,y) = 0.5
Korrelation zwischen x und y: r =Korr(x,y)
r2 = 0.2
= 0.4472.
Beispiel: Sei n = 1000. Die Varianz des Schätzers von b ist
dann hier Var( b̂ ) =
 e2
1000  2x
= 0.001.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 11
Aggregation
Für die beiden Variablen x und y werden die Mittelwerte gebildet; die Störgrößen sind zwar in Realsituationen
nicht beobachtbar, die Mittelwertbildung erstreckt sich implizit auch auf sie. In den Simulationen sind die
Störgrößen bekannt und können in die Analyse mit einbezogen werden.
Für die folgenden Untersuchungen wird vorausgesetzt, dass alle Gruppen gleich groß sind (= I) bei J Gruppen
mit n = IJ.
Regressionskoeffizienten und Korrelationen
Bei Zufallsgruppierung
Bei der Zufallsgruppierung ist die YULE & KENDALL’sche
Korrelationsinflationsthese scheinbar zutreffend. Im
Schnitt über alle Simulationsreplikation (das entspricht dem
Erwartungswert) sind die Korrelationskoeffizienten etwa
gleich für die Aggregationsebenen, die mindestens 10
Gruppen umfassen; bei sehr wenigen Gruppen (mit großen
Gruppengrößen) steigt er an. Das ist allerdings nur ein
Schätzproblem: der Korrelationskoeffizientenschätzer ist nur
approximativ (Gruppenanzahl  ) erwartungstreu. Die
Populationskorrelationen bleiben gleich. Daher ist die
Korrelationsinflationsthese hier falsch.
Im Schnitt über alle Simulationsreplikationsstichproben sind
die Steigungen gleich für alle Aggregationsebenen. Diese
Aussage über die Steigung entspricht dem Satz über die
Erwartungstreue der geschätzten Regressionskoeffizienten,
nämlich dass der Erwartungswert der Steigung auf höherem
Aggregationsniveau gleich der Populationssteigung ist.
Der Standardfehler der geschätzten Steigung ist auf hohen
Aggregationsebenen (Gruppenanzahl klein bzw.
Gruppengröße groß) wesentlich größer als bei niedrigen
Ebenen.
Die Gesamtheit auf der 1. Stufe sei n = 1000. Die Graphik
zeigt die Varianzen von x und y plus die Kovarianz zwischen
x und y.
Die Achse unten gibt an, in wie viele Gruppen(=J) die 1000
Fälle eingeteilt werden. Die Gruppengröße ist I = 1000/ J.
b
r2
Std( b̂ )
Gruppenanzahl
Die Verbindungslinien haben nur den Zweck, die
Zusammengehörigkeit der Punkte zu zeigen. Die
Berechnungen wurden für folgende Gruppenanzahlen
durchgeführt: 4, 5, 10, 20, 40, 50, 100, 200 und 500.
Bei Gruppierung nach x
Bei der Gruppierung nach x werden die Gruppen so gebildet, dass alle Gruppen gleich groß werden, oder anders
ausgedrückt, die Verteilung der x-Werte wurde in gleich große Anteile eingeteilt. Bei J Gruppen sollen, ist der
Anteil pro Gruppe 1/J. Die Grenzen der Gruppen sind die x-Quantile zu den Quanten 1/J, 2/J usw.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 12
Die Korrelationsinflationsthese ist hier richtig. Die
Korrelationskoeffizienten werden mit zunehmender
Aggregation größer.
Gruppierung nach x
r2
Im Schnitt über alle Simulationsreplikationsstichproben sind
die Steigungen gleich für alle Aggregationsebenen. Dies
entspricht der Behauptung, dass der Erwartungswert der
Steigung auf höherem Aggregationsniveau gleich der
Populationssteigung ist.
b
10 Std( b̂ )
Der Standardfehler der geschätzten Steigung ist auf hohen
Aggregationsebenen etwas größer (aber nur geringfügig) als
bei niedrigen Ebenen. Insgesamt ist der Standardfehler sehr
klein im Vergleich zur Zufallsgruppierung. Damit er
überhaupt in der Graphik sichtbar wird, wurde er zudem mit
10 multipliziert.
Gruppenanzahl
Die Berechnungen wurden für folgende Gruppenanzahlen
durchgeführt: 2, 4, 5, 10, 20, 40, 50, 100, 200 und 500.
Bei Gruppierung nach y
Die Korrelationskoeffizienteninflation schlägt hier
wiederum voll zu.
Gruppierung nach y
Der Standardfehler der geschätzten steigt hier ebenfalls
stärker (als bei der Gruppierung nach x) . Insgesamt scheint
der Standardfehler klein zu sein im Vergleich zur
Zufallsgruppierung (allerdings wird er stark unterschätzt, wie
im Vertiefungsabschnitt zu berichten sein wird).
r2
Problem: Die Steigungen sind nicht gleich für alle
Aggregationsebenen. Dies widerspricht der Behauptung,
dass der Erwartungswert der Steigung auf höherem
Aggregationsniveau gleich der Populationssteigung ist. Hier
ist offensichtlich eine Voraussetzung des Satzes verletzt, was
zu untersuchen ist.
Bei großen Gruppen tendiert die Steigung b gegen
Var ( y )
Cov ( x , y )
b
10 Std( b̂ )
Gruppenanzahl
Die Berechnungen wurden für folgende Gruppenanzahlen
durchgeführt: 2, 4, 5, 10, 20, 40, 50, 100, 200 und 500.
(das ist sogar der Kehrwert der zu erwartenden Formel!)
Kreuzprodukte der Mittelwerte
Die Basis der Berechnung der Regressionskoeffizienten, Standardfehler und Korrelationen sind die Varianzen
und Kovarianzen der Mittelwerte auf dem entsprechenden Aggregationsniveau.
Die Varianzen bzw. Kovarianzen der Mittelwerte können als Between-Kreuzprodukte dargestellt werden.
Bei Zufallsgruppierung
Bei der Zufallsgruppierung sind die gemittelten Variablen über die Fälle hinweg ebenfalls unabhängig. Daher
können die Varianzen und Kovarianzen der Mittelwerte der Variablen (=y(I), x(I), e(I)) über die jeweiligen I
Zufallsvariablen der Einheiten einer Gruppe auch sehr einfach theoretisch berechnet werden (die Varianz eines
Mittelwerts von unabhängigen Zufallsvariablen ist gleich der Populationsvarianz durch die Anzahl, über die
gemittelt wird; das gilt auch für die Kovarianzen); zusammengestellt in einer Matrix:
 y ( I) 
Var  x (I) =
 e(I) 
1
I
Var ( y)
1
Cov ( x, y)
I
1
Cov (e, y)
I
1
I
Cov ( y, x )
1
Var ( x )
I
1
Cov
(e, x )
I
1
Cov ( y, e)
I
1
Cov ( x, e)
I
1
Var (e)
I
1
I
=
b  xx   
2
1
I
2
e
b  xx
1 2

I e
1
b  xx
I
1

I xx
0
 e2
0 ,
1 2

I e
1
I
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 13
wobei die Varianzen und Kovarianzen Var(y), Cov(y,x) usw. denjenigen der Population entsprechen; zusätzlich
kann die Generierung der Daten durch das lineare Modell berücksichtigt werden, sodass die Varianzen und
Kovarianzen jeweils auf die Varianz von x (  xx bzw.  2x ), die Varianz der Störgröße (  e2 ) und den
Regressionskoeffizienten b zurückgeführt werden können.
Andererseits müssen die Varianzen (bzw. Kovarianzen) in einer Stichprobe geschätzt werden. Als Basis zur
Entwicklung eines Schätzers können die Between Kreuzprodukte CP xx , B , CPxy ,B usw. verwendet werden.
Erwartungstreue Schätzer erhält man etwa nach der Momentenmethode folgendermaßen. Der Erwartungswert
des Kreuzprodukts unter Unabhängigkeit der Beobachtungen ist E( CPxy ,B ) = (J-1) Cov(x,y). Daher wird die
Kovarianz erwartungstreu geschätzt durch
geschätzt werden durch Cov ( x(I), y(I)) 
CPx y, B
J 1
CP xy ,B
I(J  1)
. Die Kovarianz der Mittelwerte kann daher erwartungstreu
=
CP xy , B
IJ  I
Für die vorliegende Simulation ist die Varianz-Kovarianz y ( I) 
1.25 0.5 1
matrix gleich Var  x (I) = 1I 0.5 1 0 .


1
0 1
 e(I) 
. Entsprechend für die anderen Kreuzprodukte.
Zufalls-Gruppierung
Var(y)
Das Mittel (entspricht dem Erwartungswert) über die
Simulationsreplikationen der geschätzten Varianzen und
Kovarianzen der Mittelwerte steigen linear mit der
J
1.25 ,
Gruppenanzahl (z.B. Var(y(I))= 1I 1.25 = 1000
Cov(x(I),y(I))=
J
0.5
1000
Konsequenz etwa für den Regressionskoeffizienten:
Cov( x ( I ), y ( I ))
Var ( x ( I ))
=
Cov(x,y)
).
Denn J = 1000/I (J ist die Gruppenanzahl, I ist die
Gruppengröße). Die Variation aller Variablen schrumpft bei
zunehmender Gruppengröße proportional.
b
Var(x)
Cov ( x , y )
Var ( x )
Gruppenanzahl
Die Berechnungen wurden für folgende Gruppenanzahlen
durchgeführt: 4, 5, 10, 20, 40, 50, 100, 200 und 500; als
Vergleich zusätzlich für 1000 ‚Gruppen’
, da sich I wegkürzt.
Bei Gruppierung nach x
Bei der Gruppierung nach x werden die Gruppen wiederum so gebildet, dass alle Gruppen gleich groß werden,
oder anders ausgedrückt, die Verteilung der x-Werte wurde in gleich große Anteile eingeteilt. Bei J Gruppen
sollen, ist der Anteil pro Gruppe 1/J. Die Grenzen der Gruppen sind die x-Quantile zu den Quanten 1/J, 2/J usw.
J ist die Gruppenanzahl.
Die erwartungstreue Schätzung der Varianzen und Kovarianzen kann bei der Zufallsgruppierung mit Hilfe der
Division der Kreuzprodukte durch n-I bzw. durch IJ-I bei gewichteten Kreuzprodukten (bzw. Division durch J-1
bei ungewichteten Kreuzprodukten) erreicht werden. Bei der Gruppierung nach x (ebenfalls bei der nach y) hilft
dieser einfache Trick nicht. Der Erwartungswert mancher Kreuzprodukte auf einem bestimmten Aggregationsniveau ist anders als bei der Zufallsgruppierung, z.B. für das von x mit x: E(CPxx .B )  IJVar(x(I))   2x ,
daher ist der erwartungstreue Schätzer für die Varianz des Mittelwerts über die I Beobachtungen aus einer
Gruppe: V̂ar(x(I))  CPxx .B / IJ   2x / IJ ; d. h. für die erwartungstreue Schätzung der Varianz des Mittelwerts
muss entweder  2x (die Varianz des x-Variable) bekannt sein oder andersweitig geschätzt werden. Bei großem n
ˆ e2  CPee.B /(IJ  I) der erwartungstreue
(=IJ) wird  2x / IJ sehr klein. Für die Varianz von e wäre weiterhin 
Schätzer. Dieser Umstand wird im Vertiefungsabschnitt näher behandelt. Für die vorliegende Simulation wurden
alle Schätzer auf der Basis der Division der Kreuzprodukte durch IJ gebildet.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Die formelmäßige Beschreibung ist hier wesentlich
komplizierter(siehe Vertiefungsabschnitt). Es kann aber
folgendes festgehalten werden:
Auch hier steigen die Varianz von y und jene von e linear
mit der Gruppenanzahl.
Völlig anders verhalten sich die Varianz von x und die
Kovarianz von x mit y. Sie bleiben nahezu gleich; hier bleibt
ja die x-Variationsbreite in etwa erhalten.
Konsequenz: Da sich die Kovarianz zwischen x und y
ähnlich wie die Varianz von x verhält (=Steigung), bleibt das
Verhältnis der beiden in etwa konstant.
Bei der Korrelation wird aber die konstante Kovarianz
sowohl durch die Standardabweichung von x und durch die
von y dividiert, daher nimmt die Korrelation bei kleiner
werdender Gruppenanzahl zu.
Seite 14
Gruppierung nach x
Var(x)
Cov(x,y)
Var(y)
Var(e)
Gruppenanzahl
Die Berechnungen wurden für folgende Gruppenanzahlen
durchgeführt: 2, 4, 5, 10, 20, 40, 50, 100, 200 und 500.
Bei Gruppierung nach y
Auf den ersten Blick ist das Bild harmlos: gegenüber der xGruppierung ist die Rolle von x und y vertauscht.
Auch hier steigt die Varianz von x linear mit der
Gruppenanzahl, die von y bleibt konstant. Die lineare
Steigung der Varianz von e mit der Gruppenanzahl ist hier
gedämpft.
Gruppierung nach y
Var(y)
Var(e)
Die Kovarianz von x mit y bleibt ebenfalls gleich; hier bleibt
ja die x-Variationsbreite in etwa erhalten.
Konsequenz: Da sich jetzt die Kovarianz zwischen x und y
anders als die Varianz von x verhält (=Steigung), bleibt das
Verhältnis der beiden in nicht konstant; deswegen verändert
sich die Steigung im Widerspruch zum Satz zur
Erwartungstreue des aggregierten Schätzers.
Cov(x,y)
Var(x)
Gruppenanzahl
Die Berechnungen wurden für folgende Gruppenanzahlen
durchgeführt: 2, 4, 5, 10, 20, 40, 50, 100, 200 und 500.
Der Widerspruch zum Satz zur Erwartungstreue des aggregierten Schätzers soll genauer untersucht werden. Die
Modellvoraussetzung bei der Datengenerierung ist bei der vorliegenden Simulationsstudie gewährleistet. Daher
muß eine andere Voraussetzung des Satzes verletzt sein. Bei dieser genaueren Untersuchung werden aber auch
weitere Probleme deutlich werden.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 15
Zusätzlich zu den Varianzen von x und y und deren
Kovarianz werden hier die Kovarianzen der Variablen mit e
betrachtet.
Gruppierung nach y
Var(y)
Besonders störend ist dabei, dass die Kovarianz zwischen e
und x bei Aggregtion nicht null bleibt. Das ist exakt der
Grund für den besagten Widerspruch zum Satz zur
Erwartungstreue des aggregierten Schätzers, bei dem
vorausgestzt wird, dass diese Kovarianz null ist. Das Nullsein
dieser Kovarianz ist zusätzlich eine zentrale Forderung bei
der OLS- und GLS-Schätzung.
Daher ist weiter auch nicht verwunderlich, dass die Varianz
von e hier überhaupt nicht mehr mit Hilfe der Varianz der
Residuen geschätzt werden kann: siehe dazu den völlig
unterschiedlichen Verlauf der Kurven für Var(e) und
Var(res).
Cov(e,y)
Var(e)
Var(res)
Cov(x,y)
Var(x)
Cov(e,x)
Gruppenanzahl
Es sei hier darauf hingewiesen, dass bei der Gruppierung nach Zufall und nach x die Kovarianz zwischen e und x
jeweils 0 bleibt und die Varianz von e jeweils erwartungstreu durch die Varianz der Residuen geschätzt werden
kann.
Theoretische Behandlung der Gruppierung nach x (bzw. y)
Bei beiden Gruppierungsarten ist die theoretische Behandlung der Korrelationen, Steigung und der diversen
Kreuzprodukte etwas komplizierter als im Zufallsgruppierungsfall. Hier muss für eine adäquate Behandlung der
Kreuzprodukte berücksichtigt werden, dass die Werte zwecks Gruppierung sortiert werden (nach x bzw. y); das
hat die Konsequenz, dass die zu betrachtenden Variablen nicht mehr unabhängige Zufallsgrößen sind, sondern
geordnete Werte. Die Zufallsgrößen müssen nach der Sortierung als Ordnungsstatistiken (sortierte Liste)
behandelt werden. Die Ordnungsstatistiken sind dann der Ausgangspunkt der theoretischen Herleitung der
Kreuzprodukte und der Schätzer (siehe Vertiefungsabschnitt). Da die Behandlung mit Hilfe von
Ordnungsstatistiken relativ kompliziert ist, wird zudem im Vertiefungsabschnitt gezeigt, dass eine Annäherung
durch ein Modell mit den Quantilen als festen Gruppengrenzen recht gut gelingt; dieses Modell ähnelt einer
Varianzanalyse mit einem fixen Faktor.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 16
Vertiefungsabschnitt:
Varianzen der Mittelwerte der Ordnungsstatistiken
Wenn die Daten sortiert werden und auf der Basis der sortierten Werte die Gruppen gebildet werden, sind die zu
betrachtenden Zufallsvariablen nicht mehr die ursprünglichen unabhängigen Variablen, sondern die Ordnungsstatistiken (engl. Order statistics, auch Positionsstatistiken genannt (siehe Fisz(1973)).
So kann auf der Basis der n Ordnungsstatistiken auch die Varianz der Zufallsvariablen x selbst betrachtet
werden. Dabei ist zu berücksichtigen, dass hier eine Mischung der Verteilung der n Ordnungsstatistiken vorliegt.
Die Wahrscheinlichkeit, einen x-Wert bestimmter Größe zu realisieren, kann zweistufig berechnet werden,
einerseits wird mit der Wahrscheinlichkeit 1/n eine der Ordnungsstatistikverteilungen ausgewählt, danach
innerhalb dieser Verteilung der Wert realisiert. Im Folgenden wird vorausgesetzt, n = I*J ist. Die Abkürzung der
Ordnungsstatistiken folgt der üblichen Konvention, die Indizes in Klammern zu setzen. Wegen der
Gruppierungen werden i.a. Doppelindizes verwendet, wobei die übergeordnete Sortierung der j-Index ist,
innerhalb dessen die Werte wiederum sortiert sind und mit i indiziert sind.
Varianz der Zufallsvariablen x:  xx   2x  Var(x) = IJ1  j1  1 Var ( x j )  IJ1  j1  1 E( j  ) 2
J
 j1 1 E(x j  ) 2
J
Denn: Var(X) = 1
IJ
I
= 1
IJ
I
J
I
 j1 1 E(( x j   j )  (   j )) 2
J
I
E(( x j   j )  (   j )) 2 = E(x j   j ) 2  2E(x j   j )(   j )  E(   j ) 2 =
E( x j   j ) 2  E(   j ) 2 .
 j1 1 E(x j   j ) 2  IJ1  j1 1 E( j  ) 2 =
J
I
J
I
1
Var ( x j )  IJ1  j1  1 E( j  ) 2 . Qed.
IJ  j1  1
J
1
Daher: Var(X) = IJ
I
J
I
Varianz der Zufallsvariablen des Mittelwerts , gemittelt über jeweils alle I Zufallsvariablen jeweils einer
 j1 ,i Cov (x j , x ij )  1J  j1 (Ex  j  Ex ) 2 , wobei Ex ( ) der Erwartungswert
I
der Zufallsvariablen x ist und Ex  j =(=   j ) = E 1I iI x ij = 1I i Ex ij ist.
J
I
J
I
I
Denn: Var ( x (I)) = Var ( 1  x i ) = 1J E ( 1I 
x  ) 2  = 12  j1 E( 1 ( x j  )) 2 =
j1
 1 j
I
i 1
JI
Gruppe: Var ( x (I)) =
J
1
JI 2
I, I
J
1
JI 2
 j1 E( 1 (( x j   j )  ( j  )) 2
1
JI 2
 j1  1 i 1 E((( x j   j )  ( j  ))(( x ij   ij )  ( ij  ))) =
J
I
J
I
=
I
[es gilt: E(((x j   j )  ( j  ))((x ij   ij )  ( ij  ))) =
(wegen ( j  )E(x ij   ij )  E(x j   j )( ij  )  0 )
E(((x j   j )(x ij   ij )  ( j  )( ij  ))) ] =
1
JI 2
 j1  1 i 1 E((( x j   j )( x ij   ij )  ( j  )( ij  ))) =
1
JI 2
 j1 ,i Cov (x j , x ij )  1J  j1 (  j  ) 2 . Qed.
J
I
J
I
I, I
J
Die Kovarianz der Mittelwerte über jeweils alle I Zufallsvariablen jeder Gruppe x ( I) und y(I) ist
Cov ( x(I), y(I)) =
1
JI 2
 j1 ,i Cov (x j , y ij )  1J  j1 (Ex  j  Ex )( Ey  j  Ey ) , wobei
J
I, I
J
Ex bzw. Ey der
Erwartungswert der Zufallsvariablen x bzw. y sind; entsprechend sind auch Ex  j bzw. Ey  j .definiert.
Problem bei Ordnungsstatistiken: Die Ordnungsstatistiken sind nur asymptotisch erwartungstreu für die
entsprechenden Quantile; sie konvergieren besser, wenn die entsprechenden Quanten nicht exakt i/n gewählt
werden, sondern i/(n+k) mit k=0.20. Zudem ist zu gewährleisten, dass die Quantile symmetrisch angelegt
werden, d.h. a  n 1 k  1  a  n n k mit a als Verschiebungskonstante. Daraus folgt auch die Größe der


Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 17
Verschiebungskonstante: a  0.5 nk1k . Das i. Quantum ist daher q i 
i  0.5(1 k )
nk
. Die Ordnungsstatistiken
x (i ) und x ( j) einer Stichprobe der Größe n sind approximativ (n) normalverteilt mit den Mittelwerten
E(x (i) )  quantil(q i ) , E(x ( j) )  quantil(q j ) und Varianzen Var ( x (i ) ) 
Die Kovarianz ist gleich Cov ( x (i ) , x ( j) ) 
q i (1  q j )
q i (1  q i )
nf i2
, Var ( x ( j) ) 
q j (1  q j )
nf j2
.
für i<j, wobei f i  f (quantil(q i )) und f(x) die
nf i f j
Dichtefunktion der originären x-Werte ist bzw f i  f (quantil(q i )) (siehe FISZ(1973), S.479). Die Kovarianz für
alle i und j lautet Cov ( x (i ) , x ( j) ) 
q min( i, j)  q i q j
nf i f j
.
Hilfssatz: Die Varianz der originären ursprünglich unabhängig voneinander gezogenen x-Werte xx ist gleich
der Summe aller Varianzen und Kovarianzen der Ordnungsstatistiken:  xx 
1
IJ
 j, k,g Cov (x j , x kg ) . Die
J,I
I, J
Varianz ist im übrigen gleich der Summe aller Varianzen und Kovarianzen von irgendwie auch immer
veränderter Reihenfolge der ursprünglichen Zufallsvariablen.
Denn: Da die Summe von Variablen gleich groß ist für jede Vertauschung der Summanden (nach dem Kommutativgesetz), ist
auch die Varianz einer Summe von Zufallsvariablen
Var ( j, x j ) ist gleich groß für jede Vertauschung; speziell gilt das
J,I
für die ursprünglich unabhängig voneinander gezogene Reihenfolge, dh.
Zudem gilt allgemein für die Varianz der Summe
Var ( j, x j ) =
J,I
Var ( j, x j ) = Var (iJ*I x i ) = JI xx .
J,I
 j, k,g Cov (x j , x kg ) . Nach Division durch
J,I
I, J
JI folgt die Behauptung. Qed.
Varianzen und Kovarianzen der Mittelwerte linearer Funktionen
Sei y eine lineare Funktion von x und e. Das datengenerierende Modell sei
y = a + b x + e,
wobei x und e stochastisch unabhängig seien. Die Kovarianz zwischen x und e = Cov(x,e) ist daher 0. Die
Kovarianz zwischen x und y ist Cov(x,y)=bVar(x) und die Kovarianz zwischen y und e ist Cov(y,e)=Var(e).
Bei Sortierung nach x
Die Mittelwerte für x sind die Mittelwerte der Ordnungsstatistiken x(I)  1I i x (ij) , die Mittelwerte der
I
mitsortierten Werte sind y(I)  1I i y ij , e(I)  1I i e ij . e(I) selbst besteht aus unabhängig variierenden
I
I
Komponenten, die auch bei Sortierung nach x unabhängig bleiben, während bei der Berechnung von y(I) die
lineare Funktion berücksichtigt werden muss: y(I)  a  b 1I i x (ij)  1I i e ij = a  bx(I)  e(I) , in
I
I
Matrixschreibweise kann die einfache Abhängigkeit übersichtlich geschrieben werden als
b 1
y ( I)
a
x ( I)
.
m(I)  a  Km 0 (I) , mit m(I)  x ( I) , a  0 , K  1 0 und m 0 (I) 
e( I)
0 1
e( I)
0
Die Kovarianzen zwischen x und e sind alle null, daher auch die zwischen den Mittelwerten, daher ist die
Var ( x (I))
0
Varianz-Kovarianzmatrix von m 0 (I) gleich Var( m 0 (I) ) =
. Die Varianz von x(I) ist die
0
Var (e(I))
Varianz der Mittelwerte von Ordnungsstatistiken
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Var(x(I))=
1
JI 2
Seite 18
 j1 ,i Cov (x j , x ij )  1J  j1 (Ex  j  Ex ) 2 , die Varianz von e(I) ist die Varianz der
J
I, I
J
Mittelwerte von unkorrelierter Zufallsvariablen Var(e(I)= 1I Var (e) =
1
I
 e2 . Die Varianz-Kovarianzmatrix von
m(I) ist daher Var( m(I) ) = KVar (m 0 (I))K  . Die folgenden zwei Ausdrücke sind Elemente dieser VarianzKovarianzmatrix:
Cov ( y(I), x(I)) = Cov (a  bx(I)  e(I), x(I)) = b 2 Var (x(I)) , weil Cov (e(I), x (I)) null ist
Var ( y(I)) = b 2 Var (x(I))  Var (e(I)) , weil Cov (e(I), x (I)) wiederum null ist.
Die Übereinstimmung der
theoretischen
Berechnungen
, die nach den
oben
skizzierten
Prinzipien
erfolgte, mit
den bereits
oben
gezeigten
Simulationen
der Varianzen
und
Kovarianzen,
ist
hervorragend.
Gruppierung nach x (theoretische Berechnung)
Var(x)
Cov(x,y)
Var(y)
Var(e)
Gruppenanzahl
Gruppierung nach x (Simulation)
Var(x)
Cov(x,y)
Var(y)
Var(e)
Gruppenanzahl
Vergleich der theoretischen Berechnungen mit den Simulationen
Bei Sortierung nach y
Falls nach y sortiert wird, wird e und x implizit mitsortiert und zwar in dem Ausmaß, in dem die Variablen
regressionsgemäß von y her prädizierbar sind, d.h.
e  a ey 
Cov ( y,e )
Var ( y )
oder kürzer e  a ey  b ey y  e.y
y  e.y
bzw.
bzw.
x  a xy 
Cov( y, x )
Var ( y )
y  x.y ,
x  a xy  b xy y  x.y , mit b ey 
Cov( y,e )
Var ( y )
und b xy 
Cov( y, x )
Var ( y )
Beide Variablen können in Form einer Regressionsgleichung dargestellt werden bzw. als Summe zweier Teile,
deren erster Teil jeweils der von y her prädizierbare Teil und deren zweiter Teil mit y nicht korreliert (die
Residuen e.y bzw. x.y unter Konstanthaltung von y).
y
a xy
 b xy 1 0
x .y
w= x , a =
In Matrixschreibweise ist r  a  K r w , mit r 
und K r =
.
a

b ey 0 1
e.y
ey
e
Die Varianz-Kovarianzmatrix von r ist Var( r ) = K r Var( w ) K r =
b 2xy Var ( y)  2b xy cov(x, y)  var(x)
b xy b ey Var ( y)  b ey cov(x, y)  b xy cov(e, y)
b xy b ey Var ( y)  b ey cov(x, y)  b xy cov(e, y)
2
b ey
Var ( y)  2b ey cov(e, y)  var(e)
.
Die Elemente dieser Matrix, die beiden Varianzen und die Kovarianz, werden nun noch weiter vereinfacht.
( y,e)
Cov( y, x )
Eigenschaften von e.y bzw. x.y: e.y  e  a ey  Cov
y , x.y  x  a xy  Var ( y) y .
Var ( y )
Var (e.y)  Var (e) 
Cov 2 ( y,e)
= Var (e)
Var ( y)
1 

Var ( e )
,
Var ( y )
Var (x.y)  Var (x) 
Cov (e.y, x.y)  b
Denn: a)
Var (e.y)  Var (e) 
Cov 2 ( y ,e )
Var 2 ( y )
Cov2 ( y, x )

= Var ( x )
Var ( y)

1
b 2 Var ( x ) 
und
Var ( y ) 

Var ( e) Var ( x )
.
Var ( y )
Var ( y)  2Cov (e, y)
Cov ( y ,e )
Cov 2 ( y,e)
= Var (e) 
. Entsprechend für x.y.
Var ( y )
Var ( y)
Nagl, Multilevel-Modelle, Materialien, Anhang A1
b) Da Cov(x,e)=0, gilt

Cov( y,e)
Var ( y )
Cov (e.y, x.y)  Cov (e 
Cov ( y, x ) 
Cov( y, x )
Var ( y )
Cov ( y, e) 
Seite 19
Cov( y,e)
Var ( y )
y, x 
Cov( y, x ) Cov( y,e)
Var ( y ) Var ( y )
Cov( y, x )
Var ( y )
y) =
,e) Cov( y, x )
Var ( e ) bVar ( x )
= 
. Qed.
Var ( y) =  Cov( yVar
( y)
Var ( y )
Wenn die Variablen nach y sortiert werden, werden die andern Variablen implizit mitsortiert. Die Symbole ek
und xk werden hier verwendet, um die k’te Variable in der nach y sortierten Liste zu bezeichnen; wobei y(k)
die k’t größte y-Variable ist; y(k) ist daher die Ordnungsstatistik. Auch die entsprechenden k’ten e-Variablen
und x-Variablen können in die beiden Teile zerlegt werden:
e k  a ey 
Cov ( y, x )
y ( k )  e.y k bzw. x k  a xy  Var ( y) y ( k )  x.y k
Cov( y,e )
Var ( y )
Die Kovarianz zweier Werte x i , e k aus der nach y sortierten Liste ist nicht 0:
Cov ( x i , e k )  Cov (
Cov( y, x ) Cov( y,e )
Var ( y )
Var ( y )
Cov( y, x )
Var ( y )
y (i )  x.y i ,
Cov( y,e)
Var ( y )
y ( k )  e.y k ) =
Cov ( y (i ) , y ( k ) )  Cov ( x.y i , e.y k ) = b xy b ey Cov( y (i) , y (k ) )
Mittelwerte
Die Mittelwerte für y sind die Mittelwerte der Ordnungsstatistiken y(I)  1I i y (ij) , die Mittelwerte der
I
mitsortierten Werte sind x(I)  1I i x ij , e(I)  1I i e ij . Diese wiederum werden nach den obigen
I
Überlegungen zerlegt: x(I)  a xy  b xy
I
1
I
i y (ij)  1I i x.y ij = a xy  b xy y(I)  1I i x.y ij , wobei alle
I
I
I
x.y ij
untereinander unkorreliert und mit y(I) unkorrelierte Zufallsvariablen sind; bzw. x(I)  a xy  b xy y(I)  x.y(I) .
y ( I)
0
Entsprechendes gilt für e: e(I)  a ey  b ey y(I)  e.y(I) ; in Matrixschreibweise: x ( I) = a xy
e( I) a ey
1
+ b xy
b ey
0 0
1 0
0 1
y ( I)
x .y ( I ) .
e.y( I)
Varianzen und Kovarianzen der Mittelwerte


Var ( e )
( y ,e ) 
= VarI(e) 1  Var
Var (e.y(I)) = 1I Var (e.y) = 1I  Var (e)  Cov
( y)
Var ( y ) 


Cov 2 ( y, x )
Var ( x )
b 2 Var ( x )
Var (x.y(I)) = 1I Var (x.y) = 1I  Var ( x )  Var ( y)  = I  1  Var ( y) 




2
Mit Hilfe der Matrixschreibweise kann die Struktur der Kovarianzen und Varianzen übersichtlicher dargestellt
werden. Aus der Varianz-Kovarianz-Matrix der drei Variablen y(I), x.y(I) und e.y(I)
y ( I)
Var ( y(I))
0
0
0
Var ( x.y(I))
Cov (e.y(I), x.y(I))
Var( x.y( I) ) =
0
Cov (e.y(I), x.y(I))
Var (e.y(I))
e.y( I)
kann die Varianz-Kovarianz-Matrix der Mittelwerte y(I), x(I) und e(I) (oben wurden diese Variablen bereits als
Linearkombination von y(I), x.y(I) und e.y(I) dargestellt) berechnet werden. Die Varianz-Kovarianzmatrix
1 0 0
y ( I)
y ( I)
Mittelwerte y(I), x(I) und e(I) sind durch das Matrixprodukt Var x ( I) = b xy
e( I)
b ey
1 b xy
1 0 Var( x.y( I) )
e.y( I)
0 1
b ey
0
1
0
0
0
1
darstellbar. Wegen der speziellen Struktur der Koeffizientenmatrix ist die Kenntnis von
Cov (e.y(I), x.y(I)) nicht erforderlich. Die folgenden Ausdrücke sind die Elemente dieser VarianzKovarianzmatrix:
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Var ( y(I)) =
1
JI 2
Seite 20
 j1 ,i Cov ( y j , y ij )  1J  j1 (Ey  j  Ey ) 2 ,
J
I, I
J

Var ( e )
2
2
Var ( y( I)) + VarI(e) 1  Var
Var (e(I)) = b ey
Var ( y(I))  Var (e.y(I)) = b ey
( y)

Var ( x ) 
Var ( x (I)) = b 2xy Var ( y(I))  Var ( x.y(I)) = b 2xy Var ( y(I)) + VarI( x )  1  bVar
( y) 


2
Cov ( x (I), e(I)) = b xy b ey Var ( y(I))  Cov(x.y(I), e.y(I)) = b xy b ey Var ( y(I))  bI
Var ( e ) Var ( x )
Var ( y )
Cov (x(I), y(I)) = b xy Var ( y(I))  Cov(x.y(I), y(I)) = b xy Var ( y(I))
Cov (e(I), y(I)) = b ey Var ( y(I))  Cov(e.y(I), y(I)) = b ey Var ( y(I)) .
Die Ausdrücke enthalten jeweils die Varianz von y(I), die auch bei größeren Stichproben kaum abnimmt, bzw.
Varianzen der unkorrelierten Zufallsgrößen, die bei steigendem I mit dem Faktor 1/I abnehmen. Besonders
bemerkenswert ist die Kovarianz zwischen x(I) und e(I), sie ist ab I>1 nicht null.
Der Regressionskoeffizient der Mittelwerte
byx(I) =
Cov( y ( I ), x ( I ))
Var ( x ( I ))
=
Cov ( y, x )
Var ( y )
Cov 2 ( y, x )
Var 2 ( y )
Var ( y(I)) 
Var ( x )
I
bVar ( x )Var ( y(I))
b 2 Var 2 ( x )
Var ( y )
Var ( y(I)) 
Var ( x )
I
 Var ( y)  b
Bei zunehmendem I strebt byx(I) gegen
Regressionskoeffizientenschätzers
2
Cov ( y , x )
Var ( y )
Var ( y(I))
 1  b 2 Var ( x ) 

Var ( y ) 


=
Cov 2 ( y , x )
Var 2 ( y )
Var ( y(I)) 
Var ( y(I))
Var ( x )
I
Var ( y(I))
Var ( x )

Var ( y )
bVar ( x )
bzw.
Cov ( x , y )
Var ( y )
=
bVar ( x )
Var ( y )
Var ( y(I))  1I
Var ( y )
Cov ( x , y )

Var ( y )
b
 bVar ( x )



Var ( y )  b 2 Var ( x ) 

Var ( y )
=


(eigenartigerweise sogar der Kehrwert des
).
Vergleich der theoretischen Berechnungen mit den Simulationen
Gruppierung nach y (theoretische Berechnung)
Var(y)
Cov(e,y)
Var(e)
Cov(x,y)
Var(x)
Gruppenanzahl
Cov(e,x)
Die Übereinstimmung der
theoretischen
Berechnungen,
die nach den
hier skizzierten
Prinzipien
erfolgte, mit
den bereits
oben gezeigten
Simulationen
der Varianzen
und
Kovarianzen,
wird durch die
beiden
Diagramme
demonstriert.
Gruppierung nach y (Simulation)
Var(y)
Cov(e,y)
Var(e)
Var(res)
Cov(x,y)
Var(x)
Cov(e,x)
Gruppenanzahl
Die erwartungstreue Schätzung der Varianzen bzw. Kovarianzen
Für die Kreuzprodukte, mit deren Hilfe die Varianzen und Kovarianzen geschätzt werden sollen, werden nundie
Erwartungswerte berechnet. Die Schätzer ergeben sich dann aus den Erwartungswerten nach der
Momentenmethode.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 21
Die Erwartungswerte einiger Kreuzprodukte
Vorerst sollen die Kreuzprodukterwartungswerte von CP xx.T, CPxx.B und CPxx.W berechnet werden unter der
Voraussetzung, dass nach x sortiert wird, daher also Ordnungsstatistiken zu betrachten sind.
Satz: Zusammenfassung; es gilt:
 j, Var (x j )   xx   j,  j     bzw. =  xx (IJ 1)
J,I
J,I
I
J,I
E(CPxx , W ) =  j, Var ( x j )  1I  j, k Cov ( x j , x kj )   j,  j    j 2 .
J
J
I, I
E (CPxx , B ) = I j (  j    ) 2  1I  j k , Cov ( x j , x kj )   xx bzw. = IJ * Var ( x (I))   xx
J,I
E (CPxx ,T ) =
Denn:
J ,I
2
E(CPxx , B )  E(CPxx ,T  CPxx , W ) = E(CPxx ,T )  E(CPxx , W )
  j       j    j 2   xx  1I  j k, Cov (x j , x kj )
J,I 2
J,I 2
J
J
I, I
2
2
=   j  IJ     j   I  j  1   Cov ( x j , x kj )   xx
I
j,
j,
j
j
k ,
J 2
J
I, I
2
1
= I   j  J     Cov ( x j , x kj )   xx . Qed.
I
j
j
k ,
J,I
j,
=
J
2
I, I
Die Behauptungen zu den Erwartungswerten der Total- und der Within-Kreuzprodukte werden in den beiden folgenden Sätzen
Beweisen.
Satz: Der Erwartungswert des Total-Kreuzprodukts ist
 j, Var (x j )   xx   j,  j    
J,I
E (CPxx ,T ) =
Denn:
J ,I
2
E (CPxx ,T ) =  j1  1 E( x j  x  ) 2 =
J
I
..
 j1 1 E(( x j   j )  (x    j )) 2 .
J
I
E(( x j   j )  ( x     j )) 2 = E( x j   j ) 2  2E( x j   j )( x    j )  E( x    j ) 2 =
E( x j   j ) 2  IJ2 g k E( x j   j )( x kg    j ) 
J
I
1
I2J 2
E(g i ( x ig    j )) 2
J
I
g k E(x j   j )( x kg   j ) = IJ2 g k E(x j   j )(( x kg   kg )  ( kg   j )) =
J
I
J
I
2
E( x j   j )( x kg   kg )  IJ2 g k E( x j   j )( kg   j ) =
IJ g k
J
I
(wegen E(x j   j ) =0 ) = 2   Cov ( x j , x kg  ) .
IJ
g
k
J
I
J
I
2
2
b) E(  ( x ig    j )) = E(  (( x ig    ig  )  ( ig    j )) ) =
g
i
g
i
J,I
J,I
g,i f ,t E((( x ig   ig )  ( ig   j ))(( x tf    tf  )  ( tf    j ))) = (weil die Erwartungswerte der
J
a) 2
I
J
I
IJ
Produkte aus Zufallsvariablen und Konstanten 0 werden, werden sie nicht angeschrieben) =
g,i f ,t (E(x ig   ig )( x tf    tf  )  E( ig   j )( tf    j ))
J,I
J,I
=
g,i f ,t Cov(x ig , x tf  )  g,i ( ig   j )
J,I
J,I
2
J,I
Daher gilt wegen a) und b)
E( x j  x  ) 2 =
Var ( x j )  IJ2 k ,g Cov ( x j , x kg  ) 
I, J
1
I J
2 2
g,i f ,t Cov (x ig , x tf  )  I21J 2 g,i ( ig   j )
J,I
J,I
2
J,I
Daher gilt
E (CPxx ,T ) =
 j1 1  Var (x j )  IJ2 k,g Cov (x j , x kg )  I21J 2 g,i f ,t Cov (x ig , x tf  )  I21J 2 g,i ( ig   j )
J
=
=
I
I, J
J,I
J,I
J,I
 j, Var (x j )  IJ1  j, k,g Cov (x j , x kg )   j, I21J 2 g,i ( ig   j )
J,I
J,I
I, J
J,I
2
J,I
 j, Var (x j )  IJ1  j, k,g Cov (x j , x kg )   j,  j    
J,I
J,I
I, J
J,I
2
2



Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 22
Satz: Der Erwartungswert des Within-Kreuzprodukts ist

E(CPxx , W ) =  j, Var ( x j )  1I  j, k Cov ( x j , x kj )   j,  j    j
J,I
J,I
I
J,I
E(CPxx , W ) =  j1  1 E( x j  x  j ) 2 =
J
Denn:
2 .
 j1 1 E(( x j   j )  (x  j   j )) 2
I
J
I
E(( x j   j )  ( x  j   j )) 2 = E( x j   j ) 2  2E( x j   j )( x  j   j )  E( x  j   j ) 2 =
E( x j   j ) 2  2I k E( x j   j )( x kj   j ) 
I
1
I2
E(i ( x ij   j )) 2
I
k E(x j   j )(x kj   j ) = 2I k E(x j   j )((x kj   kj )  ( kj   j )) =
I
I
2
E(x j   j )(x kj   kj )  2I k E(x j   j )( kj   j ) =
I k
I
I
2
E(x j   j )(x kj   kj )  2I E(x j   j )k ( kj   j ) = (wegen E(x j   j ) =0 )
I k
I
I
I
= 2  Cov(x j , x kj )  2 0 ( kj   j ) = 2  Cov( x j , x kj ) .
I
I
I
k
k
k
I
I
I
b) E( ( x ij   j )) 2 =   E((x ij   ij )  ( ij   j ))((x kj   kj )  ( kj   j ))
i
i
k
I
a) 2
I
I
= (wegen
E(x ij   ij )( kj   j )  0 und E( ij   j )(x kj   kj )  0 )
i k E((xij  ij)(xkj  kj)  (ij  j)(kj  j)) =
I
I
I
I
=   E(x ij   ij )(x kj   kj )   ( ij   j ) ( kj   j ) =
i
k
i
k
2
I
I
I
i k Cov ( x ij , x kj )  i ( ij   j ) 
I
=
I
Daher gilt wegen a) und b)
= Var ( x j )  2I
=
=
Hilfssatz:
J
I
I
2
I

I
I
I
2
I
 j1  1 Var (x j )  1I  j1  1 k Cov (x j , x kj )  I12  j1  1 i ( ij   j )
J
I
J
I
I
J
I



2
I
 j1 1 Var (x j )  1I  j1 1 k Cov (x j , x kj )   j1 1  j    j 2 . Qed.
J
I
J
I
I
J
I
 = I  (a  a ) .


  a  Ia     a   2Ia  a  Ia  
 Ia   2I a  a    a  I  a  2I a   I a 


I   a   a   I  a  Ia 
I  a  I a 


 i a i  Ia  
I
I


I
i
2
I 2
 
2

2
I
I

=
I
 j1 1  Var (x j )  2I k Cov (x j , x kj )  I12 i k Cov (x ij , x kj )  I12 i ( ij   j )
Denn:
=
I
E(CPxx , W )
Daher gilt:
=
k Cov (x j , x kj )  I12 i k Cov (x ij , x kj )  I12 i ( ij   j )

= I2  a 2  Ia2
I
2
I
i
I

=

i
I

i
 

2
I
i
I

I 2
1 
I
i
1
I
I
i

i

2
I
2
=
 
I

2
2
2
I
 
=
 
 Ia 
2

i
2
I
2
 1 
2
=
i

2
I 2
 
I
i
2
I
i
i
2
i
2
 , womit die 1. Gleichheit bewiesen ist. Die 2.
Gleichheit entspricht dem üblichen Verschiebungssatz der Varianz

I2  (a   a  )2 = I2  (a 2  2a a  a 2 ) = I2  a 2  2a   a   Ia2 = (wegen der Definition des
I
Mittelwerts als
a   1I 
I
I
a )=
 
I
2

I 2
a
 
2

I
I
. Somit ist auch die 2. Gleichheit bewiesen. Qed.
Vergleich derErwartungswerte der Between Kreuzprodukte
Für die gewichteten Kreuzprodukte gilt:
Satz: Bei Zufallsgruppierung gilt E (CPxx , B ) = (IJ  I) xx ,
bei Gruppierung nach x: E (CPxx , B ) = IJ Var ( x (I))  xx .
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 23
Denn: Das erste Ergebnis ist das Standardergebnis bei der Varianzanalyse. Das Ergebnis bei der Gruppierung nach x ergibt sich
aus dem Erwartungswert
E (CPxx , B ) = I j (  j    ) 2  1I  j k , Cov ( x j , x kj )   xx =
J
J
I, I
 j1 ,i Cov (x j , x ij )  1J  j1 (Ex  j  Ex ) 2 .
J
I, I
J
2
Daher ist IJVar ( x(I)) = 1   Cov ( x j , x ij )  I (Ex  j  Ex ) . Das ist genau der Erwartungswert von
I
j1
 ,i
j1
J
J
I, I
E (CPxx , B ) ohne  xx : E (CPxx , B ) = I j (  j    ) 2  1I  j k , Cov ( x j , x kj )   xx . Qed.
J
Die Varianz des Mittelwerts über I Variable ist Var ( x (I)) = 12
I, I
J
JI
In der Simulation entspricht
 j  I12 E(i (x ij  )) 2
J
I
I
1
I
 j1 i k Cov (x ij , x kj )  1I  j1 i ( ij  )
J
I
I
J
 (x    ) ) =

  x     2I x    I 

= E( 1I Jj
2
I
i
J1
jI
ij
2
J1
jI
I
i
ij
J1
jI
I
i
ij
2
J
j
2
I
i
I
i
ij
2
2
J1
jI
I
i
ij
2
ij
= (bei Simulation gilt:
ij
I
i
dem Ausdruck :
2
I
i
 x    I  = E 


= E   x     2  x    IJ 







E    x      IJ  = E   x      IJ





J

E 1I  j

2
I
2
ij
Mittelwertbildung über die Einzel-Simulationen steht.
2
2

 

  E( IJ1  j i x ij ) ) =
J


I
= E  j Ix 2 j  IJ 2 , wobei E hier für die
J
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 24
Annäherung durch ein Festgrenzen-Modell
Bei der Simulation werden die Werte ohne Beschränkung aus einer Verteilung (Normalverteilung) gezogen und
anschließend gruppiert. Daher ist der Approach über die Ordnungsstatistiken der adäquate. Dabei werden keine
Quantilgrenzen vorgegeben, innerhalb derer die Werte liegen müssen.
Andererseits sind die Erwartungswerte der Ordnungsstatistiken durch die Quantile beschreibbar. Daher ist es
naheliegend, zu untersuchen, ob der Sampleprozess nicht etwa angenähert werden kann durch einen Approach,
bei dem die Quantile selbst von vornherein als feste Grenzen betrachtet werden.
Der Vorteil dieses Ansatzes liegt darin, dass die doch etwas komplizierten Formeln bei den Ordnungsstatistiken
durch einfachere ersetzt werden können. Dabei wird sich zeigen, dass die Annäherung durch ein
Festgrenzenmodell sehr zufriedenstellende Ergebnisse liefern; der Ansatz entspricht einer Varianzanalyse mit
festen Faktoren, wobei allerdings die Varianzen in den Gruppen unterschiedlich groß sind.
Zweistufiger Sample-Approach
Die Berechnung der Varianz für die Gruppierung nach x kann auch ohne Verwendung von Ordnungsstatistiken
durchgeführt werden, indem die Methode der Datengenerierung direkt als zweistufiges Ziehen der Stichprobenwerte interpretiert wird.
Die erste Stufe besteht in der Auswahl einer Gruppe j aus J Gruppen. Die Wahrscheinlichkeit, daß eine bestimmte Gruppe ausgewählt wird, ist gleich 1/J (Gleichwahrscheinlichkeit). Für jede Gruppe wird eine Verteilung
betrachtet, aus der der Wert gezogen wird, daher sind J verschiedenen Zufallsvariablen zu berücksichtigen. Die
Überlegungen werden hier nur für den Spezialfall des Ziehens aus einer normalverteilten Population behandelt.
Da die vorliegende Simulation auf der Normalverteilung
beruht mit den Quantilen als Gruppengrenzen, stellen die
J Verteilungen jeweils die Ausschnitte aus der Normalverteilung zwischen den Quantilen dar mit den J+1
Gruppengrenzen (gj, j=0,..., J). Damit diese Ausschnitte der
Normalverteilung aber selbst Verteilungen darstellen, muss
die Fläche unter der Dichtefunktion gleich 1 sein. Da die
Ausschnitte die Fläche 1/J haben (das Quantum der
Quantile), müssen diese Ausschnitte mit J multipliziert
werden, dann sind das jeweils die entsprechenden bedingten
Verteilungen; für die j. Gruppe ist daher die bedingte
Dichtefunktion gegeben durch:
2

 x  
1

2  
 J
e
für den Bereich x  (g j1 , g j ] .
nd( x )  
 2

0
außerhalb des Bereichs

Der Erwartungswert des Ziehens aus der j. Verteilung ist
gleich E(X j )  (g j1 , g j ] (Kurzbezeichnung  j ), der
Mittelwert der j. Verteilung, oder E(X j )   x (g j1 , g j ] .
Die Varianz Var (X j )  E(X j   x (g j1 , g j ]) 2 =:  2j =
(bzw. etwas ausführlicher abgekürzt) = (  2x (g j1 , g j ] ist die
Varianz der j. Verteilung.
Beispiel: Bei J=4 sind die 5 Quantile der Standardnormalverteilung g0 = -, g1  -0.6745, g2 = 0, g3  0.6745, g4 = .
4*0.3
1 0.492
0.2
0.1
-2
-1
0
1
4*0.3
2
x1
2 0.193
0.2
0.1
-2
-1
0
1
4*0.3
2
x2
3 0.193
0.2
0.1
-2
-1
0
1
4* 0.3
2
x3
4 0.492
0.2
0.1
-2
-1
0
1
2
x4
1  -1.27 2 .325
2  -.325 4  1.27
Die Varianzen der Verteilungen für die 4 Gruppen sind
verschieden groß.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 25
Der Mittelwert für den j. Bereich wird mit Hilfe des Integrals
berechnet: E(X j )   x (g j1 , g j ] =
gj
g j-1 x nd(x) dx =
   2 (nd(g j-1 )  nd(g j )) .
Der Mittelwert für die 1. Gruppe:
E(X1) = 0 + 1 (nd(g0) - nd(g1)) = (0 - 1.27) = -1.27.
Die Varianz Var (X j )  E(X 2j )   x (g j1 , g j ] 2 .
E(X 2j ) ist das Integral
gj
g j-1 x
2
Beispiel: Im Fall der Standardnormalverteilung mit J=4 ist
nd(g0) = 0, nd(g1)  1.27, nd(g2)  1.596, nd(g3)  1.27,
nd(g4) = 0.
Für die Varianz der 1. Gruppe wird zuerst berechnet:
E(X12) = 2 + 2(1+ (g0 +) nd(g0) - (g1 +) nd(g1)) =
= 0 + 1 (1+ (g0 +0) nd(g0) - (g1 +0) nd(g1)) =
= (1+ 0 - (g1+0)(-1.27) = 1.857.
Unter Verwendung von E(X12) ist die Varianz
Var(X1) = 1.8572 – (-1.27)2 = 0.2417. Std(X1) = 0.492
nd(x) dx =
 2   2 (1  (g j-1  ) nd(g j-1 )  (g j  ) nd(g j )) .
Kombination der beiden Stufen
Die gemeinsame Wahrscheinlichkeit etwa für das Ereignis X  x in der j. Gruppe WX  x, G  j = (Produkt der
bedingten und der G-Randwahrscheinlichkeit) =
WX  x | G  j WG  j = W X  x | G  j 1J . Die Randwahrscheinlichkeit
für x WX  x  = WX  x, G  1  X  x, G  2    X  x, G  J  =
1
J
 j1 WX  x, G
J
 j . Entsprechend
kann die Dichtefunktion der Randverteilung berechnet werden, sie ist dann einfach die Normalverteilungsdichte.
Die Zufallsvariable X beschreibt den kombinierten Ergebnisprozess. In der Folge werden die Zufallsvariablen
wieder mit Kleinbuchstaben bezeichnet.
Erwartungswert der Zufallsvariablen x: E( x ) = 1J  j1 E( x j ) =  =: x.
J
Varianz der Zufallsvariablen x:
Var ( x ) = 1J  j1 Var ( x j )  1J  j1 ( x (g j1 , g j ]  ) 2 = E G (Var (x | G))  Var G (E(x | G))
J
Denn:
J
Var ( x ) = (allgemein gilt) = E G (Var (x | G))  Var G (E(x | G)) = (wobei EG bzw. VarG der Erwartungswert
bzw. die Varianz über die Gruppenverteilung bezüglich der bedingten (Bedingungen durch die Ausprägungen der Variablen G)
Var (x | G) bzw. E(x | G) ) =  j1 1J Var ( x j )   j1 1J ( x (g j1 , g j ]  ) 2 . Qed.
J
Größen
J
Beweis alternativ:
Var(X) =
 j1 1J E(x j  ) 2
J
= 1
J
 j1 E(( x j   j )  ( j  )) 2 . Pro Summand gilt: E(( x j   j )  ( j  )) 2
J
=
E( x j   j ) 2  2( j  )E( x j   j )  ( j  ) 2 = E( x j   j ) 2  ( j  ) 2 .
Daher:
Var ( x ) = 1J  j1 E( x j   j )2  1J  j1 ( j  )2 . Qed.
J
J
Zwei Kurzbezeichnungen werden hier eingeführt, damit die Formeln handlicher gestaltet werden können:
 xx := 1J  j1 Var ( x j ) (das ist der Spezialfall bei den vorliegenden Modellannahmen für EG (Var ( x | G)) ).
J
 IC( x ,I) :=
1
J
 j ((g j1 , g j ]  ) 2
(das ist der Spezialfall bei den Modellannahmen für Var G (E( x | G)) ). Die
Bezeichnung nimmt hier vorweg, was erst im Abschnitt über das Intraclass-Modell behandelt wird; der
Ausdruck kann als Intraclass-Kovarianz interpretiert werden. Mit Hilfe dieser Kurzbezeichnungen lautet die
obige Beziehung etwas übersichtlicher (Gesamtvarianz auch in Sigma-Notation):
 2x   xx   IC( x , I )
Betrachtung der Mittelwerte
Bei der Betrachtung der Mittelwerte über I Werte kann der Stichprobenprozess in der gleichen Weise betrachtet
werden. Wenn aber mal die j. Gruppe ausgewählt wurde, werden jeweils I Variablen unabhängig voneinander
aus der Verteilung der Zufallsvariable xj gezogen und deren Mittelwert gebildet.
Erwartungswert des Mittelwerts in der j. Gruppe ist E(x j (I)) = E( 1I ix ij )  (g j1 , g j ] (Kurz:  j ).
Varianz des Mittelwerts über unabhängige Zufallsvariablen in der j. Gruppe ist Var (x j (I)) = Var ( 1I ix ij )
2
= (I unabhängige Züge aus der gleichen Verteilung) = 1I Var ( x j ) = 1I  x (g j1 , g j ]
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 26
Varianz der Mittelwerts-Zufallsvariablen, gemittelt über jeweils alle I Zufallsvariablen jeweils einer Gruppe:
Var ( x (I)) = 1I Var ( x )  IIJ1  j1 ((g j1 , g j ]  ) 2 , wobei Ex ( ) der Erwartungswert der Zufallsvariablen x ist
J
und (g j1 , g j ] der Mittelwert der Verteilung im j. Quantilsbereich ist.
 j1 1J ( j  ) 2  1J  j1 1I Var (x j ) = (Auf Grund der obigen Formel für die Gesamtvarianz gilt
J
J
1
Var ( x j )  Var ( x )  1J  j1 ( j  ) 2 , nach Einsetzen folgt) =
J  j1
J
J
J
 j1 1J ( j  ) 2  1I Var (x)  1J 1I  j1 ( j  ) 2 = 1I Var (x)  IIJ1  j1 ( j  ) 2 . Qed.
Denn: Var ( x (I)) =
J
J
Die Varianz der Mittelwerts besteht daher aus der Summe zweier Teile, wobei sich der erste (= 1I Var (x) ) so
verhält, wie bei völlig zufälligem Ziehen aus der x-Verteilung und bei größer werdenden Gruppen stark kleiner
wird, während der zweite Teil die Between-Gruppen-Varianz (= IIJ1  j1 ( j  ) 2 ) darstellt, die auch bei
J
größer werdenden Gruppen relativ konstant bleibt.
In der oben eingeführten Kurznotation lautet die Formel für die Varianz des Mittelwerts:
Var ( x (I)) = 1I  xx   IC( x ,I) .
Vergleich der Varianzen und Kovarianzen bei Gruppierung nach x
Für die Gruppierung nach x können auch die Kovarianzen und restlichen Varianzen entsprechend berechnet
werden. Die Anwendung für die Gruppierung nach y könnte nach den gleichen Prinzipien erfolgen, die schon
bei der Behandlung der Ordnungsstatistiken dargelegt wurden (über die Hilfsregressionen).
Beispiel: Zum Vergleich mit dem exakten Approach über die
Beispiel: Die Gesamtheit sei n = 1000. Die Graphik zeigt
Ordnungsstatistiken werden hier nochmals die Varianzen und Kovarianzen
wiederum die Varianzen und Kovarianz .
für die
Gruppierung nach x (auf Ordnungstatistkbasis)
Gruppierung nach x (Zweistufiger Approach)
Gruppierung
nach x gezeigt.
Var(x)
Cov(x,y)
Var(y)
Var(e)
Die
Übereinstimm
ung ist so gut,
dass auf der
Grundlage der
Graphiken
keine
Unterschiede
erkennbar
sind.
Gruppenanzahl
Var(x)
Cov(x,y)
Var(y)
Var(e)
Gruppenanzahl
Die Varianzen und Kovarianzen, die mit Hilfe der Annäherung berechnet werden, stimmen sehr gut mit jenen
überein, die auf der Basis der Ordnungsstatistiken berechnet wurden. Die Unterschiede bewegen sich im Bereich
der 4. Dezimalstelle (ca. in der Größenordnung von weniger als einem Promille der Größen).
Berechnung der Intraclass-Kovarianzen
Diese Gruppierungsart hat Konsequenzen für die Intraclass-Kovarianz. Die x-Variablen zweier unterschiedlicher
UEen sind nicht mehr stochastisch unabhängig; es wird nun unterstellt, dass diese Abhängigkeit durch die Intraclass-Kovarianz aufgefangen werden kann. Formal muss dann die gemeinsame Verteilung je zwei solcher xVariablen untersucht werden..
Die Berechnung der Intraclass-Kovarianz berücksichtigt hier, dass die x-Variable als stetige Variable konzipiert
ist; es handelt sich daher um die stetige Variante der Berechnung von Intraclass-Kovarianzen. Obwohl im
Rahmen der Simulation nur der Normalverteilungsfall interessiert, wird zuerst die allgemeine Konzeption
vorgestellt.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 27
Beispiel: Angenommen, die x-Variable sei gleichverteilt
(zwischen 0 und 1). Ihre Dichtefunktion ist f(x) = 1 . Dann ist
die Wahrscheinlichkeit, dass bei zufälligen Ziehen ein Wert
zwischen a und b angenommen wird, wegen der
Gleichverteilungsannahme besonders leicht zu berechnen:
Die beiden stetigen Zufallsvariablen Xc und Xd (x-Variable
für eine c. und d. UE) sind ohne Restriktion auf
Gruppengrenzen unabhängig; ihre Verteilung kann durch die
Dichtefunktion f(xc,xd) = f(xc)*f(xd) beschrieben werden.
Gegeben seien J+1 Gruppengrenzen (gj, j=0,..., J) der J
Gruppen; die entsprechenden Bereiche (bj, j=1,..., J) mit bj =
(gj-1, gj]. Die Wahrscheinlichkeit, dass die beiden Zufallsvariablen Werte innerhalb der j. Gruppe annehmen ist durch
das Integral gegeben: W(X i  b j , X k  b j ) =
gj
gj

gj
 f (x c , x d )dx c dx d =

=
g j1
gj
Die Wahrscheinlichkeit, dass beide Zufallsvariablen im j.
Bereich liegen, unter der Bedingung, dass sie gemeinsam in
einem der Bereiche liegen W Xc  b j , Xd  b j | Xc , Xd gB

= W(Xc  b j , Xd  b j , (Xc , Xd gB)) / W(Xc , Xd  gB) .
Die Dichtefunktion der beiden eingeschränkt variierenden
f ( x c )f ( x d )
Zufallsvariablen ist f gB ( x c , x d ) 
(für
W(Xc , Xd  gB)
Punktpaare ( x c , x d ) aus gB)
f gB ( x c , x d ) 
 
1
W ( X c , X d  gB)
  (x c   c )( x d   d )f gB (x c , x d )dx c dx d
j 
g j1
 (x d   d )f (x d )dx d ,
mit c 
1
W ( X c , X d  gB)
f gB ( x c , x d ) 
j 
g j1
1 (definiert für den eingeschränkten
0.52
1 .
0.52
0.6
0.6
0
1
0
1
0.6
0.6
Cov(Xi , Xk ) =
gj
x cf (x c )dxc
= (b-a)2.
Die Intraclass-Kovarianz im Definitionsbereich (das sind
hier die beiden Bereiche zwischen 0 und 0.60 und zwischen
0.60 und 1) ist für die gegebene Verteilung
g j1
gj
a
c =d = (0.18*0.6+0.32*0.4)/0.52 = 0.454 (  =0.5; denn
die Gruppen sind ungleich groß. i ist näher bei der größeren
Gruppe.
=
gj
(x c   c )f (x c )dx c
a
Bereich).
Die Intraclass-Kovarianz ist die für die eingeschränkte
Verteilung berechnete Kovarianz der beiden Zufallsvariablen
Xc und Xd:
 
gj
b
Unter der Bedingung, dass nur diese Konstellationen
zulässig sind, d.h. dass die Zufallsvariablen jeweils nur werte
im ersten oder 2. Bereich annehmen könne, erhält man die
Verteilung der Wertepaare in den 2 Bereichen durch Division
der obigen Summanden durch die Summe (das entspricht der
Berechnung der
Bereich
Wahrscheinlichkeit
bedingten
Wahrscheinlichkeiten):
1.
0.36/ 0.52
2.
0.16/ 0.52
Die Dichtefunktion der
beiden eingeschränkten Zufallsvariablen ist daher:
g j1

b
  f (x c , x d )dx c dx d =  1dx c  1dx d
Angenommen, es seien 3 Grenzen für 2
Bereiche
Bereiche gegeben: 0, 0.60, 1. Dann ist die
Wahrscheinlichkeit, dass beide gezogenen
Werte jeweils im gleichen Bereich liegen,
gleich der Wahrscheinlichkeit, dass beide Züge
im 1. oder 2. Bereich liegen: 0.602+ 0.402 = 0.52.
 f (x d )dx d .

gj
g j1 g j1
gj
f ( x c )dx c
g j1
Cov(Xc , Xd ) =
a
gj
 f (x d )dx d .
f ( x c )dx c
WX c  b1 , X d  b1   X c  b 2 , X d  b 2     X c  b J , X d  b J 
j 
a
Zufallsvariablen zweier zufälliger Züge eine gemeinsame
bivariate Gleichverteilung. D.h. die Wahrscheinlichkeit, dass
beide Werte in dem Bereich liegen W(Xc  (a, b], Xd  (a, b])
Die Wahrscheinlichkeit, dass die beiden Zufallsvariablen im
gleichen Bereich zu finden sind (im ersten, zweiten oder
einem andern liegen) ist gleich der Summe dieser
Wahrscheinlichkeiten: W(Xc , Xd  gB) =
=
b
 f (x c )dx c =  1dx c = (b-a). Dann haben die beiden
gj
g j1
g j1 g j1
b
 f (x d )dxd und
1
0.52
g j1
1
0.52
 (x c  c )dxc  (x d  d )dxd +
 (x c  c )dxc  (x d  d )dxd =
0.09232 0.13852
0.52
= 0.0533.
 c   d . Falls die Gruppen gleich groß sind, gilt zudem
 c   d   (=Populationsmittelwert der Werte selbst).
(Hinweis zur Integration:
 ( x  )dx =
1
2
x 2  x )
Bei der vorliegenden Gruppierung nach x wurden die Gruppen gleich groß gewählt. Wenn J die Anzahl der
gewünschten Gruppen sind, sollen daher alle Gruppen den Anteil 1/J haben. Als Grenzen gj werden die Quantile
zum Quantum j/J verwendet; dann gilt
 j1 J1
J
2
=
1
J
gj
g j1 f (x c )dx c
=1/J. Daher ist W(Xc , Xd  gB) =


 j  g j1 f (x c )dx c 
gj
2
=
. Da zudem die Gruppen gleich groß sind gilt  c   d   . Daher ist die Kovarianz Cov(Xc , Xd )
2
 gj

= J  j   ( x  )f ( x )dx  =
g
j

1


1
J


 j  J g j1 (x  )f (x )dx 
gj
2
.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 28
Beispiel: Sei J=2, x sei standardnormalverteilt (=0, =1).
Die x-Werte werden aus einer normalverteilten Population
mit der Dichtefunktion f(x)=
1
 2
 x  
 12 

e   
0
2
Dann ist etwa
gezogen; die

Dichtefunktion für einen Gruppenauschnitt wurde oben beim
zweistufigen Modell mit nd(x) abgekürzt.
Das Integral ist
 ( x  ) nd(x )dx =

 x  
1

J e 2   
2
2
; das
bestimmte Integeral für die Quantile a und b lautet
b
 (x  )nd(x)dx =
a
 a  
1

J (e 2   
2
2
 b  
1

2  
e
2
) =
 2 (nd(a )  nd(b)) =: (a, b]   . Das ist zugleich die
Differenz des Gruppenmittels zum Gesamtmittel.
Die Intraclass-Kovarianz kann daher folgendermaßen
dargestellt werden: Cov(Xc , Xd ) =
1
J
 j (g j1 , g j ]  
2
Das ist der Mittelwert der Quadrate der Abweichungen der
Gruppenmittelwerte vom Gesamtmittelwert. Diese Größe
entspricht der mittleren Between-Quadratsumme.
2  xf ( x )dx =
.
2
2
e


 e 0 =
2 =
2
-0.8.
Das ist der
Mittelwert
0.3
über die linke
0.2
Seite der
Standardnorm
0.1
alverteilung.
-2 -1
0
1
2
Da der
Gesamtmittel
(,0]
wert in der
Standardnorm
alverteilung 0 ist, ist –0.8 zugleich die Differenz zum
Gesamtmittelwert.
Bei J=2 sind die 3 Quantile g0 = -, g1 = 0, g2 = .
Die Intraclass-Kovarianz ist dann Cov(Xc , Xd )
= 2J
 1 g2
  1 g2
 j  e 2 j1  e 2 j


= 22 

 
2

 = (mit J=2)


2
2
e   e 0  e 0  e   = 2 = 0.6366


Im Vergleich zur diskreten Variante der Intraclass-Kovarianz ist hier die Intraclass-Kovarianz nur der Mittelwert
der Abweichungsquadrate vom Gesamtmittelwert (das entspricht der Between-Komponente im diskreten Fall);
die Within-Komponente entfällt hier, da wegen der Stetigkeitsannahme die Wahrscheinlichkeit, zwei gleiche
Werte zu ziehen, null ist.
Damit auch an die Abhängigkeit der Intraclass-Kovarianz der x-Werte von der Gruppengröße (= I) erinnert wird,
sei hier als Abkürzung das Symbol verwendet: IC(x,I) = Cov(xc, xd) bei einer Gruppengröße von I.
Beispiel: Intraclass-Kovarianzen mit b=0.5.
Die Intraclass-Kovarianz der x-Werte hat auch
Konsequenzen für die Intraclass-Kovarianz der y-Werte und Mit I = 1000 / Gruppenanzahl.
jene der Intraclass-Kovarianz der Kovarianz zwischen x- und
y-Werte;
Die Intraclass-Kovarianz der y- mit den x-Werten kann auf
Grund der linearen Modells aus Cov(xc, xd) berechnet
werden: IC(y,x,I) = Cov(yc, xd) = Cov(a+bxc+ei, xd) = b
Cov(xc,xd)
= b IC(x,I).
Cov(xc , xd )
Cov(xc , yd )
Cov(yc , yd )
Die Intraclass-Kovarianz der y-Werte kann ebenfalls so
berechnet werden:
IC(y,I) =Cov(yc, yd) =Cov(a+bxc+ec, a+bxd+ed)
= b2 Cov(xc, xd) = b2 IC(x,I).
Je kleiner die Gruppen sind, desto größer ist die IntraclassKovarianz. Die Intraclass-Kovarianz erreicht maximal die
Varianz bzw. Kovarianz der Variablen selbst.
Ab einer Gruppenanzahl von ca. 10 (das entspricht hier einer
Gruppengröße von 100 und kleiner) bleiben die IntraclassKovarianzen in etwa auf der gleichen Höhe.
Varianzen und Kovarianzen der Mittelwerte der Variablen bei Gruppierung nach x
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 29
Beispiel: Die Gesamtheit auf der 1. Stufe sei n = 1000. Die
Graphik zeigt wiederum die Varianzen und Kovarianz .
Gruppierung nach x (Intraclass-Annäherung)
Bei der Gruppierung nach x wirken sich die IntraclassKovarianzen stark auf die Varianzen und Kovarianzen der
Mittelwerte aus. Sie werden hier jeweils so als Summe
zweier Teile geschrieben, deren 1. Teil die starke
Abhängigkeit von der Gruppengröße zeigt und deren 2. Teil
den relativ konstanten Teil der Intraclass-Kovarianzen
enthält.
 y ( I) 
Var  x (I) =
 e(I) 
1
I
Var(x)
e2  b 2 (2x  IC( x , I ) ) b(2x  IC( x , I ) ) e2
b(2x  IC( x , I ) )
2x  IC( x , I )
0
2
e
0
e2
Cov(x,y)
Var(y)
Var(e)
b 2 IC( x , I ) b IC( x , I ) 0
+ b IC( x , I )  IC( x , I ) 0 .
0
0
0
Gruppenanzahl
Während die Varianz von x und die Kovarianz ab der
Alle Varianzen bzw. Kovarianzen der Mittelwerte in x bzw. y Gruppenanzahl von 10 fast gar nicht mehr ansteigt, steigt die
Varianz mit der Gruppenanzahl fast so stark wie bei der
enthalten 2x  IC( x, I) und  IC( x , I ) .  IC( x , I ) ist für I <100
Zufallsgruppierung (das liegt in erster Linie daran, dass die
Varianz der y-Mittelwert im 1. Teil den relativ großen
(keine Gruppengrößen, große Gruppenanzahl) fast gleich
Summanden  e2 /I enthält, der stark mit der Gruppenanzahl
2
2
groß wie  x selbst. Daher ist bis dahin x  IC( x, I) fast 0,
variiert). Im unteren Bereich (Gruppenanzahl kleiner 10)
dominieren die Intraclass-Kovarianzen den Verlauf.
erst für I > 100 (große Gruppengrößen, kleine
Gruppenanzahl) wirkt sich auch diese Differenz stärker aus.
Beweise: a) Var ( y(I))  Var ( 1
I
=
I
= 1I

2
y

 (I  1)b 2  IC( x , I) =


1
I
b
2
 2x   e2  (I  1)b 2  IC( x ,I)

b 2  IC( x ,I)  1I  e2  b 2 ( 2x   IC( x , I) ) = b 2  IC( x ,I)  1I ( 2x   IC( x ,I) )  1I  e2 =
b) Var ( x (I)) = 1I
c)


i1 y i )
2
x


 e2  b 2 Var ( x (I)) .
 (I  1) IC( x , I) =  IC( x , I)  1I  2x   IC( x , I) .
Cov ( y(I), x (I))  Cov ( 1I 


1
I

I
y ,1
i 1 i I



I
x )
j1 j

=
1
I
 yx  (I  1) IC( yx,I)  = 1I b 2x  (I  1)b IC( x,I) 

= b IC( x , I)  bI  2x   IC( x , I ) = b  IC( x , I)  1I  2x   IC( x , I) =b Var ( x(I)) . Qed.
Äquivalenz der Mittelwert-Darstellungen
Anhand der Varianz des x-Mittelwertes kann die Äquivalenz gut gezeigt werden. Das wäre auch für die
Varianzen und Kovarianzen der anderen Mittelwerte möglich. Die x-Mittelwert-Varianz ist aber bei der
Gruppierung nach x die grundlegende Komponente auch für die Berechnung der andern Varianzen und
Kovarianzen.
Die Varianz der x-Mittelwerte mit Intraclass-Darstellung Var ( x(I)) =
mit Populationsmittelwertsformulierung Var ( x(I)) =
Denn:
1
I

1
I
 2x  IIJ1  j ((g j1 , g j ]  ) 2 . Qed.
2
x

 (I  1) 1J  j ((g j1 , g j ]  ) 2 =
1
J

2
x
 (I  1) IC( x , I)
 2x  IIJ1  j (g j1 , g j ]  
 IC( x ,I) = 1J  j ((g j1 , g j ]  ) 2 . Daher ist Var ( x(I))
1
I

1
I
= 1I

2
x
2 .
 (I  1) IC( x , I)


ist gleich jener
=
j ((g j1 , g j ]  ) 2  1I   2x  1J j ((g j1 , g j ]  ) 2  =
Schätzung der Varianzen bzw. Kovarianzen
Für die Kreuzprodukte, mit deren Hilfe die Varianzen und Kovarianzen geschätzt werden sollen, werden nun die
Erwartungswerte berechnet. Die Schätzer ergeben sich dann aus den Erwartungswerten nach der Momentenmethode.
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 30
Die Erwartungswerte der Kreuzprodukte (Festgrenzenannäherung)
Vorerst sollen die Kreuzprodukterwartungswerte von CPxx.T, CPxx.B und CPxx.W berechnet werden unter der
Voraussetzung, dass die x-Werte nach dem beschriebenen zweistufigen Verfahren aus den nichtüberlappenden
Verteilungen gezogen werden. Die festen Bereiche der Verteilungen werden durch die Quantile begrenzt. Die
Gruppen werden jeweils gleich groß gewählt, anders ausgedrückt: für die Auswahl einer Einheit gilt
Gleichwahrscheinlichkeit hinsichtlich der Gruppen.
Definitionen bzw. Abkürzungen
Die Varianz der Erwartungswerte der Zufallsvariablen x bezüglich der Gruppen-Zufallsvariablen G mit den J
Ausprägungen wird oft bezeichnet als Var G (E( x | G)) = (für die Anwendung mit den Quantilen gj für j=1, ... ,
J und gleiche Wahrscheinlichkeit der J Gruppen ) =
1
J
 j ((g j1 , g j ]  ) 2 = (oder kurz) = 1J  j1 (  j    ) 2 =
J
(bei der Intraclass-Darstellung wurde gezeigt, dass dieser Ausdruck gleich der Intraclass-Kovarianz ist) =
 IC( x ,I) .
Der Erwartungswerte der Varianz der Zufallsvariablen x bezüglich der Gruppen-Zufallsvariablen G mit den J
Ausprägungen wird oft bezeichnet als E G (Var (x | G)) = (für die Anwendung mit gleicher Wahrscheinlichkeit
der J Gruppen ) = 1J  j1 Var ( x j ) = (als Kurzbezeichnung noch ein Symbol) =  xx .
J
Erwartungswerte der Kreuzprodukte für x: Total-, Within- und Between-Kreuzprodukte
Satz: Zusammenfassung; es gilt:
E (CPxx ,T ) = (IJ  1) 1J  j1 Var ( x j )  I j1 (  j    ) 2 = (IJ  1)E G (Var (x | G))  IJVar G (E(x | G)) .
J
J
mit E G (Var ( x | G)) 
1
J
 j1 Var (x j ) und
J
Var G (E( x | G))  1J  j1 (  j    ) 2
J
E(CPxx , W ) = (I  1) j1 Var ( x j ) = J(I  1)E G (Var (x | G)) .
J
E (CPxx , B ) = (J  1) 1J  j1 Var ( x j )  I j1 (  j    ) 2 = (J  1)E G (Var (x | G))  IJVar G (E( x | G)) .
J
Denn:
J
E(CPxx , B )  E(CPxx ,T  CPxx , W ) = E(CPxx ,T )  E(CPxx , W )
(IJ  1)E G (Var (x | G))  IJVar G (E(x | G))  J(I  1)E G (Var (x | G))
= (J  1)E G (Var ( x | G))  IJVar G (E( x | G)) . Qed.
=
Die Behauptungen zu den Erwartungswerten der Total- und der Within-Kreuzprodukte werden in den beiden folgenden Sätzen
bewiesen.
Satz: Der Erwartungswert des Total-Kreuzprodukts ist
E (CPxx ,T ) = (IJ  1) 1J  j1 Var ( x j )  I j1 (  j    ) 2 = (IJ  1)E G (Var (x | G))  IJVar G (E(x | G))
J
Denn:
J
E (CPxx ,T ) =  j1  1 E( x j  x  ) 2 =
J
 j1 1 E(( x j    j )  (x     j )) 2 .
I
J
I
Für jeden Summanden gilt:
E(( x j    j )  ( x     j )) 2 = E( x j    j ) 2  2E( x j    j )( x     j )  E( x     j ) 2
= E( x j    j ) 2  2 IJ1 E( x j    j )( g k ( x kg    j )) 
J
I
= E( x j    j ) 2  IJ2 g k E( x j    j )( x kg    j ) 
J
I
1
I2J 2
1
I2J 2
E(g k ( x kg    j )) 2
J
I
E(g k ( x kg    j )) 2 .
J
I
Die drei Komponenten werden zuerst getrennt betrachtet
g k E(x j    j )( x kg    j ) = IJ2 g k E(x j    j )(( x kg   g )  ( g    j ))
J
I
J
I
2
E( x j    j )( x kg   g )  IJ2 g k E( x j    j )( g    j ) =
IJ g k
2
a) IJ
=
J
I
J
I
Nagl, Multilevel-Modelle, Materialien, Anhang A1
=
j  g,   k
) =
sonst
Var ( x j ),
E( x j    j )( x kg   g )  
0

(wegen
b)
Seite 31
2
IJ
Var (x j )
E(g i ( x ig    j )) 2 = E(g i (( x ig   g )  ( g    j ))) 2
J
I
J
I
g,i f ,t E((( x ig   g )  ( g    j ))(( x tf   f )  ( f
J,I
J,I
Produkte einzeln betrachten:
   j ))) = (Produkte ausmultiplizieren und zuerst
E(((x ig   g )  ( g    j ))((x tf   f )  ( f    j ))) =
E(x ig   g )(x tf   f )  E( g    j )(x tf   f )  E( f    j )(x ig   g )  ( g    j )( f    j ) .
Var ( x g ), g  f , i  t
, bzw.
0
sonst

(Die Erwartungswerte der Produkte sind E ( x ig  g )( x tf  f )  
E( g    j )(x tf   f ) = 0. und E( f    j )(x ig   g ) = 0 )
)
g i t E(x ig   g )( x tg   g )  g,i f g,t E(x ig   g )( x tf   f )
J
+ gJ,,Ii fJ,,It ( g    j )( f    j ) = Ig Var ( x g ) I 2 J 2 (     j ) 2
J
=
I
I
J,I
J,I
c) E( x j    j ) 2 = Var ( x j )
Daher gilt wegen a) , b) und c)
E ( x j  x  ) 2 = E( x j    j ) 2  IJ2 g k E( x j    j )( x kg    j ) 
J
= Var ( x j )  IJ2 Var ( x j ) 
= (1  IJ2 )Var ( x j ) 
1
J 2I

I
1
I2J 2
E(g k ( x kg    j )) 2
J
I

J
1
Var ( x g ) (     j ) 2
g
J 2I
J
Var ( x g ) (     j ) 2
g
 j1  1 (1  IJ2 )Var (x j )  J12I g Var (x g ) (     j ) 2 
Daher gilt für den Erwartungswert des Kreuzprodukts
J
E (CPxx ,T ) =
I
J
g Var (x g ) I j1 (  j    ) 2
J
J
2
= (IJ  1) 1J  Var ( x j )  I (  j    ) . Qed.
j1
j1
=
(I  2IJI ) j1 Var ( x j )  JII
J
J
J
Satz: Der Erwartungswert des Within-Kreuzprodukts ist
E(CPxx , W ) = (I  1) j1 Var ( x j ) = J(I  1)E G (Var (x | G))
J
.
Denn:
E(CPxx , W ) =  j1  1 E( x j  x  j ) 2 .
J
Dabei ist
I
E( x j  x  j ) 2 = E(( x j   j )  ( x  j   j )) 2 =
E( x j   j ) 2  2I k E( x j   j )( x kj   j ) 
I
a) 2
I
k E(x j    j )(x kj    j ) =
I
1
I2
E(i ( x ij   j )) 2 .
I
(Zweistufig betrachtete Erwartungswerte ergeben
Var ( x j )   k
E( x j   j )( x kj   j )  
k
 0
2
) = I Var ( x j ) .
b)
E(i (x ij    j )) 2 =
I
i k E((x ij    j )(x kj    j )) = (Zweistufig betrachtete Erwartungswerte ergeben
I
I
Var ( x j ) i  k
E( x ij    j )( x kj    j )  
ik
 0
) = IVar(x j )
c) E( x j    j ) 2 = Var ( x j )
Nagl, Multilevel-Modelle, Materialien, Anhang A1
Seite 32
Daher gilt wegen a) , b) und c)
E( x j  x  j ) 2 = Var ( x j )  2I Var ( x j )  1I Var ( x j ) =
Daher gilt:
=
Var ( x j ) .
E(CPxx , W )
 1 II1 Var (x j ) = (I  1) j1 Var (x j ) =
J
j1
I1
I
I
J
J(I  1)E G (Var (x | G))
Formeln der Populationsvarianzen der Variablen x und des Mittelwerts
Die Populationsvarianzen sollen geschätzt werden, gesucht sind die Schätzer für folgende Varianzen:
Für die Zufallsvariable Var ( x ) = 1J  j1 Var ( x j )  1J  j1 ( x (g j1 , g j ]  ) 2 = E G (Var (x | G))  Var G (E(x | G))
J
J
= (in Kurzbezeichnung) =  xx   IC( x,I)
Für den Mittelwert über I Werte Var ( x (I)) = 1I Var ( x)  IIJ1  j1 ((g j1 , g j ]  ) 2 =
J
1
I
1
I
E G (Var (x | G))  VarG (E(x | G))  II1 VarG (E(x | G)) =
E G (Var (x | G))  VarG (E(x | G)) = (in Kurzbezeichnung) =
1
I
 xx   IC( x ,I)
Erwartungstreue Schätzer für die Varianzen
Auf Grund der Berechnung der Erwartungswerte ergeben sich die Gleichungen:
E(CP xx ,T )  (IJ  1)  xx  IJ IC( x , I)
E(CP xx , B )  (J  1)  xx  IJ IC( x , I)
Es sei daran erinnert, dass die entsprechenden Kreuzprodukte auch TSS (für das Total-Kreuzprodukt in x etwa)
und BSS (für das Between-Kreuzprodukt) bezeichnet wurde.
Entsprechend der Gleichsetzung von Erwartungswerten mit den Werten nach den Prinzipen der
Momentenmethode:
TSS  (IJ  1) ˆ xx  IJˆ IC( x ,I)
BSS  (J  1) ˆ  IJˆ
xx
IC( x , I )
Das Auflösen dieses Gleichungssystems liefert die Schätzer:
ˆ IC( x ,I)

ˆ xx

( IJ 1) BSS ( J 1) TSS
J 2 ( I 1) I
TSS  BSS
J ( I 1)
bzw. etwas anders formuliert:
ˆ xx

ˆ IC( x , I )

1
(CP xx ,T  CP xx , B )
J ( I 1)
.
1
(CP xx ,T  (IJ  1) ˆ xx )
JI
Da Linearkombinationen erwartungstreuer Schätzer wiederum erwartungstreu sind, können die beiden
interessierenden Varianzen erwartungstreu geschätzt werden:
Schätzer der Varianz der Mittelwerte über I x-Variablen jeweils einer Gruppe: V̂ar(x(I)) = 1I ˆ xx  ˆ IC( x , I)
bzw. der Varianz für x selbst: V̂ar( x ) = ˆ xx  ˆ IC( x , I) .