GK Mathematik, 13d Übungen: Exponentialfunktionen

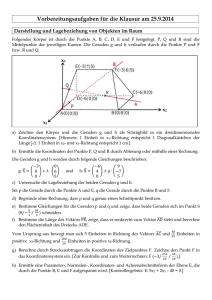
Vorbereitungsaufgaben für die Klausur am 25.9.2014
1 Hilfsmittelfreier Teil
a) Berechne mit dem GAUSS-Verfahren die Lösungsmenge des folgenden linearen Gleichungssystems:
3
1
−1
2
−1
0,5
−1
1
2 | −1
−1
3
b) Bestimme eine Funktionsgleichung f(x) einer ganzrationale Funktion f dritten Grades, deren Graph
punktsymmetrisch zum Ursprung ist und im Punkt H (1/2) einen lokalen Hochpunkt besitzt.
c)
Ermittle die Lösungsmenge für das 1x3-LGS x1 + x2 + x3 = 1.
d) Ermittle die Lösungsmenge für das 2x3-LGS: x1 + x2 + x3 = 1 und x1 + 2x2 + 3x3 = 4.
e) Interpretiere die Ergebnisse aus c) und d) geometrisch.
f)
2
1
3
5
Gegeben sind die beiden Geraden g: ⃗X = (2) + λ ⋅ (2) und h: ⃗X = (3) + μ ⋅ (5). Projiziert man g und h senkrecht
1
3
2
3
in die x1-x2−Koordinatenebene, so erhält man die Geraden g´ und h´.
f1) Gib die Gleichungen der Geraden g´ und h´ in Parameterform an.
f2) Untersuche die Lagebeziehung von g´ und h´.
2 Darstellung und Lagebeziehung von Objekten im Raum
Folgender Körper ist durch die Punkte A, B, C, D, E und F festgelegt. P, Q und R sind die Mittelpunkte der jeweiligen
Kanten. Die Geraden g und h verlaufen durch die Punkte P und F bzw. R und Q.
x3
x2
x1
a) Zeichne den Körper und die Geraden g und h als Schrägbild in ein dreidimensionales Koordinatensystem.
[Hinweis: 1 Einheit in x1-Richtung entspricht 1 Diagonalkästchen der Länge 12√2. 1 Einheit in x2- und x3-Richtung
entspricht 1 cm.]
b) Ermittle die Koordinaten der Punkte P, Q und R durch Ablesung oder mithilfe einer Rechnung.
Die Geraden g und h werden durch folgende Gleichungen beschrieben:
−3
0
g: ⃗X = ( 0 ) + λ ⋅ (6)
0
5
c)
und
−6
9
h: ⃗X = ( 4 ) + μ ⋅ (−7)
0
5
Untersuche die Lagebeziehung der beiden Geraden g und h.
Sei p die Gerade durch die Punkte A und E, q die Gerade durch die Punkte B und F.
d) Begründe ohne Rechnung, dass p und q genau einen Schnittpunkt besitzen.
8
e) Bestimme Gleichungen für die Geraden p und q und zeige, dass beide Geraden sich im Punkt S (8/− /
3
schneiden.
40
3
)
f)
Bestimme die Länge des Vektors ⃗⃗⃗⃗
PE, zeige, dass er senkrecht zum Vektor ⃗⃗⃗⃗⃗
AD steht und berechne den Flächeninhalt
des Dreiecks ADE.
⃗⃗⃗⃗⃗ und
Vom Ursprung aus bewegt man sich 5 Einheiten in Richtung des Vektors AC
und
100
29
40
29
Einheiten in positive x3-Richtung
Einheiten in positive x2-Richtung.
g) Berechne durch Streckenabtragen die Koordinaten des Zielpunktes F. Zeichne den Punkt F in das
216
40
Koordinatensystem ein. [Zur Kontrolle und zum Weiterrechnen: F (−3/
/ ).]
29
29
h) Ermittle eine Parametergleichung der Ebene E, die durch die Punkte B, C und F aufgespannt wird.
0
1
3
[Kontrollergebnis zum Weiterrechnen: E: ⃗X = (8) + r ⋅ (0) + s ⋅ ( 2 )]
0
0
−5
i)
Zeige durch Punktprobe, dass der Punkt F in E liegt.
j)
Der Punkt T ist Mittelpunkt der Strecke AC. Ermittle die Koordinaten von T und zeichne ihn in das
Koordinatensystem ein. [Kontrollergebnis: T(−3/4/0).]
⃗⃗⃗⃗ sowie seine Länge d = |TF
⃗⃗⃗⃗ | und zeige, dass TF
⃗⃗⃗⃗ senkrecht zur Ebene E steht. Gib die
k) Berechne den Vektor TF
⃗⃗⃗⃗ senkrecht zu beiden Richtungsvektoren der Ebene E ist.]
Bedeutung von d an. [Hinweis: Zeige, dass TF
l)
Berechne den Schnittpunkt der Ebene E mit der Gerade g AE durch die Punkte A und E.
m) Für Experten: Die Ebene F wird durch die Punkte A, D und E aufgespannt und hat die Gleichung. Ermittle eine
Gleichung für die Schnittgerade der beiden Ebenen E und F. [Tipp: Durch gleichsetzen erhältst Du ein LGS mit
drei Gleichung und vier Unbekannten, das unendlich viele Lösungen besitzt und daher als Lösungsvektor einen
Geradenvektor besitzt.]
3 Bewegungsaufgaben
Ein Flugzeugt F1 befindet sich zum Beobachtungsbeginn t = 0 im Punkt A (-16/-8/8). Vier
Minuten später wird der Standort B (16/16/8) ermittelt. Dabei entspricht eine Einheit
einem Kilometer. Ein Flughafen befindet sich im Punkt C (0/0/0). Die Startbahn des
Flughafens liegt in der x1x2-Ebene.
a) Begründe im Sachzusammenhang, dass das Flugzeug F1 durch folgende Gleichung
beschrieben wird:
−16
8
F1 : ⃗X = ( −8 ) + t ⋅ (6)
8
0
(t in Minuten).
b) Ermittle den Standort des Flugzeuges zwei Minuten vor und acht Minuten nach Beobachtungsbeginn. (4P)
c)
Berechne die Geschwindigkeit des Flugzeuges F1 in km/h.
d) Untersuche die Gerade F1 auf ihre besondere Lage im Koordinatensystem und interpretiere das Ergebnis im
Sachzusammenhang. [Hinweis: Betrachte den Geschwindigkeitsvektor von F1.]
Ein zweites Flugzeug F2 startet beim Beginn der Beobachtung vom Flughafen C. Seine Flugbahn kann für die ersten
fünf Minuten durch folgende Gleichung beschrieben werden:
2,5
F2 : ⃗X = r ⋅ (3,125) (r in Minuten).
2,5
Eine Wolkendecke befindet sich 2 km über der Landebahn.
e) Bestimme den Zeitpunkt, an dem das Flugzeug F2 die Wolkendecke durchbricht und berechne den
Durchbruchpunkt D.
f)
Beurteile das Risiko einer Kollision zwischen den Flugzeugen F1 und F2.
Die Spitze eines Gebirges befindet sich in E (-16/92/1).
g) Ermittle einen Lösungsansatz, wie Du den Zeitpunkt bestimmen kannst, an dem das Flugzeug F 1 den geringsten
Abstand vom Punkt E hat. [Hinweis: Hier muss nicht gerechnet werden.]
h) Berechne den Zeitpunkt der geringsten Entfernung des Flugzeuges F1 zum Punkt E und gib einen Wert für diese
Entfernung an.
Lösungen
3
1a) 1
−1
x
2 −1
3 2 −1
1
1
3 2 −1
1
3 2 −1 1
−5
−1 2 | −1 ⇔ 0 5 −7 | 4 ⇔ 0 5 −7 | 4 ⇔ 0 5 −7 | 4 ⇔ (y) = ( 12 )
z
0,5 −1
0 3,5 −4 10
3
0 0 −9 −72
0 0 1
8
8
1b) Man erhält mit f(1) = 2, f´(1) = 0 für f(x) = ax3 +bx (f ist ungerade) und f´(x) = 3ax2 + b das LGS mit Unbekannten a und b:
1 1 2
1 1
2
1 1
2
|

| 
|
 a = −1, b = 2 − a = 3  f(x) = −x 2 + 3x
3 1 0
0 −2 2
0 1 −1
1c) Wählt man x2 = r und x3 = s, so erhält man x1 = 1 r – s. Schreibt man dies als Lösungsvektor, so erhält man die Parametergleichung der Ebene
1
−1
−1
⃗X = (0) + r ⋅ ( 1 ) + s ⋅ ( 0 )
0
0
1
1d) x1 + x2 + x3 = 1 und x1 + 2x2 + 3x3 = 4 lässt sich reduzieren zu x2 + 2x3 = 3 (zweite Gleichung minus erste Gleichung). Wählt man x3 = t, ergibt sich
−2
x2 = 3 – 2t und x1 = 1 – x2 – x3 = 1 – (3 – 2t) – t = -2 + t. Der Lösungsvektor beschreibt die folgende Parametergleichung einer Geraden: ⃗X = ( 3 ) + t ⋅
0
1
(−2).
1
1e) Interpretation: Durch jede Gleichung wird eine Ebene beschrieben. Der Schnitt zweier Ebenen ist im Falle von d) eine Gerade.
1
2
3
5
⃗ = (2) + λ ⋅ (2) und h´: X
⃗ = (3) + μ ⋅ (5) (Bei der senkrechten Projektion in die x1-x2−Koordinatenebene ist die x3-Koordinate des
1f1) g´: X
0
0
0
0
Geradenpunktes immer Null.).
1 f2) Die Geraden g´ und h´ sind echt parallel oder identisch, da die Richtungsvektoren kollinear sind. Der Vektor vom Aufpunkt G´ von g´ zum
Aufpunkt H´ von h´ (Differenzverktor der Stützvektoren) ist offenbar nicht kollinear zu den Richtungsvektoren der Geraden g´ und h´. g´ und h´
sind also echt parallel.
2a) klar 2b) P (-3/0/0), Q (-1,5/0,5/2,5), R (-6/4/0)
2c) Da die beiden Geraden g und h offenbar nicht parallel sind (warum?), setzen wir gleich:
9μ
−6 + 9μ
−3
0
−6
9
−3
3
( 0 ) + λ ⋅ (6) = ( 4 ) + μ ⋅ (−7) ⇔ ( 6λ ) = ( 4 − 7μ ) ⇔ (6λ + 7μ) = (4)
5μ
5λ − 5μ
0
5
0
5
5λ
0
1
1
1
1
3
3
3
3
Durch Gleichung (I) erhält man μ = . Mit Gleichung (III) ergibt sich auch λ = . Setzt man λ und μ in Gleichung (II) ein, ergibt sich 6 ⋅ + 7 ⋅ = 4,
1
also 4 = 4 (f). Daher sind die beiden Geraden windschief.
3
2d) Die Kanten AE und BF sind die offenbar nicht parallelen Kanten eines (ebenen) Trapezes. Daher liegen die nicht parallelen Geraden in einer
Ebene. Sie haben daher genau einen Schnittpunkt.
−3
0
−3
2e) Die Geradengleichungen lauten: p: ⃗X = λ ⋅ ( 1 ), q: ⃗X = (8) + μ ⋅ (−2)
5
0
5
Nun kann durch Punktprobe überprüft werden, dass der Punkt S auf p und q liegt:
−3
0
−3
8
S⃗ = λ ⋅ ( 1 ) und S⃗ = (8) + μ ⋅ (−2) liefert jeweils ein eindeutiges μ = λ = .
3
5
0
5
Alternativ kann mit mehr Aufwand auch das Gleichsetzungsverfahren angewendet werden:
−3μ
3λ − 3μ
−3
0
−3
0
−3λ
λ ⋅ ( 1 ) = (8) + μ ⋅ (−2) ⇔ ( λ ) = (8 − 2μ) ⇔ ( λ + 2μ ) = (8)
5μ
5λ − 5μ
5
0
5
0
5λ
8
8
Gleichung (I) und (III) ergeben jeweils λ = μ. Ersetzt man in (II) μ durch λ, ergibt sich μ = λ = . Setzt man λ = in die Gleichung von g ein, erhält
3
3
man den Schnittpunkt S.
0
⃗⃗⃗⃗ | = √26 ≈ 5,10. Wegen ⃗⃗⃗⃗
2f) Es gilt ⃗⃗⃗⃗
PE = ⃗E − ⃗P = (1) und damit |PE
PE ∙ ⃗⃗⃗⃗⃗
AD = 0 sind beide Vektoren senkrecht zueinander. Insbesondere ist PE die
5
Höhe auf der Seite AD im Dreieck ADE.
Damit erhält man für den Flächeninhalt A des gleichschenkligen Dreiecks mit der Grundseitenlänge 6: A = 12 ⋅ 6 ⋅ √26 = 3 ⋅ √26 ≈ 15,30.
−3
0
−6
0
0
0
−6
0
0 216
1
40
100
1
40
100
⃗
2g) F = (0) + 5 ⋅
∙ ( 8 ) + ∙ (0) +
∙ (1) = (0) + 5 ⋅ ∙ ( 8 ) + ∙ (0) +
∙ (1) ( 29 ≈ 7,4)
29
29
10
29
29
√(−6)2 +82
40
0
0
0
0
0
0
1
1
≈ 1,4
29
0
−6
−3
0
1
3
2h) E: ⃗X = ⃗B + r ⋅ ⃗⃗⃗⃗⃗
BC + s ∙ ⃗⃗⃗⃗
BF = (8) + r ⋅ ( 0 ) + s ∙ (−2) = (8) + λ ⋅ (0) + μ ∙ ( 2 )
0
0
5
0
0
−5
−3 = λ + 3μ ⇒ λ = −1,8964
0
1
3
216
2i)( 29 ) = (8) + λ ⋅ (0) + μ ∙ ( 2 ) ⇔ 29 = 8 + 2μ ⇒ μ = −0,2759
40
40
0
0
−5
= −5μ ⇒ μ = −0,2759
−3
216
29
29
Damit liegt der Punkt F für λ = −1,8964 und μ = −0,2759 in E.
0
−6
−3
⃗ = (0) + 1 ∙ ( 8 ) = ( 4 ).
2j) T ist Mittelpunkt der Strecke AC, also gilt T
2
0
0
0
−3
0
−3
0
0
1
0
216
100
⃗⃗⃗⃗ = F
⃗ −T
⃗ = ( 29 ) − ( 4 ) = ( 29 ) = 20 ∙ (5) ⇒ TF
⃗⃗⃗⃗ ist senkrecht zu beiden Richtungsvektoren der Ebene E, da 20 ∙ (5) ⋅ (0) = 0 und 20 ∙ (5) ⋅
2k) TF
29
29
29
40
40
0
0
2
2
2
29
29
3
100 2
40 2
20√29
( 2 ) = 0 (Vorfaktor kann auch weggelassen werden). d = TF = √( ) + ( ) =
≈ 3,7 ist der Abstand des Punktes T von der Ebene E.
29
29
29
−5
−3
0
1
3
⃗ = t ⋅ ( 1 ) und E: X
⃗ = (8) + r ⋅ (0) + s ⋅ ( 2 ). Durch Gleichsetzen erhält man folgendes LGS für die Unbekannten r, s und t:
2l) g AE : X
5
0
0
−5
1 3
3
0
8
8
8
40
0 2 −1 | −8. Der GTR ermittelt r = 0, s = − 3, t = 3. Damit ergibt sich als Schnittpunkt der Punkt S (-8/ 3 / 3 ).
0 −5 −5
0
0
1
3
1
−3
2m) Durch Gleichsetzen erhält man: (8) + r ⋅ (0) + s ⋅ ( 2 ) = t ⋅ (0) + u ⋅ ( 1 ).
0
0
−5
0
5
In der Matrizenschreibweise für die Unbekannten r, s, t und u bekommt man:
1 3 −1 3
1 3 −1 3
0
0
0 2 0 −1 | −8 ⇔ 0 2 0 −1 | −8 .
0 −5 0 −5
0 0 0 −15 −40
0
8
8
Es ergibt sich u = . Setzt man u in die zweite Gleichung ein, folgt s = 0,5u – 4 = − . Setzt man nun s und u in die erste Gleichung ein, folgt: r – t = 3
3s – 3u = 0, also r = t = μ. Setzt man z. B. u =
8
3
3
in der Parametergleichung der Ebene F ein, ergibt sich eine Geradengleichung als Lösungsvektor:
−8
1
−3
1
8
⃗X = t ⋅ (0) + 8 ⋅ ( 1 ) = ( 3 ) + t ⋅ (0). Dies ist eine zur x1-Achse parallele Gerade (Warum?).
3
40
0
5
0
3
3a) Der Stützvektor der Geraden entspricht dem Ortsvektor zum Startpunkt der Beobachtung bei t = 0. Der Richtungsvektor der Geraden F1
entspricht 14 ⋅ ⃗⃗⃗⃗⃗
AB, da das Flugzeug für die Strecke von A nach B vier Minuten braucht und t in Minuten angegeben ist.
−16
8
−32
−16
8
48
3b) ⃗X(−2) = ( −8 ) + (−2) ⋅ (6) = (−20), ⃗X(8) = ( −8 ) + 8 ⋅ (6) = (40)
8
0
8
8
0
8
3c) In einer Minute legt das Flugzeug die Länge des Geschwindigkeitsvektors zurück. Dieser Vektor hat die Länge √82 + 62 + 02 = 10 km. Daher
beträgt die Geschwindigkeit des Flugzeuges 600 Kilometer pro Stunde.
3d) Die Gerade F1 hat für jedes t den x3-Wert 8 (x3-Komponente des Geschwindigkeitsvektors ist Null), so dass sie parallel zur x 1x2-Ebene verläuft.
Dies bedeutet, dass das Flugzeug mit einer konstanten Flughöhe von 8 km fliegt.
3e) Die Bedingung für das Durchstoßen der Wolkendecke lautet x3 = 2. Also:
x1
2,5
2,5
2
⃗⃗ = (x2 ) = r ⋅ (3,125) ⇒ 2 = 2,5r ⇒ r = 0,8 ⇒ D
⃗⃗ = 0,8 ⋅ (3,125) = (2,5)
D
2
2,5
2,5
2
Nach 48 Sekunden durchstößt das Flugzeug bei D (2/2,5/2) die Wolkendecke.
3f) Durch Gleichsetzen der beiden Geradengleichungen erhält man:
2,5
8t − 2,5r
−16
8
16
( −8 ) + t ⋅ (6) = r ⋅ (3,125) ⇔ (6t − 3,125r) = ( 8 )
2,5
2,5r
8
0
8
Gleichung (III) ergibt r = 3,2. r eingesetzt in Gleichung (II) erzeugt t = 3. Beide Parameter r und r erfüllen Gleichung (I). Daher schneiden sich die
beiden Geraden F1 und F2. Flugzeug F1 erreicht den Schnittpunkt nach 3 Minuten, Flugzeug F2 nach 3 Minuten und 12 Sekunden. Es besteht
prinzipielle keine Gefahr des Zusammenstoßes. Dennoch sollte Flugzeug F2 aufgrund der knappen Zeitspanne bis zum möglichen Kollisionspunkt
seine Geschwindigkeit beim Start entweder ein wenig steigern oder den Start um eine Minute verzögern, um eine Kollisionsgefahr völlig
auszuschließen.
⃗⃗⃗⃗ des allgemeine Geradenpunktes von F1 und dem Punkt E. Dann bestimmt man das Quadrat
3g) Man berechnet zunächst den Verbindungsvektor EX
der Länge dieses Vektors. Dieses Quadrat hängt vom Parameter t ab und wird mit D(t) bezeichnet. Anschließend untersucht man die Funktion D auf
eine globale Minimumstelle, indem man D´(t) = 0 und D´´(t) > 0 überprüft.
8t
⃗⃗⃗⃗ = (6t − 100) ⇒ D(t) = 64t 2 + (6t − 100)2 + 7 = 100t 2 − 1200t + 10049
3h) EX
7
D´(t) = 200t − 1200 ⇔ t = 6. Wegen D´´(t) = 200 > 0, hat das Flugzeug nach 6 Minuten die geringste Entfernung vom Punkt E. Die geringste
Entfernung d beträgt √D(6) ≈ 80,31 km.