superhirn-schach

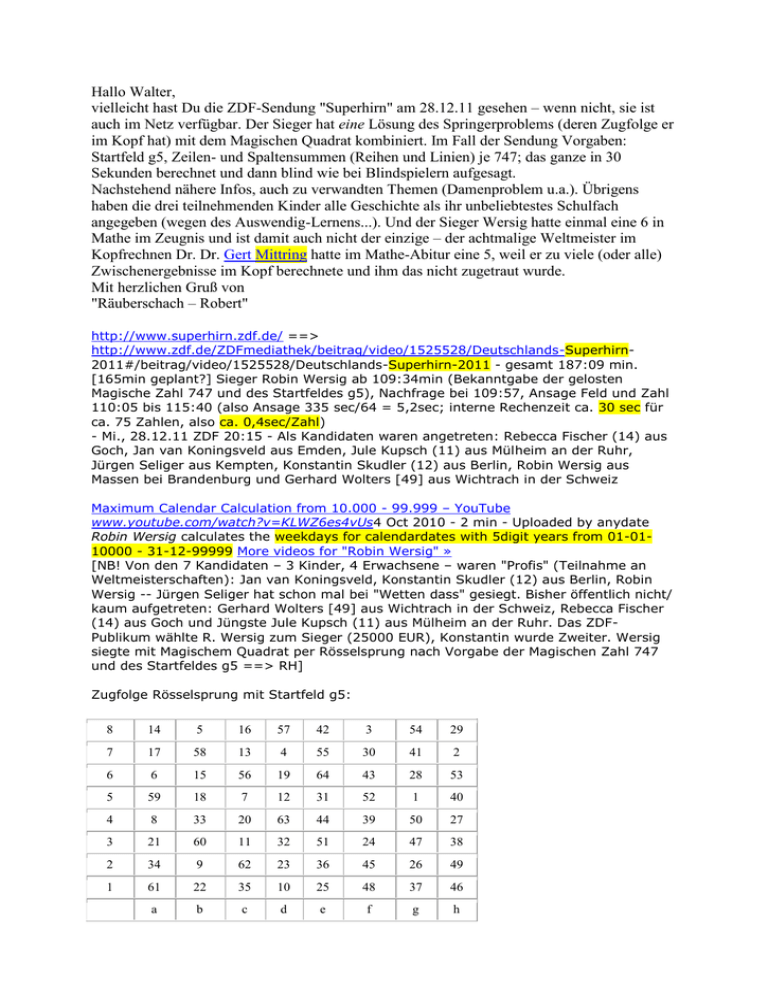
Hallo Walter,
vielleicht hast Du die ZDF-Sendung "Superhirn" am 28.12.11 gesehen – wenn nicht, sie ist
auch im Netz verfügbar. Der Sieger hat eine Lösung des Springerproblems (deren Zugfolge er
im Kopf hat) mit dem Magischen Quadrat kombiniert. Im Fall der Sendung Vorgaben:
Startfeld g5, Zeilen- und Spaltensummen (Reihen und Linien) je 747; das ganze in 30
Sekunden berechnet und dann blind wie bei Blindspielern aufgesagt.
Nachstehend nähere Infos, auch zu verwandten Themen (Damenproblem u.a.). Übrigens
haben die drei teilnehmenden Kinder alle Geschichte als ihr unbeliebtestes Schulfach
angegeben (wegen des Auswendig-Lernens...). Und der Sieger Wersig hatte einmal eine 6 in
Mathe im Zeugnis und ist damit auch nicht der einzige – der achtmalige Weltmeister im
Kopfrechnen Dr. Dr. Gert Mittring hatte im Mathe-Abitur eine 5, weil er zu viele (oder alle)
Zwischenergebnisse im Kopf berechnete und ihm das nicht zugetraut wurde.
Mit herzlichen Gruß von
"Räuberschach – Robert"
http://www.superhirn.zdf.de/ ==>
http://www.zdf.de/ZDFmediathek/beitrag/video/1525528/Deutschlands-Superhirn2011#/beitrag/video/1525528/Deutschlands-Superhirn-2011 - gesamt 187:09 min.
[165min geplant?] Sieger Robin Wersig ab 109:34min (Bekanntgabe der gelosten
Magische Zahl 747 und des Startfeldes g5), Nachfrage bei 109:57, Ansage Feld und Zahl
110:05 bis 115:40 (also Ansage 335 sec/64 = 5,2sec; interne Rechenzeit ca. 30 sec für
ca. 75 Zahlen, also ca. 0,4sec/Zahl)
- Mi., 28.12.11 ZDF 20:15 - Als Kandidaten waren angetreten: Rebecca Fischer (14) aus
Goch, Jan van Koningsveld aus Emden, Jule Kupsch (11) aus Mülheim an der Ruhr,
Jürgen Seliger aus Kempten, Konstantin Skudler (12) aus Berlin, Robin Wersig aus
Massen bei Brandenburg und Gerhard Wolters [49] aus Wichtrach in der Schweiz
Maximum Calendar Calculation from 10.000 - 99.999 – YouTube
www.youtube.com/watch?v=KLWZ6es4vUs4 Oct 2010 - 2 min - Uploaded by anydate
Robin Wersig calculates the weekdays for calendardates with 5digit years from 01-0110000 - 31-12-99999 More videos for "Robin Wersig" »
[NB! Von den 7 Kandidaten – 3 Kinder, 4 Erwachsene – waren "Profis" (Teilnahme an
Weltmeisterschaften): Jan van Koningsveld, Konstantin Skudler (12) aus Berlin, Robin
Wersig -- Jürgen Seliger hat schon mal bei "Wetten dass" gesiegt. Bisher öffentlich nicht/
kaum aufgetreten: Gerhard Wolters [49] aus Wichtrach in der Schweiz, Rebecca Fischer
(14) aus Goch und Jüngste Jule Kupsch (11) aus Mülheim an der Ruhr. Das ZDFPublikum wählte R. Wersig zum Sieger (25000 EUR), Konstantin wurde Zweiter. Wersig
siegte mit Magischem Quadrat per Rösselsprung nach Vorgabe der Magischen Zahl 747
und des Startfeldes g5 ==> RH]
Zugfolge Rösselsprung mit Startfeld g5:
8
14
5
16
57
42
3
54
29
7
17
58
13
4
55
30
41
2
6
6
15
56
19
64
43
28
53
5
59
18
7
12
31
52
1
40
4
8
33
20
63
44
39
50
27
3
21
60
11
32
51
24
47
38
2
34
9
62
23
36
45
26
49
1
61
22
35
10
25
48
37
46
a
b
c
d
e
f
g
h
Magisches Quadrat per Rösselsprung, magische Zahl (Reihen und Linien) 747; Startfeld
g5:
747
747
747
747
747
747
747
747
8
108
104
85
95
82
59
121
93
747
7
112
102
87
123
78
74
115
56
747
6
97
83
106
110
18
119
134
80
747
5
88
126
113
101
116
128
2
73
747
4
105
107
96
11
133
81
94
120
747
3
99
38
124
90
71
77
130
118
747
2
86
98
36
103
122
92
79
131
747
1
52
89
100
114
127
117
72
76
747
a
b
c
d
e
f
g
h
Zugfolge/ Feld/ Zahl, sortiert nach Zugfolge:
1
g5
2
2
h7
56
3
f8
59
4
d7
123
5
b8
104
6
a6
97
7
c5
113
8
a4
105
9
b2
98
10
d1
114
11
c3
124
12
d5
101
13
c7
87
14
a8
108
15
b6
83
16
c8
85
17
a7
112
18
b5
126
19
d6
110
20
c4
96
21
a3
99
22
b1
89
23
d2
103
24
f3
77
25
e1
127
26
g2
79
27
h4
120
28
g6
134
29
h8
93
30
f7
74
31
e5
116
32
d3
90
33
b4
107
34
a2
86
35
c1
100
36
e2
122
37
g1
72
38
h3
118
39
f4
81
40
h5
73
41
g7
115
42
e8
82
43
f6
119
44
e4
133
45
f2
92
46
h1
76
47
g3
130
48
f1
117
49
h2
131
50
g4
94
51
e3
71
52
f5
128
53
h6
80
54
g8
121
55
e7
78
56
c6
106
57
d8
95
58
b7
102
59
a5
88
60
b3
38
61
a1
52
62
c2
36
63
d4
11
64
e6
18
[NB! natürlich ist ein Trick dabei, nachfolgend ==> RH] Trick 747 - Wie man
Deutschlands Superhirn wird - Deutsche ... https://dmv.mathematik.de/.../1156-trick747-wie-man-deutschlands-...
vor 6 Tagen – ZDF-Publikum wählt Robin Wersig zum Superhirn 2011. ... Und tatsächlich
schaffte es der Kandidat Robin Wersig in der ZDF-Sendung, ein yyyy ...
https://dmv.mathematik.de/aktuell/aktuell/1156-trick-747-wie-man-deutschlandssuperhirn-wird.html DMV = Deutsche Mathematiker-Vereinigung
Startseite Aktuell/Presse Forum Veranstaltungen Aktivitäten Abiturpreis Mathemacher
Studium und Beruf Schulthemen
Die DMV Links zur Mathematik Publikationen Organisation Mitglieder Kontakt
Home Aktuell/Presse Aktuelles Trick 747 - Wie man Deutschlands Superhirn wird
Trick 747 - Wie man Deutschlands Superhirn wird
[Foto] ZDF-Publikum wählt Robin Wersig zum Superhirn 2011. (Quelle: ZDF Mediathek)
Am 28. Dezember 2011 suchte das ZDF in der gleichnamigen Sendung "Deutschlands
Superhirn 2011" und fand - Robert Wersig. Er könne als weltweit einziger das magische
Quadrat mit dem Rössel-Sprung lösen und das blind - so der 29jährige "Schnellrechner",
"Vizeweltmeister im Kalenderrechnen" und "Weltrekordhalter im Erstellen eines
Magischen Quadrats".
Im Vorfeld trauten ihm 69 Prozent der Zuschauer diese Leistung zu. Und tatsächlich
schaffte es der Kandidat Robin Wersig in der ZDF-Sendung, ein Schachbrett nur mit den
für das Pferd typischen Spielzügen im Geiste abzuschreiten - und dabei mit Zahlen so zu
füllen, dass jede der Zeilen- und Spaltensummen eine frei vorgegebene Zahl bildeten.
Dabei startete er von einem Feld, das die Zuschauer [NB! nein: Verona Pooth per
Dartpfeil RH] kurz zuvor bestimmt hatten.
"Das verstehe ich nicht", bekannte Talkmaster Jörg Pilawa in der Sendung schon bei der
Aufgabenstellung. Prompt wurde der sympathische Erzieher aus dem Brandenburgischen
Finsterwalde vom Publikum zu Deutschlands Superhirn 2011 gekürt.
Tatsächlich ist es unwahrscheinlich, dass Wersig "der einzige Mensch weltweit" ist, der
auf diesem Wege ein semimagisches Quadrat erzeugen kann, wie es in der Sendung
behauptet wurde. In Wirklichkeit lässt sich die Aufgabe nämlich mit relativ simplen Tricks
bewältigen. Der Kandidat muss nur im Vorfeld zwei Sachen auswendig lernen:
- Eine einzige Lösung für ein semimagisches Quadrat, zum Beispiel für Zeilensumme 0,
sowie
- eine Rundroute eines Springers, die über alle Felder des Schachbretts führt.
Egal, welches Feld auf dem Schachbrett nun vorgegeben wird, kann der Kandidat von
dort an alle Felder durchlaufen, indem er einfach der auswendig gelernten Rundroute
folgt. Die Zahlen zu berechnen ist ebenfalls einfach: Man zerlegt die vorgegebene
Zeilensumme in ein Vielfaches von 8 und einen Rest kleiner 8. Das Vielfache addiert man
zu jedem der Zahlenwerte in der auswendig gelernten Lösung, den Rest auf die Felder
einer der Diagonalen. In der Sendung war zum Beispiel die Zeilensumme 747 = 93*8 + 3
vorgegeben.
Mögliche auswendig gemerkte Lösung (Zeilen- und Spaltensummen sind 0)
12
11
-8
2
-11
-34
28
0
19
4
-5
12
6
-7
-41
6
-10
33
14
-55
5
-4
-6
10
20
3
31
-57
7
30
17
5
-82
-3
10
21
-15
-75
23
37
-22
29
34
-19
26
35
-12
-19
-1
24
22
41
-91
1
37
-17
-21
-37
-13
-20
27
25
38
-20
-8
-6
13
2
3
31
-57
7
2
30
17
8
-82
-3
10
21
-11
-15
-75
23
40
-22
29
34
-34
-19
26
35
-12
-16
-1
24
28
22
41
-91
1
37
-14
-21
0
-37
-13
-20
27
25
38
-17
85
87
106
113
96
124
36
100
95
123
110
101
11
90
103
114
82
78
18
116
133
71
122
127
59
74
119
128
81
77
92
117
121
115
134
2
94
130
79
72
93
56
80
73
120
118
131
76
eine Diagonale +3,
15
19
4
-5
12
6
-7
-41
11
9
-10
33
14
-55
5
-4
alle Felder +93,
108
112
97
88
105
99
86
52
104
102
83
126
107
38
98
89
und man hat die Lösung aus der Sendung vor sich, die der Kandidat im Kopf entlang der
auswendig gelernten Springer-Route ablaufen musste. Die spezielle Lösung von Robin
Wersig kann man sich in der ZDF Mediathek angucken.Zum Artikel von Holger Dambeck
auf Spiegel Online (4.1.2012) [......]
ENDE https://dmv.mathematik.de/aktuell/aktuell/1156-trick-747-wie-man-deutschlandssuperhirn-wird.html
[NB! also alles ganz easy, für jedes beliebige Startfeld und jede beliebige ganze Zahl –
läge sie im Millionen-Bereich, würde er vielleicht ein paar Sekunden länger brauchen.
Seine interne Rechenzeit war also ca. 30 sec für ca. 75 Zahlen, also ca. 0,4sec/Zahl –
danach brauchte er "nur noch" wie Blind-(Simultan-) Schachspieler die Zahlen in der
richtigen Reihenfolge anzusagen.
Wersig (29 J.) fährt Einrad, liebt Zaubertricks, Jonglieren; er hatte übrigens mal eine 6 in
Mathematik im Zeugnis. Aber auch das ist nichts Besonderes, weil es mindestens
mehrere hochrangige Gedächtnissportler/ -rechner gibt, die zeitweise sehr schlechte
Mathe-Noten hatten. Darüber ggf. mehr auf Nachfrage. RH]
========
http://www.hoerzu.de/unterhaltung/aktuelles/deutschlands-superhirn-2011
[Foto] "Deutschlands Superhirn 2011": Moderator Jörg Pilawa und Kandidat Konstantin
Skudler. Der Schüler kann sich in 100 Sekunden die Reihenfolge von 100 Brautleuten
merken. - Foto © ZDF / Max Kohr
Jörg Pilawa Deutschlands Superhirn 2011 Artikel vom 28. Dezember 2011
Manchmal bleibt nur Staunen: Da kommt ein zwölfjähriger Berliner und merkt sich
spielend mehr als 500 Zahlen in 30 Minuten. Selbstzweifel? Von wegen! Vor laufender
Kamera will Konstantin Skudler jetzt sogar sechs Konkurrenten mit seinen
außergewöhnlichen Fähigkeiten schlagen. "Deutschlands Superhirn 2011" heißt die neue
ZDF-Show (siehe TV-Tipp rechts), in der Jörg Pilawa erstaunliche Hirnleistungen
präsentiert – eine Art Casting für Genies.
Was sind das für Menschen, die das Zeug zum Superhirn haben? Zerstreute
Kopfakrobaten? Und welche Geheimnisse stecken hinter ihrem Können? Moderator Jörg
Pilawa wollte es genau wissen und besuchte Kandidaten zu Hause. Ein Unternehmen mit
Aha-Effekt: "Da kommt man in eine ganz normale Familie und trifft auf einen Jungen mit
Justin-Bieber-Frisur, der mitten im Leben steht, Pizza mag und einfach nur Spaß an
Gedächtnisübungen hat", erinnert sich Pilawa an seine erste Begegnung mit Konstantin
Skudler. Dieser Spaß führt allerdings zu sensationellen Erfolgen.
Die Kandidaten von "Deutschlands Superhirn 2011"
Wer das Superhirn werden will, muss viele Herausforderungen meistern.
1. Konstantin Skudler (12)
Der Junge aus Berlin mit dem Supergedächtnis. Sein Talent: "Ich kann mir in 100
Sekunden die Reihenfolge von 100 Brautleuten merken." Beruf: Schüler.
2. Gerhard Wolters (48)
Der Mann mit dem Supergehör. Sein Talent: "Ich kann bei einem Sinfonieorchester
exakt heraushören, welche Musiker gerade nicht mitspielen." Beruf: DiplomMusikpädagoge.
3. Jan van Koningsveld (41)
Der Geschwindigkeitsmesser. Sein Talent: "Ich bin eine menschliche Radarfalle und
kann im Kopf die Geschwindigkeit fahrender Autos berechnen." Beruf:
Industriekaufmann.
4. Jule Kupsch (11)
Meisterin des perfekten Gesichter-Erkennens. Ihr Talent: "Ich habe von eintausend
Babys alle Gesichter, Namen und Geburtsdaten im Kopf." Beruf: Schülerin.
5. Rebecca Fischer (13)
Die Gedächtniskünstlerin. Ihr Talent: "Ich kenne das komplette Fernstreckennetz der
Deutschen Bahn und auch alle zugehörigen Bahnhöfe auswendig." Beruf: Schülerin.
6. Robin Wersig (29)
Das Mathematikgenie. Sein Talent: "Ich bin der Superkopfrechner und löse das
Magische Quadrat mit dem Rösselsprung blind." Beruf: Erzieher.
7. Jürgen Seliger (39)
Der Mann mit dem fotografischen Gedächtnis. Sein Talent: "Ich erkenne 101 Dalmatiner
nur an einem kleinen Fellausschnitt.“ Beruf: Angestellter einer Holzbau-Softwarefirma.
Bei Weltmeisterschaften räumt Konstantin Skudler alles ab. Er hält acht Weltrekorde,
kein Mensch in seinem Alter kann sich so viele Zahlen, Wörter, Bilder, Vokabeln oder
Geschichtsdaten merken. In seinem Zimmer ist kaum noch Platz für die vielen Pokale, die
er schon gewonnen hat. Dass Konstantin mehr kann als andere , merkten seine Eltern,
als sie mit dem damals Dreijährigen ins Schwimmbad gingen. In der Umkleidekabine
lernte der Knirps die Reihenfolge der Zahlen an den Schränken. Schon mit fünf Jahren
wurde der Hochbegabte mit dem Intelligenzquotienten 140 eingeschult – gleich in die 2.
Klasse. Jetzt geht er in die 9. Klasse, genau wie seine zwei Jahre ältere Schwester
Friederike. Die beiden sind ein Herz und eine Seele, neidisch auf ihn ist Friederike nicht.
Die Familie geht angenehm gelassen mit Konstantins Hochbegabung um. Er besucht ein
normales Gymnasium, wird aber vielfältig gefördert. Und so merkt sich das Wunderkind
nicht nur unfassbar lange Zahlenreihen, sondern spielt auch Schach, Tischtennis und
Klavier, singt und puzzelt, ist Fußball- und Formel-1-Fan [NB! will Rennfahrer werden?!
RH]. Sein liebstes Hobby aber ist Karate. Zum Training nimmt er Jörg Pilawa mit. Der
TV-Star kommt ins Schwitzen, als ihn Konstantin in den Würgegriff nimmt und mit einem
gekonnten Trick auf die Matte wirft.
Superhirn: ohne Fleiss kein Preis
Der Zwölfjährige trägt den blauen Gürtel, das ist die fünfte Stufe beim Karate. Konstantin
ist ehrgeizig. Was er anpackt, macht er gut. "Ich will mich immer weiter verbessern",
sagt er. Auch beim Gedächtnissport. In der ZDF-Show wagt er deshalb eine knifflige
Herausforderung: Der junge Berliner will sich in 100 Sekunden die Reihenfolge von 100
Brautleuten merken. Schafft so etwas nur ein Superhirn? "Wie bei den meisten
Höchstleistungen steckt eine Kombination aus Begabung und Training dahinter“,
erklärt Prof. Tobias Bonhoeffer vom Münchner Max-Planck-Institut für Neurobiologie.
"Das ist ähnlich wie beim Sport. Intensives Basketballtraining reicht sicherlich nicht aus,
um ein zweiter Dirk Nowitzki zu werden. Andererseits könnte Nowitzki nur mit Begabung
allein nicht so überragend spielen." Erst die Formel "Talent plus Fleiß" bringt den großen
Erfolg. Und wer nicht so begabt ist? Der kann sich durch Üben zumindest verbessern – es
muss ja nicht gleich ein WM-Titel sein.
Prof. Bonhoeffer, der Jörg Pilawa in der Show als Experte begleitet: "Das gilt für alle
Hirnleistungen, also auch für das, was in der Sendung präsentiert wird." Bei Training und
Tricks setzen Superhirne auf bewährte Strategien. "Dazu gehört die sogenannte LociMethode", sagt Neurobiologe Bonhoeffer. "Man assoziiert vertraute Orte mit neuen
Gedächtnisinhalten, die man sich auf diese Weise besser merken kann."
Auch Wunderkind Konstantin baut sich solche Eselsbrücken. Zunächst verknüpft er
Zahlen oder Fakten mit Bildern. Die platziert er dann entlang bekannter Routen. Solche
Wege führen durch Haus und Garten, aber auch bei den Großeltern und in
Ferienwohnungen hat er seine Gedächtnisstützen. Die Methode kann jeder beim
Einkaufszettel nutzen: Auf dem Sessel liegt die Erdbeermarmelade (weil der Sessel rot
ist), auf dem Fernsehgerät die Zahnpasta (wegen der TV-Werbung). Wer in Gedanken die
Route abschreitet, kann sich besser erinnern. Andere Eselsbrücken helfen, wenn man
sich etwa PIN-Codes der Kreditkarten merken will.
Gedächtnissportler stellen sich die Zahlen bildlich vor: Die Null wird zum Ei, die Fünf
zur Hand, die Zwei zum Schwan. Jetzt verknüpft man diese Bilder mit einer
fantasievollen Geschichte. "502" wäre: Die Hand greift zum Ei, das der Schwan gelegt
hat. "Assoziationen helfen sehr viel", sagt Prof. Bonhoeffer, der sich in seinen
Forschungen seit Jahren mit Lernen und Gedächtnis beschäftigt. "Wir verbinden neue
Informationen mit etwas, was wir sowieso wissen."
Gedächtnistraining: Spaß muss sein
Loci-Methode, Zahlen-Assoziationen – das klingt nach Arbeit. Doch Superhirne schreckt
das nicht. Sie haben eine besondere Eigenschaft: Begeisterung! Das spürt man bei
Konstantin Skudler. Was fasziniert ihn so am Gedächtnissport? "Keine Ahnung",
antwortet der Berliner, "es macht mir einfach Spaß." Trotz der starken Konkurrenz ist er
siegessicher – obwohl er nur wenige Minuten pro Tag intensiv übt. "Den Titel des
Trainingsweltmeisters wird Konstantin nie gewinnen", lästert sein Vater. "Na und",
kontert der Sohn. "Ich habe ja auch noch Besseres zu tun."
Demnächst steht ein Konzertauftritt auf seinem Programm: Konstantin übt ein Stück von
Robert Schumann auf dem Klavier. Wie immer spielt er es auswendig. Vielleicht reicht es
ja trotz Trainingsrückstands für den Titel "Superhirn 2011". Darüber entscheiden die
Zuschauer im Studio. Eine prominente Jury begleitet den Wettkampf der Genies – und
trainiert dabei gleichzeitig die eigenen grauen Zellen. Dafür bringen die Kandidaten den
Stars knifflige Aufgaben mit, die sie in der Show meistern sollen. Genau der richtige Weg.
"Wir können unser Gedächtnis auf Zack halten, wenn wir geistig aktiv sind und uns
ständig fordern", sagt Prof. Tobias Bonhoeffer. "Eine Wunderdroge fürs Gehirn hat die
Forschung bislang nicht entdeckt."
Als legales Doping für den Kopf gelten immerhin fünf Strategien:
1. Bewegung
Sport verbessert die Durchblutung des Gehirns und aktiviert auch Regionen, die für das
Gedächtnis zuständig sind. Bewährt haben sich regelmäßiger Ausdauersport wie Laufen
und Radfahren, aber auch Wandern.
2. Üben
Das Gehirn muss gefordert werden, damit neue Verknüpfungen zwischen den Zellen
wachsen. Mit Strategiespielen wie etwa Schach oder schweren Denkaufgaben gelingt das.
Immer nur Kreuzworträtsel lösen reicht nicht.
3. Tanzen
Ausdauer, Koordination, schnelle Reaktionen – all das erfordert geistige Hochleistung und
ist deshalb so effektiv.
4. Soziale Kontakte
Bleiben Anreize aus, bilden sich Verknüpfungen im Gehirn zurück. Das Zusammensein
mit anderen bringt jedoch neue Anregungen, wirkt sich so positiv auf Denkvermögen und
Gedächtnis aus.
5. Ernährung
Als wichtigster Energielieferant für das Gehirn gilt Glukose. Ideal sind Kohlenhydrate aus
Vollkornprodukten, Nudeln, Obst und Gemüse. Ebenfalls wichtig: ausreichend Flüssigkeit!
Weil mit der Zeit die Konzentration nachlässt, bringt zu langes Gehirntraining jedoch
nichts. Das weiß auch Jörg Pilawa, der sich für seine Sendung intensiv mit dem Thema
Hirnforschung beschäftigt hat: "Entscheidend für den Erfolg sind vor allem die Motivation
und der Wille. Konstantin ist ein gutes Beispiel dafür." Der hat über 700 Routen angelegt,
genug, um sich mehr als 4200 Zahlen zu merken: "Das reicht erst mal." Autor: Thomas
Kunze / Kai Riedemann
[NB! KASTEN Weitere Infos Jörg Pilawa bei Wikipedia Homepage "Rette die Million!"
Gedächtnisweltmeisterin Christiane Stenger Tipps für Gedächtnistraining | | RH]
ENDE http://www.hoerzu.de/unterhaltung/aktuelles/deutschlands-superhirn-2011 [NB!
5.1.12 yyyy RH]
[NB! Folgendes als "Nachschlag", weil Priyanshi Somani alle erwachsenen Konkurrenten
inkl. Wersig an die Wand gerechnet hat. Das ist doch was, von einer Elfjährigen
geschlagen zu werden! Aber das haben einst die Gegner der Polgar-Sisters auch
wegstecken müssen. RH]
Elfjährige ist schneller als ein Taschenrechner Die Zeit vom 8. Juni 2010
http://www.zeit.de/wissen/2010-06/rechnen-wm-somani
Rechen-WM Elfjährige ist schneller als ein Taschenrechner
Priyanshi Somani ist erst elf und doch schon ein Mathematikgenie. Nun kann sich die
kleine Inderin gar Weltmeisterin im Kopfrechnen nennen.
Wie viel ist 12.364.953 mal 24.637.443? Priyanshi Somani könnte das Ergebnis im
Handumdrehen nennen, und zwar ohne technische Hilfsmittel. Denn die elfjährige Inderin
ist ein echtes Mathematiktalent und nun die neue Weltmeisterin im Kopfrechnen. In
Magdeburg setzte sich die Inderin in der Gesamtwertung gegen 37 Teilnehmer aus 16
Ländern durch. Vizeweltmeister wurde der Spanier Marc Jornet Sanz, auf Platz drei kam
sein Landsmann und Titelverteidiger Alberto Coto.
Somani war die jüngste Bewerberin um den zum vierten Mal vergebenen Titel. Der
älteste Teilnehmer war 61 Jahre alt. Der einzige Behelf der Rechengenies war ihr Kopf.
Sie addierten zum Beispiel zehn zehnstellige Zahlen in rasanter Geschwindigkeit,
multiplizierten achtstellige Zahlen oder zogen die Wurzel aus langen Zahlen.
Während bei der offiziellen Weltmeisterschaft am Sonntag keine Zuschauer erlaubt
waren, konnte die Öffentlichkeit am Montag Kostproben der beinahe an Zauberei
grenzenden Rechenkünste bekommen. Arturo Mendoza Huertas aus Peru warf etwa nur
einen kurzen Blick auf eine lange Zahlenkolonne und schon konnte er die richtige Summe
dieser Zahlen nennen – während ein Zuschauer noch dabei war, die Zahlen in einen
Taschenrechner einzutippen. Diese Maschine sei "kein würdiger Gegner" mehr, meinte
schmunzelnd Ralf Laue, Erfinder der Weltmeisterschaft im Kopfrechnen und
Mathematiker an der Universität Leipzig.
Doch auch die deutschen Vertreter schlugen sich achtbar. Robin Wersig aus dem
brandenburgischen Finsterwalde wurde Vizeweltmeister im Kalenderrechnen, weil er es
schaffte, in nur einer Minute insgesamt 47 Daten die richtigen Wochentage zuzuordnen.
Jan van Koningsveld aus dem niedersächsischen Emden landete auf Platz drei in dieser
Disziplin, Weltmeister wurde Yusnier Viera aus Kuba.
Elfjährige Inderin Weltmeisterin im Kopfrechnen
www.klamm.de/partner/unter_news.php?l_id... - Translate this page
7. Juni 2010 – Robin Wersig aus dem brandenburgischen Finsterwalde, schaffte es zum
Beispiel, in einer Minute 47 Sekunden verschiedene Tage richtig ...
http://www.klamm.de/partner/unter_news.php?l_id=26&news_id=237379
Elfjährige Inderin Weltmeisterin im Kopfrechnen
MAGDEBURG (dpa/cf) - Ein elfjähriges Mädchen aus Indien ist Weltmeisterin im
Kopfrechnen.
Priyanshi Somani war die jüngste Teilnehmerin der vierten Weltmeisterschaft im
Kopfrechnen, die am Sonntag und Montag [6./7.6.2010] in Magdeburg veranstaltet
wurde.
Sie setzte sich gegen 37 Teilnehmer aus 16 Ländern durch - der älteste war 61 Jahre alt.
Die flinken Rechner addierten zum Beispiel zehn zehnstellige Zahlen in rasanter
Geschwindigkeit oder multiplizierten achtstellige Zahlen.
Beim Kalenderrechnen wussten die Rechenkünstler in Windeseile, auf welchen
Wochentag ein bestimmtes Datum fiel. Robin Wersig aus dem brandenburgischen
Finsterwalde, schaffte es zum Beispiel, in einer Minute 47 Sekunden verschiedene Tage
richtig zuzuordnen. Er wurde Vizeweltmeister in dieser Disziplin. Auf den ersten Platz im
Kalenderrechnen kam Yusnier Viera aus Kuba.
Die zuletzt veranstaltete Weltmeisterschaft im Kopfrechnen fand vor zwei Jahren in
Leipzig statt. Somani löste am Montag den bis dahin amtierenden Weltmeister Alberto
Coto aus Spanien ab. Die WM gehört zum Wissenschaftssommer 2010.
Panorama/Leben
[dnews.de] · 07.06.2010 · 19:43 Uhr · 211 Views [0 Kommentare]
ENDE http://www.klamm.de/partner/unter_news.php?l_id=26&news_id=237379 [NB!
4.1.12 RH]
======
LÖSUNGEN FÜR DAS DAMENPROBLEM
==> http://en.wikipedia.org/wiki/Eight_queens_puzzle
Alle 12 Lösungen, sortiert (L= Lösung Nr. im engl. wiki-Artikel; "7 a2-Lösungen" = es
gibt 7 eindeutige Lösungen mit Startfeld a2, die nicht durch Drehen/ Spiegeln ineinander
überführbar sind; "L11b" = diese Lösung geht durch Drehen/ Spiegeln in L11 über,
stillschweigend =L11a.):
L2:a1 b7 c4 d6 e8 f2 g5 h3;
L3:a1 b7 c5 d8 e2 f4 g6 h3; (2 a1-Lösungen)
L1:a2 b4 c6 d8 e3 f1 g7 h5;
L4:a2 b5 c7 d1 e3 f8 g6 h4;
L5:a2 b5 c7 d4 e1 f8 g6 h3;
L6:a2 b6 c1 d7 e4 f8 g3 h5;
L7:a2 b6 c8 d3 e1 f4 g7 h5;
L8:a2 b7 c3 d6 e8 f5 g1 h4;
L9:a2 b7 c5 d8 e1 f4 g6 h3; (7 a2-Lösungen)
L:a2 b8 c6 d1 e3 f5 g7 h4 (= L8b);
L:a3 b1 c7 d5 e8 f2 g4 h6 (= L6b);
L12:a3 b5 c2 d8 e1 f7 g4 h6 (punktsymmetrisch);
L:a3 b5 c2 d8 e6 f4 g7 h1 (= L2b);
L10:a3 b5 c8 d4 e1 f7 g2 h6;
L11:a3 b6 c2 d5 e8 f1 g7 h4; (3 a3-Lösungen)
L:a3 b6 c2 d7 e1 f4 g8 h5 (= L4b);
L:a3 b6 c2 d7 e5 f1 g8 h4 (= L5b);
L:a3 b6 c4 d1 e8 f5 g7 h2 (= L9b);
L:a3 b6 c8 d1 e5 f7 g2 h4 (= L11b);
L:a3 b6 c8 d2 e4 f1 g7 h5 (= L10b);
L:a3 b7 c2 d8 e6 f4 g1 h5 (= L7b);
L:a4 b1 c5 d8 e2 f7 g3 h6 (= L4c);
L:a4 b2 c5 d8 e6 f1 g3 h7 (= L7c);
L:a4 b2 c8 d6 e1 f3 g5 h7 (= L1b);
L:a4 b7 c3 d8 e2 f5 g1 h6 (= L1c);
L:a4-Lösungen: weitere....
L:a5 .... => a4-Lösungen
Wegen der 4 Symmetrieachsen – ohne Rücksicht auf die Feldfarbe – kann jede
eindeutige Lösung L1 bis L11 durch Drehen/ Spiegeln achtmal erzeugt werden, bis auf
die punktsymmetrische Lösung L12, die es nur viermal gibt: 12*8 -4 = 92 Lösungen.
vgl. auch: http://de.wikipedia.org/wiki/Damenproblem
======
LÖSUNGEN FÜR DAS SPRINGERPROBLEM
Anzahl geschlossener Touren [Bearbeiten]
Auf einem 6x6-Brett gibt es 9862 [NB! 1658/8 = 207,25 RH] und auf einem 8x8-Brett
13267364410532 ungerichtete geschlossene Touren.[3] [NB! "ungerichtet" = ohne
Berücksichtigung der Laufrichtung - 13267364410532/8 = 1658 420 551 316,5 => ≥
1658e9 = 1,6 Mio Mio (!!) eindeutige geschlossene Lösungen, die durch Drehen oder
Spiegeln nicht ineinander überführbar sind RH].
Diese Seite wurde zuletzt am 29. Dezember 2011 um 01:31 Uhr geändert.
ENDE http://de.wikipedia.org/wiki/Springerproblem
--------On an 8 × 8 board, there are exactly 26,534,728,821,064 directed closed tours (i.e. two
tours along the same path that travel in opposite directions are counted separately, as
are rotations and reflections).[4][5][6] [NB! 26534728821064/2 = 13267364410532 =
13e12 undirected; 13267364410532/8 ==> ≥ 1658420551316,5 = 1658e9 = 1,6 Mio
Mio (!!) eindeutige geschlossene Lösungen, die durch Drehen oder Spiegeln nicht
ineinander überführbar sind RH] The number of undirected closed tours is half this
number, since every tour can be traced in reverse. There are 9,862 undirected closed
tours on a 6 × 6 board.[7] [NB! 9862/8 = 1232,75 RH]. last modified on 15 December
2011 at 10:30.
ENDE http://en.wikipedia.org/wiki/Knight%27s_tour