Externe Unternehmensrechnung

www.uni-graz.at/iufwww/EU
www.wiwi.uni-frankfurt.de/Professoren/Ewert/EU
 Wagenhofer/Ewert 2002.
Alle Rechte vorbehalten.
Publizität und
Publizitätsanreize
7.1
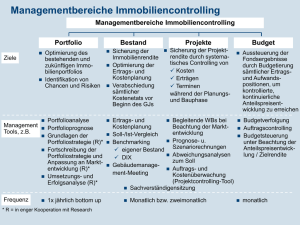
Ziele

Gesetzliche und freiwillige Publizität

Anreize zur Informationsbekanntgabe

Publizitätspolitiken und Bildung skeptischer
Erwartungen in einem Gleichgewicht:
Unraveling-Prinzip

Auswirkungen von
 Publizitätskosten
 Unsicherheit über den Erhalt von Information
 Konkurrenzgefahr
7.2
Gesetzliche und
freiwillige Publizität


7.3
Publizität ist wesentlicher Bestandteil zur
Erfüllung der Funktionen der externen
Unternehmensrechnung
Finanzberichterstattung
 Gesetzliche Regeln zur
Offenlegung
 Jahresabschlüsse und
Lageberichte
 Zwischenberichte
 Börseprospekte
 Ad-hoc-Mitteilungen
 Freiwillige Information
 Nicht geforderte Berichte
 Anreicherung mit
Zusatzinformationen
 Jahresabschlüsse nach
international anerkannten
Rechnungslegungsvorschriften
 Value Reporting
 Umweltberichterstattung
 Sozialberichterstattung
Rechtliche
Publizitätsvorschriften (1)

Differenzierungskriterien zur Offenlegung






Rechtsform
Größe
Einzel- oder Konzernabschluss
Branche
Börsennotierung
Erforderliche Qualität
 Prüfungspflicht
 Jahresabschluss und Lagebericht
 Börsenprospekt
 Keine Prüfungspflicht
 Zwischenbericht
 Ad-hoc-Meldungen
7.4
Rechtliche
Publizitätsvorschriften (2)

Begründung rechtlicher Regelungen
 Annahme: Unternehmen müssen verpflichtet werden,
Informationen zu geben
 Frühe Argumente: Zusammenhang mit beschränkter
Haftung, Schutz von Kleinaktionären, öffentliches Interesse
 Heute Informationsbedürfnisse von Kapitalmarktteilnehmern
im Vordergrund
 Internationale Standards (IFRS, US-GAAP) als Vorbild

Analyse der Publizitätspolitik
 Vergleichsgröße zur Beurteilung der Auswirkungen
rechtlicher Publizitätsvorschriften
 Beurteilung der Frage, ob nicht der (Kapital-)Markt
vergleichbare Ergebnisse erzielen kann
7.5
Unraveling-Prinzip
Unternehmen
7.6
Gibt Information
bekannt
Adressat
Trifft Entscheidung
Auswirkung auf
Unternehmen

Annahmen
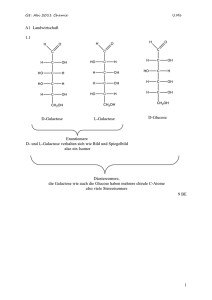
 Tatsächlicher Wert p eines Unternehmens unsicher
 A priori Erwartungswert E[p]
 Unternehmen besitzt wertrelevante Information y,
a priori gleichverteilt im Intervall Y = [0, 1]
 A posteriori Erwartungswert P = E[py] = y
 Wahrheitsgetreue oder keine Informationsweitergabe

Unternehmen maximiert P
Unraveling-Prinzip
Ausweisstrategie

Ausweisstrategie
m( y) 






y falls ausgewiesen wird
{} falls nicht ausgewiesen wird
Einteilung von Y
 Ausweisbereich D = {ym(y) = y}
 Nichtausweisbereich N = {ym(y) = {}}
 Keine Überschneidung der Teilmengen
N  D = Y und N  D = {}
7.7
Unraveling-Prinzip
Intuition

Iterativer Prozess
 Angenommen, Marktwert ist
P = E[p] = E y  Ep [p y] = 0,5
Ausweis von y > P = 0,5
 Aber: Markt erkennt dies
Marktpreisrevision bei Nichtausweis von y  [0; 0,5]
P = E[py  [0; 0,5] ] = 0,25
 Unternehmen antizipiert dies
Ausweis von y > P = 0,25
 Neuerlich Marktpreisrevision zu P = 0,125
 usw ...
solange bis Gleichgewichtszustand erreicht ist
entspricht Gleichgewicht
7.8
Unraveling-Prinzip
Gleichgewicht

Gleichgewicht besteht aus
 Ausweisstrategie m*(y), die für jede Information y Marktpreis
P maximiert
 Rationale Erwartungen der Marktteilnehmer, die für jedes
beobachtete m Marktpreis P festlegen, der tatsächlich
zugrunde liegenden Informationen entspricht

Gleichgewicht definiert durch Nichtausweisbereich
N = {yy  E[py  N]}
 Erwartungswert von Elementen einer Menge immer kleiner
als das größte Element – N nie mehr als ein Element
 Im Gleichgewicht Annahme der ungünstigsten Situation bei
Nichtausweis
 Gleichgewicht: Vollständiger Ausweis, N = {0}
7.9
Unraveling-Prinzip
Diskussion

Nur ein Gleichgewicht, wenn das Unternehmen
wertrelevante Informationen besitzt und die
Marktteilnehmer das wissen
 Ausweisstrategie: Ausweis jeder Information
 Skeptische Erwartungen bei Nichtausweis
„Keine Antwort ist auch eine Antwort.“

Umfassende Gültigkeit
 Unabhängigkeit von der Art der Information
 Unabhängigkeit von zugrunde liegenden
Wahrscheinlichkeitsverteilungen
 Nur monotone Zielerreichung erforderlich

Aber: Keine Bestätigung in der Praxis
7.10
Exkurs
„Lemons“ principle (Akerlof)

Zusammenbruch des Gebrauchtwagenmarktes







Besitzer besser informiert, Versuch Mängel zu vertuschen
Käufer setzt Durchschnittspreis
„Gute“ Wagen nicht mehr angeboten, da mehr wert
Reduktion des Durchschnittspreises
Weitere Wagen nicht mehr angeboten, weitere Reduktion
Resultat: nur Gebrauchtwagen der schlechtesten Qualität
(„lemons“) zu dem ihnen angemessenen Preis angeboten
Gründe, warum dennoch ein
Gebrauchtwagenmarkt existiert




Weitere Präferenzen (zB neues Modell)
Prüfung durch unabhängige Fachkundige,
Garantien, Rückgaberechte
Reputation der Autohersteller
7.11
Direkte Kosten der Publizität (1)

Direkte Kosten
 Erstellung der Publikation
 Veröffentlichung
 Verifikation, zB Abschlussprüfung

Annahmen
 Bei Ausweis konstante Kosten k > 0
 Y = [0, 1]
 P = E[py] = y

Gleichgewichtsbedingung
N = {yy – k  E[py  N]} = [0, y1]
y1 – k = E p y [0, y1] = y1/2 und


y1 = min {2k, 1}
7.12
Direkte Kosten der Publizität (2)
1
Marktpreis P
Wert ohne
Kosten der
Publikation
Überbewertete
Unternehmen
Unterbewertete
Unternehmen
y1 – k
0
Kosten der
Publikation k
Nichtausweis
Ausweis
y1 = 2k
1
Information y
7.13
Verpflichtung zu Ausweisstrategie

Glaubwürdige Verpflichtungsstrategie





Muss vor Kenntnis der Information y erfolgen
Verpflichtung zu vollständigem Ausweis oder Nichtausweis
Direkte Kosten k verringern Unternehmenswert
Ex ante keine Änderung des Erwartungswertes
Ergebnis
 Kosten 1k bei Verpflichtung zu vollständigem Ausweis
 Verpflichtung zu vollständigem Nichtausweis günstig, da
keine Publizitätskosten
 Erwartete Publizitätskosten im Gleichgewicht kF(D)
 In diesem Fall negativer gesamtwirtschaftlicher Effekt bei
rechtlicher Publizitätsregelung
7.14
Unsicherheit über den Erhalt
von Information

7.15
Marktteilnehmer unsicher, ob Unternehmen
Information y besitzt
 Gewinnung von Informationen mit Kosten verbunden
 Erwartungen der Marktteilnehmer über die
Wahrscheinlichkeit f , dass keine Information vorliegt
Ausweis
(1–f)F(D)
kein Ausweis
(1–f)F(N)
kein Ausweis
f
Information
keine
Information
Gleichgewicht bei unsicherem
Erhalt von Informationen (1)

Preisbildung bei Nichtausweis durch rationale
Erwartungen der Marktteilnehmer
PN 
f  E[p y Y ]  (1f ) F ( N )  E[p y  N ]
f  (1f ) F ( N )
 Annahme: Information nicht produktiv
(intern keine bessere Entscheidungsgrundlage)

Ausweis nur bei Besitz der Information möglich
 Ausweis dann, wenn y > PN
 Nichtausweisbereich ein Intervall von ungünstigen
Information N = [0, y1] mit indifferenten Grenzwert y1
7.16
Gleichgewicht bei unsicherem
Erhalt von Informationen (2)

Erfolgreiches Verheimlichen von ungünstigen
Informationen möglich
 Grenzfälle:
 f  0: Praktisch mit Sicherheit Information vorhanden,
Erwartungen in Richtung y = 0 und PN = 0
 f  1: Fast mit Sicherheit keine Information da,
a priori Erwartungen PN = 0,5
 Nichtausweisbereich N steigt mit f

Resultat
 Unternehmen mit nicht ausgewiesenen Informationen
überbewertet, da PN > y  N
 Unternehmen ohne Information unterbewertet, da PN < E[y]
7.17
Timing des Ausweises (1)
7.18
Verzögerte Publikation ungünstiger Informationen
beobachtbar

 Annahme einer steigenden Wahrscheinlichkeit für den Besitz
von Informationen im Zeitablauf bei Periodenlänge 1
f(t) = 1 – t
Preis bei Nichtausweis
0,5
0
1
Wahrscheinlichkeit, dass keine Information vorliegt
Zeitablauf
0
 Solange keine
Information: kein
Ausweis möglich
 Information y zum
Zeitpunkt t – sofortiger
Ausweis, wenn y > PN(t)
 Sonst verzögerter
Ausweis zum Zeitpunkt,
zu dem gilt y = PN(t)
Information über das
Nichtvorliegen von Information

7.19
Bekanntgabe des Nichtbesitzes von Information
 Keine Änderung bei nicht glaubwürdiger Bekanntgabe
 Änderung bei glaubwürdiger Bekanntgabe
 Im Gleichgewicht skeptische Erwartungen von PN = 0 und
deshalb vollständiger Ausweis
 P = y bei Information und (erzwungener) Bekanntgabe
 P = 0,5 bei Nichtbesitz von Information und Bekanntgabe
Schutzklauseln
Trotz Ausweisgebots müssen bestimmte Informationen, die „nach vernünftiger kaufmännischer
Beurteilung geeignet [sind], dem Unternehmen oder einem verbundenen Unternehmen einen
erheblichen Nachteil zuzufügen“ (so zB § 286 dHGB, § 241 öHGB), nicht bekannt gegeben werden.
Die Anwendung der Schutzklausel muss aber angegeben werden. Dadurch verliert die Schutzklausel
einen Großteil ihrer Wirkung, da intensive Nachforschungen von interessierten Adressaten die Folge
sein werden. Es besteht fast ein Anreiz für das Unternehmen, die Information trotz Anwendbarkeit der
Schutzklausel (freiwillig) bekannt zu geben und auf eine dahingehende Interpretation der Adressaten zu
hoffen, dass das Unternehmen der Information keine negative Bedeutung beimesse.
Bei Nichtausweis von Information, weil es das öffentliche Interesse erfordert (§ 286 Abs 1 dHGB, § 241
Abs 1 öHGB), darf die Anwendung der Schutzklausel nicht angegeben werden...
Effekte der Publizität
anderer Unternehmen (1)

Herdenverhalten von Unternehmen
 „Vorbildunternehmen“ prägen Erwartungshaltung über
Vorhandensein von Informationen
 Informationskorrelation der Unternehmen – Lernen aus der
Publikation anderer Unternehmen

Beispiel
 Zwei Unternehmen A und B: entweder haben beide oder
keines Information
 Informationen selbst im Intervall [0, 1] gleichverteilt und
unabhängig
 Folge: Weist ein Unternehmen aus, ist bekannt, dass auch das
andere Unternehmen die Information besitzt
und entsprechende Erwartungsrevision für nichtausweisendes
Unternehmen
7.20
Effekte der Publizität
anderer Unternehmen (2)

Gleichgewicht
 Ausweis entweder von beiden Unternehmen oder von keinem
 Wahrscheinlichkeit für Ausweis F(N)2 < F(N)
 Preiserwartung der Marktteilnehmer bei Nichtausweis
f  E[p y Y ]  (1f )  F ( N )2  E[p y  N ]
P 
f  (1f ) F ( N )2
N

Ergebnis
 P bei Nichtausweis steigt, da kleinerer, bedingter Mittelwert
E[py  N] weniger stark gewichtet
 Insgesamt mehr Ausweis, da Wahrscheinlichkeit 1 – F(N)2
größer als vorher (mit 1 – F(N))
 Bei nicht vollständiger Korrelation Effekte weniger stark
7.21
Konkurrenzsituation und
Ausweisverhalten

Publikation für alle grundsätzlich Interessierten
 Auch „feindliche“ Nutzung der Information
 Konkurrenz als wesentlichstes Hindernis für Publikation
 Mit Bekanntgabe einer Information verbundene
Konkurrenzgefahr sinkt im Zeitablauf
 Weniger Schutzklauseln bei internationalen Standards

Konkurrenzgefahr
 Latente Konkurrenzgefahr
Potenzieller Eindringling in den Markt
 Bestehende Konkurrenz
7.22
Latente Konkurrenzgefahr (1)

Annahmen




Maximierung des Marktpreises P
A priori gleichverteilte Information y  Y = [0, 1]
Bei Publikation Marktpreisänderung von P auf y
Information relevant für anderes Unternehmen
 Eindringen bei günstiger Information
 Kein Eindringen bei ungünstiger Information
 Gleicher Informationsstand für Markt und potenziellen
Eindringling

Potenzieller Eindringling
 Kosten K bei Eindringen
 zB Kosten zur Aufbereitung des Marktes, Anlaufkosten,
Vertragskosten und Informationskosten
 Eindringen bei E[py m(y)]  K
7.23
Latente Konkurrenzgefahr (2)

Strategie des potenziellen Konkurrenten
 g (m) = 0 bei Nichteindringen
 g (m) = 1 bei Eindringen
 0 < K < 1 wegen y  [0, 1]


7.24
g (m) 





0 falls E[p y m( y)]  K
1 falls E[p y m( y)]  K
Unternehmen: Kosten k bei Eindringen
Ziele des Unternehmens
 Verhindern des Eindringens: Ausweis ungünstiger Information
 Maximierung des Marktpreises: Ausweis günstiger Information

Gleichgewicht
N = {yy – g (y)k  E[py  N] – g (N)k}
Latente Konkurrenzgefahr
Beispiel (1)
K = 0,7; k = 0,5

Gleichgewichte
 Kein Gleichgewicht ohne Ausweis
 Bei vollständigem Nichtausweis würde Konkurrent nicht
eindringen, denn
E[py  [0, 1] ] = 0,5 < 0,7 = K
 Ausweis von Informationen y  [0,5, 0,7] bei P = 0,5
 Kein Eindringen, Marktpreis aber über 0,5
 Nichtausweisbereich im Gleichgewicht
N = [0, 0,4]  [0,7, 0,9]
 Ausweis durchschnittlich günstiger Informationen
y  [0,4, 0,7] und sehr günstiger Informationen y  [0,9, 1]
7.25
Latente Konkurrenzgefahr
Beispiel (2)
7.26
1
Marktpreis P
Konkurrent
dringt ein
Überbewertete
Unternehmen
Unterbewertete
Unternehmen
0,4
Ausweis
Nichtausweis
0
0,4
AusNichtausweis weis
0,7
0,9
1
Information y
Latente Konkurrenzgefahr
Beispiel (3)

7.27
Nash-Gleichgewicht
 Richtige Bewertung des Unternehmens durch den Markt bei
Nichtausweis


0,4 0,4   0,9  0,7   0,7  0,9  0,42  0,92  0,72
2
2  2

2
E[p y  N ] 
 0,4
0,4  0,2
(0,4  0)  (0,9  0,7)
 Kein Eindringen bei Nichtausweis, denn
E[py  N] = 0,4 < 0,7 = K
 Kein Anreiz zum Abweichen von Ausweisstrategie
 Wegen E[py  N] = 0,4 kein Ausweis von y kleiner gleich 0,4
 Ausweis von Informationen größer als 0,4 bis zu 0,7
 Wegen k = 0,5 kein Ausweis von y größer als 0,7 bis zu 0,9
 Wegen 0,9 – k = 0,4 Ausweis von Information größer 0,9
Vollausweisgleichgewicht bei
latenter Konkurrenzgefahr (1)

7.28
Gleichgewicht mit vollständigem Ausweis
Skeptische Erwartungen und Nichtausweisbereich N = {0}
Marktpreis P
1
0,7
Konkurrent
dringt ein
0,2
Ausweis
0
0,7
1
Information y
Vollausweisgleichgewicht bei
latenter Konkurrenzgefahr (2)

Skeptische Erwartungen, die vollständigen
Ausweis induzieren
min {0, K – k}
 „Worst case“: k > K – negativer Marktpreis (nach Kosten)

Teilausweisgleichgewicht jedenfalls vorteilhafter
für Unternehmen
 Marktpreis gleich hoch oder höher
 A priori Wahrscheinlichkeit des Eindringens bei
Teilausweis 10 %, bei vollständigem Ausweis 30 %

Verpflichtung zum Nichtausweis noch besser
 Aber nur, wenn Konkurrent dabei nicht eindringt
7.29
Ergebnis

A priori geringe Konkurrenzgefahr (hier K > 0,5)
 Weniger Ausweis bei Teilausweisgleichgewicht
 Weniger Ausweis bei Erhöhung der Konkurrenzgefahr im
Gleichgewicht mit nur einem Ausweisintervall D = [y1, K]

Hohe Konkurrenzgefahr (hier K < 0,5)
 Teilausweisgleichgewicht nur bei ganz bestimmten k
 Meist nur Vollausweisgleichgewicht
 Mehr Ausweis bei Erhöhung der Konkurrenzgefahr

Mehr Ausweis bei steigenden Kosten k bei K < 0,5
 Nur bei Teilausweisgleichgewicht weniger Ausweis

Weniger Ausweis bei steigendem k bei K > 0,5
 k irrelevant bei Gleichgewicht mit nur einem Ausweisintervall
7.30
Bestehende Konkurrenz

Analyse in einer Duopolsituation
 Information dient der Verbesserung der Preis- und
Mengenpolitik

Annahmen
 Zwei Unternehmen A (informiert) und B
 Homogene Produkte
 Lineare Preis-Absatz-Funktion p = a – (xA + xB)
mit a > 0 als Prohibitivpreis und Cournot-Konkurrenz
 Konstante für beide Unternehmen gleich hohe
Produktionskosten k und Fixkosten gleich null
 Gewinn
pi = (p – k)xi = (a – k – xA – xB)xi ( i = A, B)
 Information y  (a – k), wobei A Information y kennt und B
weiß, dass y in Y = [1, 2] gleichverteilt ist und A y besitzt
7.31
Anreize zum Ausweis bei
bestehender Konkurrenz

Interesse an möglichst hohen Unternehmenswert
 Günstige Information y > E[y]
 Günstige Marktsituation (a hoch) oder geringe Stückkosten k
 Produktionssteigerung wegen höherem Deckungsbeitrag
 Erhöhung der Produktionsmenge des Konkurrenten bei
Bekanntgabe von y
 Nachteilige Wirkung der Publikation von y
 Ungünstige Information y < E[y]
 Bei Nichtbekanntgabe der Information starke Verringerung
der eigenen Produktion
 Drosselung der Produktionsmenge des Konkurrenten bei
Bekanntgabe der Information
 Ausweis günstig
7.32
Bestehende Konkurrenz
Analyse (1)

Ermittlung des Marktgleichgewichts
 Bei Ausweis
 Optimale Produktionsmenge xA
 p A  y  2x  x  0 und x ( y)  y  xB
B
A
A
 xA
2



Simultanes Setzen der Mengen im Cournot-Gleichgewicht
Einsetzen von xB in Bestimmungleichung für xA
y  xA
y

y  xB
2
xA( y) 

und damit xA( y)  y
2
2
3
Gewinn im Gleichgewicht
2
 y
y
y
p A( xA( y), xB ( y), y)  y  2   
3 3 9



7.33
Bestehende Konkurrenz
Analyse (2)

7.34
Gewinn von Unternehmen A
p A( xA( y), xB ( y), y)   y  2 y   y  y

3 3
2
9
 p A  y  2x  x  0  x y  y  x y  x
B
B
A
A 
A 
 xA

Gewinn von A bei optimaler Aktion bei irgendeiner
gegebenen Produktionsmenge von B
p A  xA  y , xB, y    y  xA  y   xB  xA  y   xA  y 2

Analoge Geltung dieser Beziehung auch für den Fall des
Nichtausweises von Unternehmen A
Bestehende Konkurrenz
Analyse (3)
7.35
 Bei Nichtausweis
 Wahl der Produktionsmenge (xB(N)) auf Grund der
Erwartungen y  N
 Für informiertes Unternehmen wie bei Ausweis
y  xB ( N )
xA( y, N ) 
2
E[ y N ] xB ( N )
E[ y N ] E[ xA N ] E[ y N ]
2
xB ( N ) 

2
2
E[ y N ]
xB ( N ) 
3
E[ y N ]
y
E[ y N ]
y
3
xA( y, N ) 
 
2
2
6






E[ y N ] 
y
Gewinn bei Nichtausweis p A( xA( y, N ), xB ( N ), y)  
2
6 

2
Gleichgewicht bei
bestehender Konkurrenz

Ausweisentscheidung durch Vergleich der
Gewinne bei Ausweis und bei Nichtausweis
 Ausweis aller y, für die gilt:





2
E[ y N ] 
 y
y
p A( xA( y), xB ( y), y)    > 
 p A( xA( y, N ), xB ( N ), y)
2
6 
 3
2

y  y  E[ y N ] bzw y  E[ y N ]
3 2
6
 Nichtausweisbereich
N  { y y  E[ y N ]}

Vollständiger Ausweis einziges Gleichgewicht
 Im Gleichgewicht gilt N = {2}
 Bestehende Konkurrenz für sich keine Begründung für
weniger Ausweis (Unraveling-Prinzip!)
7.36
Bestehende Konkurrenzgefahr
und Kapitalbedarf (1)

Berücksichtigung des Kapitalmarktes
 Zuvor Orientierung am (intrinsischen) Unternehmenswert
 Unternehmen auch an aktuellem Marktpreis interessiert
 Zielkonflikt:
Unternehmenswertmaximierung
(Ausweis ungünstiger Informationen vorteilhaft) vs.
Marktpreismaximierung
(Ausweis ungünstiger Informationen nachteilig)

Eigenkapitalaufnahme über den Kapitalmarkt
 Interesse an möglichst hohem Unternehmenswert
 Kapital in Höhe von EK > 0 benötigt
 a als auszugebenden Anteil am Unternehmen
7.37
Bestehende Konkurrenzgefahr
und Kapitalbedarf (2)

Benötigtes Kapital
EK = aE[pAm]
 Wahrheitsgemäße Veröffentlichung m = y oder
m = {} bei Nichtveröffentlichung
 Im Gleichgewicht Interpretation von m = {} als y  N

Maximierung des verbleibenden
Unternehmenswertes als Ziel
max(1
a (m))p A( xA( y, m), xB (m), y)
m
a (m) 
EK
E p A ( xA ( y, m), xB (m), y m 
7.38
Bestehende Konkurrenzgefahr
und Kapitalbedarf (3)

Produktionsstrategien der beiden Unternehmen
sowie der Gewinn des Unternehmen A
xB (m)  E[ y m] und xA( y, m)  y  E[ y m]
3
2
6





E[
y
m
]
y

p A ( xA( y, m), xB (m), y)  
2
6 

2
Inhärenter Zielkonflikt deutlich
 Hoher verbleibender Anteil (1 – a) durch hohe y
 Verringerung des Gewinns pA durch Konkurrenzreaktion auf
günstige Information
 Umgekehrt bei ungünstigen Informationen
7.39
Bestehende Konkurrenz und
Kapitalbedarf  Gleichgewicht

IdR mehrere Gleichgewichte

Es kann Gleichgewichte geben, in denen nicht alle
Informationen veröffentlicht werden
 Voraussetzung: Ziele in etwa gleich wichtig
 Bei geringem Kapitalbedarf überwiegt die Furcht vor
Konkurrenzreaktion
 Unraveling im Gleichgewicht
 Bei erforderlicher Aufnahme von viel Kapital Fokussierung
auf a
 Auch vollständiger Ausweis
7.40
Bestehende Konkurrenzgefahr und
Kapitalbedarf – Beispiel (1)

1. Vollständiger Ausweis mit N = {2}
 Zielerreichung bei Nichtausweis
2
 y 2
EK
[1
]  
2  2 6
 2 2


  
 2 6


 Zielerreichung bei Ausweis von y
2
2
 y

 y
y
EK
[1
] 
    EK
2 2 6


 3
 y

y
  
2 6
 Bei y = 2 beide Werte gleich groß, bei allen y < 2 Wert bei
Nichtausweis strikt kleiner
 Existenz dieses Gleichgewichts bei geringem
Eigenkapitalbedarf, nämlich EK < 0,089
7.41
Bestehende Konkurrenzgefahr und
Kapitalbedarf – Beispiel (2)

2. Vollständiger Ausweis mit N = {1}
 Gleichgewicht bei
2
2
 y 1
 y
EK
[1
]       EK
2  2 6
3
1 1


  
 2 6


 Existenz dieses Gleichgewichts bei hohem Eigenkapitalbedarf,
nämlich EK > 0,048
 Existenz beider Ausweisgleichgewichte für „mittlere“ Werte
von EK

3. Vollständiger Nichtausweis, N = [1, 2]
 Gleichgewicht bei hohem Eigenkapitalbedarf (EK > 0,069)
2
2
 y 1,5 
 y 1 2
 y
EK
EK
[1 
]    [1
]       EK
2  2
6
13  2 4   3 



E   y 1,5  
48
2
6
 



7.42
Bestehende Konkurrenzgefahr und
Kapitalbedarf – Beispiel (3)
4. Teilweiser Ausweis mit N = [1;1,0335]  [1,7024;2]
 Dafür beträgt E[yN] = 1,7667
 Nur wenige Konstellationen, nämlich EK rund um 0,08
0,2
Ausweis
Nichtausweis
0
-0,2
-0,4
-0,6
-0,8
-1
1
1,2
1,4
1,6
1,8
Information
Nichtausweis
0,4
Vorteil bei Ausweis

7.43
2