Multikollinearität - Universität Freiburg
Werbung

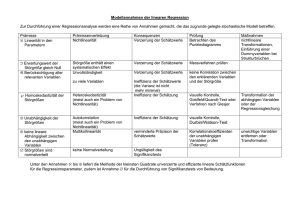
7. Sitzung Multikollinearität Wann spricht man von Multikollinearität? Wenn zwei oder mehrere erklärende Variablen in einem linearen Zusammenhang zueinander stehen. Dabei ist die zugrundeliegende Frage nicht, ob Multikollinearität besteht oder nicht, sondern wie stark diese ausgeprägt ist. Da sich Multikollinearität auf die nicht stochastischen exogenen Variablen bezieht, ist sie eine Eigenschaft der Stichprobe und nicht der Grundgesamtheit. Einige Faustregeln zur Erkennung von Multikollinearität: 1. Hohes R2, bei gleichzeitig insignifikanten t-Werten 2. Bei zwei erklärenden Variablen: der Korrelationskoeffizient ist hoch, d.h. > 0.8 3. Bei mehr als zwei erklärenden Variablen: Überprüfung der partiellen Korrelationskoeffizienten 4. Um in einer Mehrfachregression zu prüfen, welche Variablen sich wie beeinflussen, kann eine Hilfsregression durchgeführt werden 1 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Beispiel : Hohe Korrelation zwischen erklärenden Variablen x1 und x2 kann ein Indiz für Multikollinearität sein Sichtbar an: r1,2 1 (Korrelationskoeffizient misst die lineare Abhängigkeit zwischen zwei exogenen Variablen; hier = 0,977, d.h. hoch) 2 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Eigenschaften: Perfekte Multikollinearität liegt fast nie vor Wird Multikollinearität „diagnostiziert“, handelt es sich dabei meistens um sog. imperfekte Multikollinearität, d.h. den erklärenden Daten – exogenen Variablen – mangelt es an Informationsgehalt Multikollinearität bedeutet nicht zwingend schlechte Datenqualität, wenn z.B. die Störgröße einen geringen Einfluss hat 3 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Je höher die Multikollinearität, umso höher die Varianz der Schätzer Bei Regression mit zwei erklärenden Variablen lautet Varianz von b1: 2 Var (b1 ) 2 2 s11 (1 r12 ) Hohe Multikollinearität kann durch große Variation s211 oder durch geringe Störgrößenvarianz 2 kompensiert werden: 4 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Allgemein gilt: Genauigkeit eines Schätzers ist um so größer (Varianz und Standardfehler umso kleiner), je größer die Varianz der erklärenden Variablen ist. 5 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Multikollinearität kann nicht nur in einer Zweifach-, sondern auch in einer Mehrfachregression vorliegen: y = +... + ß1 ·x1 + ß2 ·x2 + ß3 ·x2 2 + ß4 ·x4 + u, x1 = Schuljahre, x2 = Berufserfahrung, x3 = x2 2 , x4 = Alter Wenn der Korrelationskoeffizient in einer Regression mit zwei exogenen Variablen ein Indikator für Multikollinearität war, ist es nun das Bestimmtheitsmaß R24_123...n einer sog. Hilfsregression in Falle von Mehrfachregressionen, wobei n für die mögliche Anzahl der exogenen Variablen steht: x4 = +... + ß1 ·x1 + ß2 ·x2 + ß3 ·x2 2 + u, x4 = Alter Interpretation: R24_123...n misst die Erklärungskraft der Variablen x1 , x2 usw. für die Werte der Variable x4 , wobei hohes R24_123..n hohe Multikollinearität signalisiert Analoge Berechnung der Bestimmtheitsmaße für alle exogenen Variablen der Mehrfachregression 6 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Beispiel : r4_12...n = 0.999787 7 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Praktische Konsequenzen der Multikollinearität: Trotz der BLUE-Eigenschaft, besitzen die OLS-Schätzer große Varianzen sowie Kovarianzen, was ihre Schätzgenauigkeit beeinträchtigt Die hohen Varianzen bzw. Kovarianzen führen zu breiten Konfidenzintervallen, und somit zu - einer höheren Akzeptanz der Nullhypothese: Ho=0 , d.h. Irrtumswahrscheinlichkeit für den Fehler 2. Art – falsche Hypothese wird nicht verworfen – steigt - insignifikanten t-Werte, trotz hohen Bestimmtheitsmaßes R2 8 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Darstellung von Varianzen und Kovarianzen einzelner Variablen einer Zweifachregression: G L C A B Keine Überschneidung zwischen den Variationen der zwei exogenen Variablen: Variablen unabhängig, KEINE Multikollinearität Überschneidungen mit der endogenen Variable (A und B) dienen zu Parameterschätzung 9 E D F H J I K Überschneidungen E und F: geringe Multikollinearität Lediglich C und D liefern Informationen für die Parameterschätzung Informationen in E sind den exogenen Variablen nicht individuell zurechenbar: gemeinsamer Einfluss G ist Variation der endogenen Variable, die nicht durch die exogenen Variablen erklärt werden kann: Einfluss der Störgrößen Überschneidungen J und K zwischen den Variationen der exogenen Variablen J > E , aber L < G: d.h. stärkere Multikollinearität, ABER höhere Erklärungsgüte H und I liefern Informationen für die Parameterschätzung Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Veranschaulichung der Folgen anhand der Variablen Berufserfahrung und Alter y = +... + ß1 ·x1 + ß2 ·x2 + ß3 ·x2 2 + ß4 ·x4 + u, x1 = Schuljahre, x2 = Berufserfahrung, x3 = x2 2 , x4 = Alter Schwierigkeiten, getrennte Effekte beider Variablen nachzuweisen ungenaue Schätzer, d.h. sehr hohe Varianz niedrige t-Werte, insignifikante Koeffizienten 10 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität 11 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität Interpretation des Outputs, bei dem zwei erklärende Variablen – Alter und Berufserfahrung - hoch korreliert sind: Die Koeffizienten für die korrelierten Variablen sind nicht signifikant von Null verschieden, da die Werte der t-Statistik I t I < 2 sind: I tAlter I = 1,06 und I tBerufserf I = 1,38 Auch haben die Variablen Alter und Berufserfahrung vergleichsweise hohe Standardfehler Die -Fehlerwahrscheinlichkeit ist mit Prob.Alter=29% und Prob.Berufserf=17% hoch Insignifikant Lösungen? 12 Alexander Spermann Universität Freiburg 7. Sitzung Multikollinearität 1. Lösungsansatz: Erhöhung der Anzahl der Observationen - Zeitreihen: z.B. Quartalsdaten statt Jahresdaten - Querschnitt: z.B. OECD statt G7 - Paneldaten 2. Lösungsansatz: Erhöhung der Varianz der exogenen Variablen 3. Lösungsansatz: Indexbildung für ähnliche exogene Variablen 4. Lösungsansatz: Entfernen einer der korrelierten Variablen, kann allerdings auch zu Verzerrung der Schätzung führen, falls die exogene Variable trotz Korrelation einen großen Erklärungsgehalt hat 13 Alexander Spermann Universität Freiburg