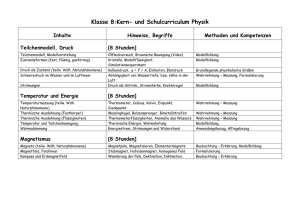
Projekt: Kooperation & Bestrafung:

Projekt: Kooperation &
Egoismus:
Ein Schwarzfahrermodell der S-Bahn
München GmbH
I. Einleitung & Modellbildung
II. Berechnung
a) Input
b) Ausgabe I: Lineare Optimierung
c) Ausgabe II: Nash
d) Ausgabe III: vollständige Kooperation
e) Ausgabe IV: neues Bestrafungssystem
III.Abschluss: Schwarzfahren – Ja oder Nein?
I. Einleitung & Modellbildung
Unterschiedliche Alltagssituationen mit individuellen Entscheidungsmöglichkeiten:
-nicht teilnehmen
-teilnehmen und kooperieren
-teilnehmen aber nicht kooperieren
Unterschiedliche Entscheidungswahl führt zu unterschiedlichem
Nutzen bzgl der Gemeinschaft und einem selbst
(Altruismus (hier: Kooperation; zahlen) vs. Egoismus (hier: Defektor; schwarz fahren))
I. Einleitung & Modellbildung
Das Schwarzfahrermodell:
Das Interesse jedes Einzelnen kollidiert mit dem Interesse der Gruppe:
Einzelner Mitspieler: will nichts bezahlen
Gruppe: will Beförderungssystem aufrecht erhalten
Problematik: Verweigern zu viele Personen die Bezahlung, so bricht das System
zusammen
I. Einleitung & Modellbildung
Begriffe:
Spieltheorie
Schwarzfahrermodell
Kooperatoren
Zahlende Fahrgäste
Defektoren
Schwarzfahrer
Bestrafer
Kontrolleure
Verursachen zusätzliche Kosten; getragen von der Kooperation
=> altruistische Strafe
I. Einleitung & Modellbildung
Modellbildung: Problematik: abstrakt genug für die Mathematik aber exakt
genug zwecks sinnvolle Rückschlüsse für die Realität
I.
Struktur S-Bahn-Netz:
•
Lokale Unterteilung in Stamm, Zone 1, Zone 2, Zone 3
(Stamm = Donnersberger – Ostbahnhof
Zone 3 = Zone 3 + Zone 4)
•
Temporäre Unterteilung in t=1,2,3
(t=1: 05.00 - 10.00 Uhr
t=2: 10.00 – 16.00 Uhr
t=3: 16.00 – 21.00 Uhr)
I. Einleitung & Modellbildung
II.
Fahrgastanzahl G
•
•
Kummulierte Zahl aller Zonen; umgelegt auf nur eine Linie
75% Monatskartenbesitzer
III. Kontrolleure k
• Arbeitszeit: 8 Std. pro Tag
• 2 Kontrolleure bilden 1 Team
• Im Schnitt durchgehend gleiche Anzahl an Teams pro Zone
IV. Schwarzfahrerquote a
• Antizipationsfunktion a = f(k): abhängig von k (=> „Lerneffekt“) und
konstantem Wert d (=> unbeabsichtigtes
schwarzfahren, |d| <<1)
Kein perfekter mathematischer Zusammenhang möglich!
I. Einleitung & Modellbildung
II. Berechnung
a) Input
b) Ausgabe I: Lineare Optimierung
c) Ausgabe II: Nash
d) Ausgabe III: vollständige Kooperation
e) Ausgabe IV: neues Bestrafungssystem
III.Abschluss: Schwarzfahren – Ja oder Nein?
II. a) Input
Beispiel: t=1, Zone=2
Fahrgäste
Prüfquote g12
Schwarzfahrerquote
Schwarzfahrer
(
 teilt als Faktor die Gesamtfahrgäste auf die
unterschiedlichen Zeiten/Zonen auf
)
II. a) Input
Fahrt
von
S
1
2
3
nach
rij=
S
1
2
1
40%
15%
5%
0
60%
35%
10%
0
0
50%
35%
3
0
0
0
50%
II. a) Input
Beispiel: t=1, Zone=2
Gesamtumsatz U = Fahrpreiseinnahmen E – Personalkosten P + Einnahme Bußgelder
+
-
II. a) Input
Fahrgäste:
750.000
Kontrolleure: 5
4
3
1
f(x)= 0,27/sqrt(x)
I. Einleitung & Modellbildung
II. Berechnung
a) Input
b) Ausgabe I: Lineare Optimierung
c) Ausgabe II: Nash
d) Ausgabe III: vollständige Kooperation
e) Ausgabe IV: neues Bestrafungssystem
III.Abschluss: Schwarzfahren – Ja oder Nein?
IV.Anwendung Excel
II. b) Ausgabe I: Lineare Optimierung
Anzahl x
x1
x2
Verteilung v
v1 = (v1S, v11, v12 v13)
(erwischte Schwarzfahrer;
...
Personalkosten)
v2 = (v2S, v21, v22 v23)
...
...
vn = (vnS, vn1, vn2 vn3)
Problem: Nash-Gleichgewicht? n konvergiert gegen unendlich!
... xn
II. b) Ausgabe I: Lineare Optimierung
Beispiel: t=1, Zone=2
exemplarische Rechnung für eine Bimatrix:
Anzahl k
x1=13
x2=26
v1 = (0,385 ; 0,308 ; 0,23 ; 0,07)
(91; -2600)
(162; -5200)
v2 = (0,62 ; 0,31 ; 0,07 ; 0)
(150; -2600)
(270; -5200)
Verteilung v
 v2 dominiert v1, da bei gleichen Personalkosten immer mehr Schwarzfahrer
erwischt werden; untersuche also nur v2 auf bestmöglichen Umsatz
 Gesamtumsatz ergibt: U(v2, x1) = 303.000
U(v2, x2) = 305.000
I. Einleitung & Modellbildung
II. Berechnung
a) Input
b) Ausgabe I: Lineare Optimierung
c) Ausgabe II: Nash
d) Ausgabe III: vollständige Kooperation
e) Ausgabe IV: neues Bestrafungssystem
III.Abschluss: Schwarzfahren – Ja oder Nein?
II. c) Ausgabe II: Nash
Reale Schwarzfahrerquote nicht identisch mit dem
Nash-Gleichgewicht!
Gründe:
-wahre Größen nicht bekannt
-ethisch (Moral-Betrug)
-Peinlichkeitsfaktor
-etc
II. c) Ausgabe II: Nash
Beispiel: t=1, Zone 2
kontrollieren
zahlen
(-4,40 ; -C2 +4,40
nicht zahlen
(-40
nicht kontrollieren
) ( -4,40 ; +4,40 )
; -C2 + (20-4,40) ) ( 0
; -4,40 )
I. Einleitung & Modellbildung
II. Berechnung
a) Input
b) Ausgabe I: Lineare Optimierung
c) Ausgabe II: Nash
d) Ausgabe III: vollständige Kooperation
e) Ausgabe IV: neues Bestrafungssystem
III.Abschluss: Schwarzfahren – Ja oder Nein?
II. d) Ausgabe III: vollständige Kooperation
Nur Kooperatoren, keine Defektoren
=> jeder Fahrgast zahlt
=> Kontrolleure unnötig
=> Gewinn steigt
=> wird eingesetzt um Fahrpreis zu senken
=> erwartete Zahlung der Gemeinschaft wird geringer
II. d) Ausgabe III: vollständige Kooperation
Beispiel: t=1, Zone=2
Liegt nun der neue Umsatz höher als der alte, so lässt sich
der Fahrpreis bei gleichbleibendem Gewinn senken um den
Faktor u/u‘.
u entspricht dabei dem ursprünglichen Gewinn, der gleich bleiben soll!
II. d) Ausgabe III: vollständige Kooperation
Problematik: Umsetzung in die Realität (Homo Oeconomicus)
„Teufelskreis“ beginnt wieder:
mehr
Defektoren
steigender
Fahrpreis
weniger
zusätzlicher
Gewinn
Resultat: In der Praxis ist das Bestrafungssystem unerlässlich!
I. Einleitung & Modellbildung
II. Berechnung
a) Input
b) Ausgabe I: Lineare Optimierung
c) Ausgabe II: Nash
d) Ausgabe III: vollständige Kooperation
e) Ausgabe IV: neues Bestrafungssystem
III.Abschluss: Schwarzfahren – Ja oder Nein?
II. e) Ausgabe IV: neues Bestrafungssystem
bisher: 40 € Bußgeld
bei sofortiger Zahlung keine unbedingte Speicherung der Personendaten
=> Fahrgast steht jedes mal wieder vor der selben Entscheidung ob zahlen
oder schwarz fahren; Keine Veränderung der Nash-Werte!
(folglich ist eine Iteration dieses Spiels unnütz)
neu: gestaffeltes Bußgeld-System (bsp.: Österreich)
hier: (q+1)*40 € Bußgeld fällig, für q = Anzahl wie oft man zuvor schon
erwischt wurde
Speicherung der Personendaten bei jedem Fall
=> Fahrgast steht in Abhängigkeit von q jedesmal wieder vor einem
neuen „Spiel“ mit anderen Nash-Gleichgewichten!
II. e) Ausgabe IV: neues Bestrafungssystem
Beispiel: t=1, Zone=2
q=2
kontrollieren
zahlen
(-4,40 ; -C2 +4,40
nicht zahlen
(-120 ; -C2 + (60-4,40) ) ( 0
 g12 = 4,40 / 120
= 4%
 a12 = -C2 / (0,5 * 120) = 11%
nicht kontrollieren
) ( -4,40 ; +4,40 )
; -4,40 )
I. Einleitung & Modellbildung
II. Berechnung
a) Input
b) Ausgabe I: Lineare Optimierung
c) Ausgabe II: Nash
d) Ausgabe III: vollständige Kooperation
e) Ausgabe IV: neues Bestrafungssystem
III.Abschluss: Schwarzfahren – Ja oder Nein?
III. Abschluss: Schwarzfahren – Ja oder Nein?
Zum Abschluss noch die Antwort auf die Frage,
die wahrscheinlich für den studentischen Zuhörer als
wirtschaftlichen und mathematischen Spieler
am interessantesten ist:
Was kostet Schwarzfahren in München und
wann sollte man in jedem Fall ein Ticket kaufen?
- vielleicht eher eine Frage der Wahrscheinlichkeitsrechnung als der
Spieltheorie, aber in Zusammenhang zu diesem Projekt wird
sich der ein oder andere (ohne Moral handelnde) sicher genau
diese Frage das nächste Mal stellen :)
Danke für ihre Aufmerksamkeit