T 1 - TUM

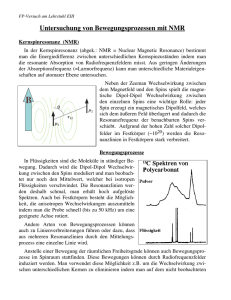
Magnetische Kernresonanz
(NMR)
Erstellt von Andreas Fuhrmanek
23.11.2004
Inhalt
1.
2.
2.1
2.2
2.3
3.
3.1
3.2
3.3
4.
4.1
4.2
5.
6.
Einleitung
Theorie der NMR
Hyperfeinstruktur
Kernmagnetisierung
Bloch-Gleichungen
Experimentelle Umsetzung
CW-Methode
Gepulste Resonanz
Problembehandlung
Anwendungsbeispiele
Strukturaufklärung in der Chemie
MRT
Ausblick
Literaturnachweise
1. Einleitung
• Entdeckt 1945 von Edward Purcell und
von Felix Bloch
• Analogie zur Elektronenresonanz
• Kernspinresonanz, Kerninduktion,
magnetische Kernresonanz sind andere
Bezeichnungen
• In der Medizin: MR-Tomograph
• Keine Zerstörung der
untersuchten Materie
(E<0,3Jmol-1)
• Von -190 bis +300°C
anwendbar
• Nachteil: Kerne mit I=0 zeigen
keine Resonanz → Isotope
verwenden
• Aufklärung der
Bindungsstruktur zwischen
Kernen
• Spektren sind oft nicht
eindeutig
2.0 Theorie der NMR
2.1 Hyperfeinstruktur
 Eigendrehimpuls des Kerns erzeugt magnetisches
Kernmoment
 Vorgehensweise analog zum Elektronenspin
Die positive Ladung +Ze des Kerns erzeugt ein
magnetisches Moment:
I
µi  g i µK

Für die z-Komponente des
Kernmoments gilt dann:
µi , z  g i µK mi
 gi ist der Kern g-Faktor
 µK ist das Kernmagneton, welches analog zum
Bohrschen Magneton definiert wird:
me
e
 27 J
µK 
 µB
 5,05078317 10
2m p
mp
T
 Das Massenverhältnis aus Kern und Elektron beläuft
sich auf
mP
 1836
me
 Protonen g-Faktor:
g P  5,585
(a) Elektronbahnbewegung erzeugt B-Feld am Kernort
(b) µs erzeugt BHFS am Kernort und wechselwirkt mit µI
(c) Kopplung von J und I zu F=J+I
Die Zusatzenergie durch das Kernmoment ist:
Mit folgenden Beziehungen lässt sich diese Energie
berechnen:
Der Cosinusterm kann dann berechnet werden.
Für EHFS erhält man so:
mit
Für das Wasserstoffatom z.B. erhält man im Grundzustand:
2.2 Kernmagnetisierung
Boltzmannverteilung der M Unterzustände im thermischen Gleichgewicht:
 Emagn M 
P( M )  exp 

k
T
B


Daraus ergibt sich eine Polarisation. Bei nicht zu tiefen Temperaturen gilt:
 Emagn ( M ) 

M

exp

 k T 
 2 I ( I  1)
M  I
B




B0
I
3k BT
 Emagn ( M ) 
exp 


k
T
M  I
B


I
Iz
Für die Magnetisierung folgt dann:
M z  N I z  N
 2 I ( I  1)
3k BT
B0
2.3 Bloch-Gleichungen
Äußeres B-Feld → Änderung der
Magnetisierung

 
dM
  ( M  B)
dt
Magnetisierungsvektor präzidiert
um B mit der Lamorfrequenz
L  B
Grundprinzip: Anregende Photonen:
E  hL
1. Rotierendes
Koordinatensystem
2. Transformation →
Term, wie bei
Corioliskraft
3. Langsame Änderung
des HF-Magnetfeld
→ dM/dt~0
L  B0
Gyromagnetisches Verhältnis:
 
N

Drehendes Koordinatensystem:
Abweichung von der Magnetisierung:
dM z M 0  M z

dt
T1
T1: Spin-Gitter Relaxationszeit
Zeit, die eine unmagnetisierte
Probe braucht, um vollständig
magnetisiert zu werden
Erklärung von T2:
dM x
M
 x
dt
T2
dM y
dt

My
T2
T2: Spin-Spin Relaxationszeit
Zeit, die vergeht, wenn zwei
in Phase gerichtete
Kernmomente außer Phase
geraten
Hochfrequentes Magnetfeld BHF wird in x-yEbene angelegt
 
M0  M z
dM z
  (M  B) z 
dt
T1
 
dM x
Mx
  (M  B) x 
dt
T2
 
dM y
My
  ( M  B) y 
dt
T2
wobei:
  
B  B0  BHF
Im thermischen Gleichgewicht erhält man
für die Magnetisierung:
3. Experimentelle Umsetzung
3.1 Continuous Wave-Methode
• kleines HF-Feld (B~10-7T)
• Anregung mit Radiofrequenz (H: 60-800MHz)
• detektiere Emission der absorbierten Strahlung
• Magnetisierung erzeugt induzierte Spannung in der
Sendespule (Purcell-Methode)
U Ind
~
~
 A0 ( M x sin t  M y cos t )
Eine Empfängerspule kann Mx und My messen.
Mx: Dispersionskurve
My: Absorptionskurve
Absorptions-, Dispersionsspektrum
S: Größe prop. zur Stärke von BHF
F: prop. zum Magnetfeld B0
Durch Bestimmung der Linienbreite erhält man
Information über T1 und T2:
A)
Schwaches
Wechselfeld
2
 
T2
T2 : transversale,
Spin-SpinRelaxationszeit
B) Starkes Wechselfeld
  2BHF
T1
T2
T1 : longitudinale, Spin-
Gitter-Ralaxationszeit
Signalverstärkung
a) Purcell-Brücke ~
Brückenschaltung
b) Lock-In Verstärker:
Bandfilter mit
schmaler
Frequenzbreite
Aufbau einer
Brückenschaltung
3.2 Gepulste Kernresonanz
• Kurzer Magnetfeldpuls (~10-3T)
• Abschalten des HFFeldes →
Relaxationsprozess
• Kerne sehen
unterschiedliche B0Felder
• Alle
Präzessionsfrequenzen
werden beobachtet
• Empfängerspule nimmt
Spannungen auf
• Puls von 10µs →
Frequenzbereich von
100000 Hz
Impuls-FT-NMR-Spektroskopie
• Spannungen verhalten sich wie Fourier-Spektrum
• Trafo ergibt alle Resonanzfrequenzen
• Gepulste Kernresonanz = Impuls-FT-NMR
Vergleich von CW und FT
Spin-Echo
• Inhomogenität der externen Felder
• Dipol-Dipol WW
→ Auseinanderlaufen der Spins
• Erwin Hahn, 1950
• nach Relaxation T1, p-Puls → Echo
• Ausmittelung von WW, die
Linienverbreiterung verursachen
3.3 Problembehandlung
• In Lösung, Ausmittelung anisotroper
Effekte, Linienbreite < 0,1Hz
• Im Festkörper:
a) Zeemann-WW von I mit B0,BHF
b) Dipol-Dipol Kopplung der Kernspins I
c) magn. Abschirmung von I durch Elektr.
(chemische Verschiebung)
• Festkörper: Linienbreite bis zu einigen kHz
Lösung 1: MAS (Magic Angle Spinning)
entwickelt von Lowe, Andrews, 1959
• Hamiltonoperator der Dipol-Dipol-WW:
2
h
ˆ
H D   3  i j ((3 cos 2  )  1)( I i I j  3I iz I jz )
i  j 2r ij
Nachteile:
a) Dipol-WW darf nicht zu groß sein
b) Quadrupol-WW kann nur teilweise eliminiert
werden
c) Einschränkung durch Rotationsfrequenz
Chemische Verschiebung

µz

B0 
B0
2p
Ih
→ gleiches I, gleiches
Spektrum? Nein!
Hˆ 0  H 0  Hˆ 0 (t )
• Hamiltonoperator kann separiert werden
• zeitlicher Mittelwert + zeitabhängiger Teil
• Schnelle Rotation → Ausmitteln von H(t)
• Schnelle Rot. (4 kHz)
→ Info zur Isotropen
chem. Verschiebung
• Langsame Rot. →
Seitenbänder →
anisotrope Versch.
• Schnelle Rotation
durch Gasantrieb
• Material und Frequenz
bestimmen natürliche
Schranke
Lösung 2: Cross Polarisation (CP)
Vorteile:
• Erhöhung der Empfindlichkeit um Faktor 4
• Verkürzung der Wiederholungsrate T1
H
• Empfindlichkeit von 1H auf X-Kerne, da 
X
Hartmann-Hahn-Beziehung für das
Radiofeld:
 H B1H   X BX
Spin-Locking:
4. Anwendungsbeispiele
4.1 Spektroskopie in der Chemie
Absorptionsfrequenz bei 2,35T
(B-Feld bei gleicher Einstrahlfrequenz (100MHz) )
Problem der Auswertung
Identische Spektren, Feiner Unterschied in der
Höhe des Signals
Spektrum von 2-Buthanol
- oben: 1H Breitband (BB)-gekoppelt - Multipletts
- unten: 1H BB-entkoppelt → Singuletts+Intensitätserhöhung
4.2 MRT–Magnetic Resonance Tomographie

Umsetzung der NMR für medizinische Zwecke
 Lauterbur, Mansfield (1973)
 Nobelpreis für Medizin in 2003
 Körper besteht zum Großteil aus 1H-Atomen
 Kontrastmittel:
Gadoliniumverbindungen
 Keine Schädigung
des Gewebes
 Bestrahlung mit
Radiowellen
MR-Tomograph von Siemens
Hülle:
 Heliumgekühlter supraleitender Elektromagnet
 Sende- und Empfangsantennen
5. Ausblick
• Erforschung von
Festkörpern im
Hinblick auf neue
Materialien
• Ausschalten der
Störungen (chem.
Versch., DipolKopplung)
• Verbesserung des
MAS-Experiments
6. Literaturnachweise
•
Chemie in unserer Zeit, 21. Jahrg. 1988, Nr. 3
•
http://www.chemlin.de/chemie/nmr_spektroskopie.htm
•
The Feynman Lectures on Physics, Band II
•
C.A. Fyfe, Solid State NMR for Chemists