NMR und MRI
Werbung
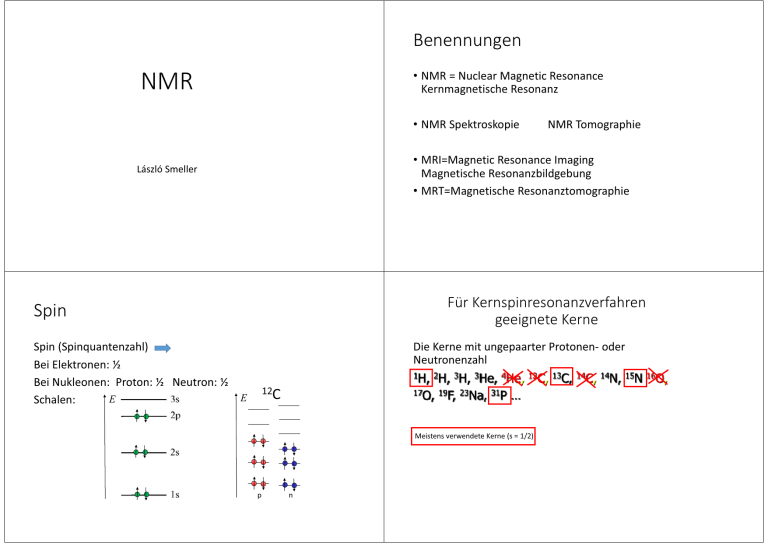
Benennungen • NMR = Nuclear Magnetic Resonance Kernmagnetische Resonanz NMR • NMR Spektroskopie NMR Tomographie • MRI=Magnetic Resonance Imaging Magnetische Resonanzbildgebung • MRT=Magnetische Resonanztomographie László Smeller Für Kernspinresonanzverfahren geeignete Kerne Spin Spin (Spinquantenzahl) Bei Elektronen: ½ Bei Nukleonen: Proton: ½ Neutron: ½ E E Schalen: Die Kerne mit ungepaarter Protonen- oder Neutronenzahl 1H, 2H, 3H, 3He, 4He, 12 2C, 13C, 1 14 4C, 14 4N, 15N 17O, 19 19F, 23 23Na, 31 1P … 12C Meistens verwendete Kerne (s = 1/2) p n 16 6O, Spin, magnetisches Moment Spin Spin, magnetisches Moment Naive Erklärung aus der klassischen Physik: magnetisches Moment () [J/T] Elementarteilchen mit von null unterschiedlichem Spin weisen eigenes magnetisches Moment auf. = ħ s spin I ħ=h/(2) Proton Neutron Planksche Wirkungskonstante giromagnetisches Verhältnis Unterschiedlich für alle Elementarteilchen und Kerne Joule = SI Einheit der Energie Tesla = SI Einheit des Magnetfeldes zB: Proton=2,67·108 T-1s-1 Zeemansche Aufspaltung Zeemansche Aufspaltung Teilchen mit einem Spin von ± ½ • Energiezustand: • a.) ohne Magnetfeld — unabhängig vom Spinzustand • b.) mit Magnetfeld: Aufspaltung des Energieniveaus — Zeemansche-Aufspaltung Teilchen mit einem Spin von ± ½ (zB: Proton = H Atomkern …) a b B • Energiezustände in einem Magnetfeld E B0 B antiparallel E=B0 B0 parallel instabiler Zustand stabiler Zustand höhere Energie niedrigere Energie Magnetische Feldstärke B0 Zeemansche Aufspaltung Teilchen mit einem Spin von ± ½ E=B0=ħB0 Photonen mit Ephoton=hf=E können Spinübergänge verursachen. = 2 Boltzmannsche Verteilung s=1 E E na/np=e-E/kT antiparallel photon 1, 2, … 1, 2, … Bei B0=1T für ein Proton: E=2,8·10-26 J (=1,75 ·10-7eV) f=E/h=2,8·10-26 J / 6,63·10-34 Js = 4,26 ·107 Hz = 42,6 MHz Bei B = 0,6 T E 10-7 eV na np nanp zB.: wenn na+np=2 000 000 dann na-np=4 parallel Radiowelle! Klassische Beschreibung: Präzession Präzession wegen des Drehmomentes B0 d.h.: 4 aus 2 000 000 Kerne sind nicht ausgeglichen Konventionelle Messung der Kernresonanz Frequenz der Präzession: Larmor Frequenz = 2 Resonanz mit dem äußeren Wechselmagnetfeld der zum Spinübergang angewandten Radiowelle kT 0,025 eV (bei Körpertemp.) S Wechselstrom mit einer Frequenz von f. f wird variiert. B0 Resonanzsignal Probe N fL f Moderne FT* Methode zur Messung der Resonanzfrequenzen Moderne FT Methode zur Messung der Resonanzfrequenzen Eine Probe hat viele (1023) Kerne die alle mit einer Larmor –Frequenz präzedieren. Betrachten wir 2 000 000 Kerne: B0 B0 B0 B0 np=1000000+2 z = 2 Nach einer Bestrahlung aus Richtung x mit Radiowellen, deren Frequenz gleich mit fL ist: np=1000000+1 M = y x Resultierende Magnetisierung in der z Richtung na=1000000-2 Moderne FT Methode zur Messung der Resonanzfrequenzen na<~ np z Was verursacht also der 90° Impuls y zusammenfassend? B0 90° B0 Resultierende Magnetisierung in der z Richtung 90° Radiowelle 90° Imp. na=1000000 Resultierende Magnetisierung dreht sich in die Richtung der x-y Ebene na=1000000-1 np=1000000 = 2 y x Radiowelle x Nach einer Bestrahlung aus Richtung x mit einem 90° Impuls: B0 2 na< np * FT= Fourier Transformation synchronisierte Präzession z Resultierende Magnetisierung in der x-y Ebene na = np na <~ np E … … vor der Bestrahlung Resultierende Magnetisierung in der x-y Ebene Radiowelle 90° Imp. na = np E … … nach der Bestrahlung z Moderne FT Methode zur Messung der Resonanzfrequenzen y Moderne FT Methode zur Messung der Resonanzfrequenzen Der 180° Impuls x Freier Induktionsabfall (Free Induction Decay: FID) nach einem 90° Impuls B0 180° B0 Uind Resultierende Magnetisierung in z Richtung Radiowelle 180° Imp. na < np E E … Resultierende Magnetisierung in -z Richtung z na > np x y … … Resultierende Magnetisierung in y Richtung na = np … vor der Bestrahlung 90° t Uind Induzierte Spannung T= Periodenzeit f=1/T nach der Bestrahlung Spektrum aus dem FID Signal NMR Spektroskopie Uind Resonanzsignal t FT fL Fourier Transformation f Wirksames Magnetfeld (Beff) an einem Proton (H Atomkern) in einem Molekül ist unterschiedlich von B0 wegen • chemischer Abschirmung verursacht von der Elektronen (BCS) • Wechselwirkung zwischen Protonen (BSC) • … Beff = B0+BCS +BSC +…=B0(1-) Chemische Verschiebung: Lokales Magnetfeld Chemische Verschiebung Ein Elektron im Magnetfeld bewegend verursacht ein eigenes Magnetfeld was gegen dem äußeren Magnetfeld wirkt (Abschirmung) Die Abschirmung häng von der Elektronenstruktur ab. Chemische Verschiebung gibt Information über der Molekülstruktur. B0 R e̶ BCS F v F=B0ev F=mv2/R R= Abschirmung vermindertes lokales Magnetfel Larmor Frequenz nimmt ab. Grössere Elektronendichte Erhöchte Abschirmung I = I= 2 = Referenzstoff: Tetramethylsilan BCS = − C4H12Si ~ Spin-Spin Kopplung (J-Kopplung) Das NMR-Spetrum Wirkt durch kovalente Bindungen Signal Intensität Ha Hb | | R C C R’’’ | | R’ R’’ Signal Intensität 60,0006 MHz 60,00000 MHz bei B0 = 1,409248 T 1, 409234 T 1,409248 T 600 Hz Chemische Verschiebung in ppm: δ = 0 Hz Bei f = 60 MHz chem. Verschiebung (!"#$%#%) (!"#$%#%) 106 B0 Feld der chemishen Verschiebung Feld des Hb-Atoms in der zwei Spinzustandes -1/2 +1/2 Signal Intensität Chemsiche Verschiebung Signal des für das Duplet a H Atoms wenn Feld des Hb Atoms ist ↓ Signal des Ha Atoms wenn Feld des Hb Atoms ist ↑ Spin-spin Kopplung Mehrdimensionale NMR Spektroskopische Methoden Beispiel: NMR Spektrum des Ethanols: Allgemeine Informationen: Intensität ist mit Hilfe der Niveaulinien dargestellt. Diagonale Spitzen: Entsprechen zur 1D spektrum bei homonuklearen Spektrum Mehrdimensionale NMR Spektroskopische Methoden Beispiele Lysozyme HQSC Spektrum COSY (engl. correlation spectroscopy) -Homonuklear -Heteronuklear Misst die skalare Kopplung (miteinander verbundene Atome) NOESY (engl. nuclear overhauser enhancement and exchange spectroscopy) Das Signal zeigt räumlich benachbarte Kerne wenn sie nicht skalar miteinander koppeln (d.h. nicht mit chemische Bindung gebunden sind). HSQC (engl. heteronuclear single quantum coherence) Das Signal zeigt die direkt aneinander gebundene Atome … Quelle: Wikipedia Quelle: K. Akasaka et al. / Archives of Biochemistry and Biophysics 531 (2013) 110–115











