Schwingungsspektroskopie

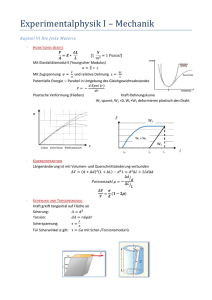
Schwingungsspektroskopie
Vortrag im Rahmen des PC-Seminars für Biochemiker
30.01.2004
Frederik Uibel
Andreas Maurer
Molekülbewegungen
Translation:
Die Bewegung des gesamten Moleküls in die
drei Raumrichtungen.
Rotation:
Drehung des gesamten Moleküls um die drei
Drehachsen.
Schwingung: Periodische Bewegung einzelner Atome
oder Atomgruppen eines Moleküls relativ
zueinander.
Molekülschwingungen
Moleküle schwingen, da die Atome nicht starr
sondern elastisch, vergleichbar mit Federn in der Mechanik,
miteinander verbunden sind.
Wie in der Mechanik gilt auch hier das Hookesche Gesetz:
F = -k*x
Freiheitsgrade
Die einzelnen Atome eines Moleküls können sich in drei
Raumrichtungen bewegen. Die kombinierte Bewegung aller
Atome führt zu Translation, Rotation oder Schwingung des
Moleküls.
Ein Molekül mit N Atomen hat 3N Freiheitsgrade.
Ein zweiatomiges Molekül besitzt z.B. folgende
Freiheitsgrade:
3 mal Translation
In alle drei Raumrichtungen
2 mal Rotation
Um die beiden
Querachsen
1 mal Schwingung
?
Freiheitsgrade
Allgemein gilt für Schwingungsfreiheitsgrade, wenn N die
Anzahl der Atome eines Moleküls ist:
Für lineare Moleküle:
Zahl der Schwingungsfreiheitsgrade = 3N-5
Für nichtlineare Moleküle:
Zahl der Schwingungsfreiheitsgrade = 3N-6
Arten von Molekülschwingungen
Am Beispiel des CO2 (Freiheitsgrade der Schwingung: 4)
Symmetrische Valenzschwingung
Asymmetrische Valenzschwingung
Deformationsschwingungen
Das Modell des harmonischen
Oszillators
Schema der potentiellen
Energie in Abhängigkeit
von der Auslenkung bei
einer harmonischen
Schwingung:
Parabel wird beschrieben
durch:
1 2
V  kx
2
Die Realität: Der anharmonische
Oszillator
Dissoziation des Moleküls
bei zu hoher Energie
Überproportionale Zunahme
der potentiellen Energie bei
Annäherung der Atome
Die Realität: Der anharmonische
Oszillator
Die Kurve kann beschrieben
werden durch folgende Gleichung:
V  hcDe 1  e

a x 2
Morse-Potential
x Sog.
 Auslenkung
De  Dissoziationsenergie
a

2hcDe

  reduzierte Masse
  2 0
Energieeigenwerte und
Schwingungsterme
Harmonischer Oszillator:
Energieeigenwerte:
1

E (v)  h 0  v  
2

1
k
v0 = Schwingungsquantenzahl (v = 0,1,2...)
2 
Schwingungsterme:
E (vMasse:
)
1  1  1
Reduzierte
G (v ) 
 0  v  
hc
 m21 m2
Ein Schwingungsterm entspricht einem
Energieeigenwert ausgedrückt in der
Wellenzahl.
Energieeigenwerte und
Schwingungsterme
Man erhält äquidistante
und diskrete
Schwingungsniveaus,
jeweils im Abstand

Energieeigenwerte und
Schwingungsterme
Anharmonischer Oszillator:
2
Schwingungsterme:
1
1


G (v)   v   0   v   xe 0
2
2


Anharmonizitätskonstante:
0
a2
xe 

2 4 De
Energieeigenwerte und
Schwingungsterme
Man
erhält
für
den
anharmonischen
Oszillator
Schwingungsniveaus, die nicht
mehr äquidistant sind, sondern sich
mit zunehmendem v immer mehr
annähern. Es gibt nicht unendlich
viele Energieniveaus.
2
1
1


G (v)   v   0   v   xe 0
2
2


Schwingungsspektroskopie
Moleküle absorbieren elektromagnetische Strahlung im
Infrarotbereich
 Anregung von Schwingungsübergängen
Da die Schwingungsenergie gequantelt ist, werden nur
bestimmte Wellenlängen absorbiert. Man erhält ein
Schwingungsspektrum.
Allgemeine Auswahlregel
Nach den Gesetzen der Physik kann elektromagnetische
Strahlung nur mit einem oszillierenden Dipol
wechselwirken. Ein oszillierender Dipol liegt vor, wenn sich
das Dipolmoment über die Zeit ändert.
Deshalb sind nur Schwingungen, bei denen sich das
Dipolmoment ändert, IR-aktiv.
Das elektrische Dipolmoment berechnet sich nach
p  q l
Allgemeine Auswahlregel
Ein oszillierender Dipol
entsteht, wenn sich bei
der Schwingung die
Ladungsschwerpunkte
relativ
zueinander
bewegen.
p  q l



l
 



l
Allgemeine Auswahlregel

Oszillierender
Dipol!
Dipolmoment

Kein Dipolmoment
 
Dipolmoment


l
l
Allgemeine Auswahlregel
Symmetrische Valenzschwingung
Asymmetrische Valenzschwingung
IR-inaktiv
IR-aktiv
IR-aktiv
IR-aktiv
Deformationsschwingungen
Spezielle Auswahlregeln
Mit Hilfe der zeitabhängigen Schrödingergleichung erhält
man außerdem spezielle Auswahlregeln für die
Schwingungsübergänge. Diese lauten:
Für den Harmonischen Oszillator:
v  1
Das bedeutet, dass nur Schwingungsübergänge zwischen
benachbarten Energieniveaus erlaubt sind.
Spezielle Auswahlregeln
Mit Hilfe der zeitabhängigen Schrödingergleichung erhält
man außerdem spezielle Auswahlregeln für die
Schwingungsübergänge. Diese lauten:
Für den Anharmonischen Oszillator:
v  1, 2,3,...
Hier sind auch Übergänge in entferntere Niveaus, sogenannte
Oberschwingungen, erlaubt, allerdings nimmt die
Wahrscheinlichkeit eines Übergangs mit zunehmender
Entfernung der Niveaus ab.
RotationsSchwingungspektroskopie
Wenn ein Molekül einen Schwingungsübergang durchführt,
ist dies normalerweise auch mit einem Rotationsübergang
verbunden.
Grund: Durch die Anregung eines höheren
Schwingungszustandes verändern sich die Bindungslängen
im Molekül und damit sein Trägheitsmoment, welches
wiederum Einfluss auf die Rotation des Moleküls nimmt.
RotationsSchwingungspektroskopie
Die Rotationsquantenzahl J ändert sich hierbei um 1
Manchmal ist ein Schwingungsübergang auch ohne
Rotationsübergang möglich (ΔJ=0)
Dies hängt dann mit der Struktur des Moleküls zusammen:
Es muss ein Drehimpuls um die Molekülachse stattfinden
können. Dies ist z.B. beim NO oder der
Deformationsschwingung des CO2 der Fall.
RotationsSchwingungspektroskopie
Als Auswahlregeln bei der RotationsSchwingungsspektroskopie erhält man:
v  1
J  1, 0
1

Rotations-Schwingungsterme: S(v, J)   v   0  BJ  J  1
2

RotationsSchwingungspektroskopie
Termschema:
Eine Linie
steht für einen
kombinierten
RotationsSchwingungsübergang!
RotationsSchwingungspektroskopie
Man erhält ein Spektrum der folgenden Art:
RotationsSchwingungspektroskopie
Oder mit Q-Zweig:
Spektren
Scharf hervortretende Linien treten nur bei Spektroskopie in
der Gasphase auf.
In kondensierten Phasen sind die Linien teilweise bis stark
verschwommen.
Grund: Kondensierte Phasen behindern die Rotation des
Moleküls
Spektren
Spektren von Benzol
Im gasförmigen Zustand
im flüssigen Zustand
Praktische Anwendung
•
Das Infrarot-Spektrum einer bestimmten Substanz ist
charakteristisch und kann zu ihrer Identifizierung
dienen
•
Informationen über die Struktur des Stoffes sind im
Spektrum enthalten
•
Fingerprinting: Schwingungen bei bestimmten
Wellenzahlen können bestimmten Molekülgruppen
zugeordnet werden.
Praktische Anwendung
Spektren von CO2
Spektren von CO2
Lust auf mehr???
H. Günzler, H. M. Heise:
IR-Spektroskopie, 3. Aufl., ISBN:3-527-28759-0
Peter W. Atkins:
Physikalische Chemie, 3. Aufl., ISBN 3-527-30236-0
Diese Folienserie im Internet:
http://homepage.uni-tuebingen.de/student/andreas.maurer/