Formelsammlung (2. Teil
Werbung
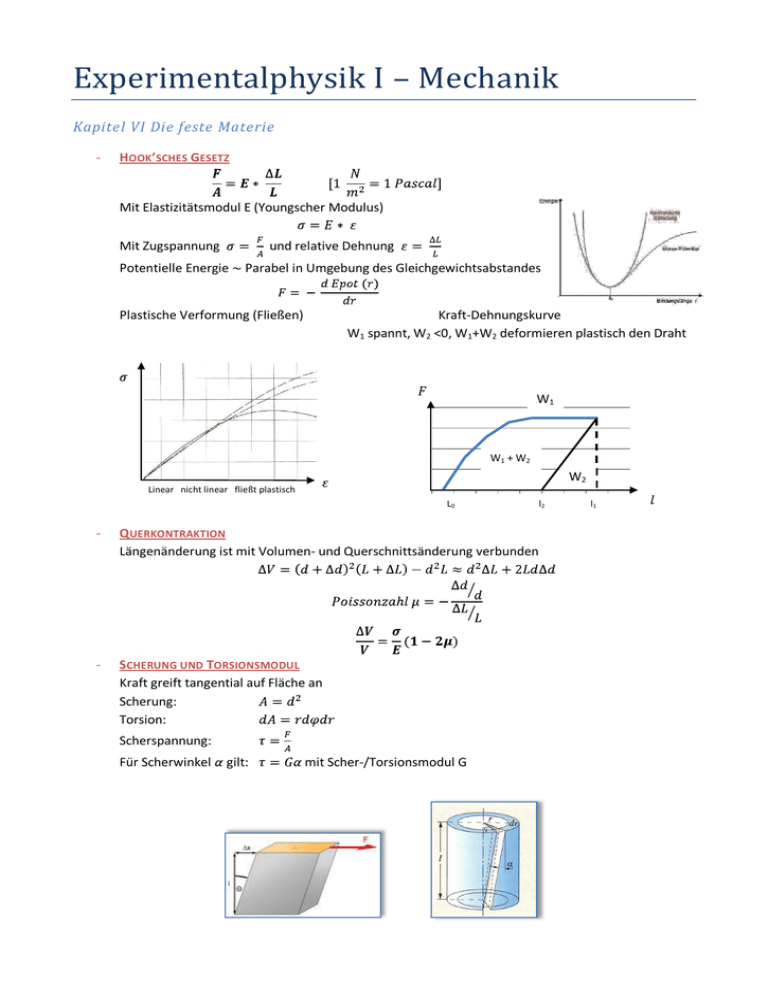
Experimentalphysik I – Mechanik Kapitel VI Die feste Materie - HOOK’SCHES GESETZ Mit Elastizitätsmodul E (Youngscher Modulus) Mit Zugspannung und relative Dehnung Potentielle Energie Parabel in Umgebung des Gleichgewichtsabstandes Plastische Verformung (Fließen) Kraft-Dehnungskurve W1 spannt, W2 <0, W1+W2 deformieren plastisch den Draht W1 W1 + W2 W2 Linear nicht linear fließt plastisch L0 - Q UERKONTRAKTION Längenänderung ist mit Volumen- und Querschnittsänderung verbunden - SCHERUNG UND TORSIONSMODUL Kraft greift tangential auf Fläche an Scherung: Torsion: Scherspannung: Für Scherwinkel gilt: mit Scher-/Torsionsmodul G l2 l1 Kapitel VII Schwingungen - FREIE UNGEDÄMPFTE SCHWINGUNG Bewegungsgleichung: für Federpendel Allgemeine Lösung: Beispiele: o Torsionspendel BG: o Fadenpendel BG: o U-Rohr BG: Physikalisches Pendel (Körper schwingt um Achse mit Abstand d zum Schwerpunkt) Energie im harmonischen Oszillator Komplexe Schreibweise: - FREIE GEDÄMPFTE SCHWINGUNG Reibungskraft ist entgegengesetzt proportional zur Geschwindigkeit Bewegungsgleichung: Lösung: Mit und Exponentielles Abklingen der Amplitude Energie des gedämpften harm. Oszillators für d.h. Gesamtenergie fällt nach der Zeit auf den e-ten Teil Güte des Oszillators mit ist die im Zeitintervall Für schwach gedämpfte Oszillatoren gilt: Wenn abgegebene Energie oder pro Periode gegeben ist: Aperiodischer Grenzfall Hier gibt es weitere Lösungen: und Starke Dämpfung wird imaginär Schwingung geht über in exponentielles Abklingen - A1 und A2 sind Anfangsbedingungen von x(0) und v(0), ERZWUNGENE SCHWINGUNG Periodische äußere Kraft , sind Zeitkonstanten Bewegungsgleichung: Für Federpendel: , , Allgemeine Lösung der homogenen DGL + spezielle Lösung der inhomogenen DGL: 1.Term bezeichnet gedämpfte Schwingung mit 2.Term ist die erzwungene, stationäre Schwingung wird maximal für (beim Einschwingen) ( ) wird maximal für wird maximal bei Halbwertsbreite bei mit damit ist Q ein geeignetes Maß für die Resonanzschärfe (scharf für schwache Dämpfung) - GEKOPPELTE OSZILLATOREN Zwei gekoppelte Bewegungsgleichungen: Führe neue Koordinaten ein: Also kann gekoppeltes Pendel gleichphasig mit (bei und gegephasig (bei mit schwingen. Wenn beide Schwingungstypen gleichzeitig auftreten Schwebung N gekoppelte Oszillatoren Gleichungssystem mit = - PARAMETRISCH VERSTÄRKTE SCHWINGUNG wird als Parameter aufgefasst, der zeitlich nicht mehr konstant ist neue Bewegungsgleichung: Beispiel: Fadenpendel wird bei verkürzt und bei um wieder verlängert So wird Energie in das System gepumpt mit Optimale Energiezufuhr bei wird modulisiert parametrischer Oszi , der Parameter Kapitel VIII Nichtlineare Dynamik und Chaos - NICHTLINEARER OSZILLATOR Taylor-Entwicklung: Von sin(x) an der Stelle 0: Von cos(x) an der Stelle 0: … … Exakte BG des Fadenpendels: (Näherung ist nichtlineare DGL) Berechnung von T endet beim elliptischen Integral (nicht lösbar) Beschreibung im Phasenraum Bisher immer DGL 2.Ordnung, Überführung in System aus DGL 1.Ordnung Beschreibe Zustand des Systems durch N zeitabhängigen Größen , die zu einem Vektor Geschwindigkeit zusammengefasst werden Trajektorie Beispiel: gedämpfter harm. Oszillator, Amplitude - DUFFING-OSZILLATOR Spiegelsymmetrisches Potential: Rücktreibende Kraft: blaue Kurve: c>0 und >0 mit der Amplitude zunehmende Federkonstante magenta Kurve: c>0 und <0 mit zunehmender Amplitude nimmt Federkonstante ab graue Kurve: c<0 und <0 Doppelmuldenpotential (2 Gleichgewichtsl.) Bewegungsgleichung: entspricht BG des getriebenen Oszillators + unharmonischen Term Iterative Lösung: in DGL einsetzten Wobei n den Iterationsschritt angibt Resonanzkurve Resonanzkurve kippt bei hohen Anregungsamplituden weg (weil -Term nicht mehr vernachlässigt werden kann und deshalb wird die Frequenz, die zu einer Amplitude gehört, nach oben verschoben. Da Amplitude des getriebenen Oszillators selbst von der antreibenden Frequenz abhängt, führt das zur Asymmetrie der Resonanzkurve). Resonanzkurve hat in diesem Bereich 2 stabile und 1 instabile Lösung. Weg von kleiner zu hoher Frequenz ist nicht gleich dem Weg von hoher zu niedriger Frequenz (bei gleich hoher treibender Kraft). Hysterese-Verhalten (Zustand für einen gegebenen Satz von Parametern, treibende Frequenz w und Beschleunigung K, hängt von der Vorgeschichte des Systems ab) - Doppelmuldenpotential o Lässt man Kugel im Zentrum los, fällt sie in eine der beiden Mulden und schwingt dort relativ harmonisch (System beruhigt sich nach längerer Zeit) o Wenn antreibende Kraft groß genug ist, dann kann das System zwischen beiden Minima des Doppelmuldenpotentials hin und her getrieben werden. Es entsteht Schwingung mit zwei Frequenzen (f in den Minima und f zwischen den Minima) Periodenverdoppelung (Bifurkation) o Wenn antreibende Kraft zu groß wird, verhält sich das System chaotisch SELBSTERREGENDE SCHWINGUNG Oszillator holt sich zum selbst bestimmten Zeitpunkt Energie ab und entdämpft sich damit Van-der-Pol Oszillator Bewegungsgleichung Kleine Amplitude Dämpfung negativ (Ruhelage wird instabil, System beginnt zu schwingen) Größer werdende Amplitude nichtlinearer Term geht gegen null, Dämpfung wird positiv und kompensiert die entdämpfende Wirkung des – Terms (Energiezufuhr und Dämpfung kompensieren sich). Das System geht in Grenzzyklus über. o Bei sehr kleinem ist die Schwingung bei guter Näherung harmonisch (dauert lang) o Wenn relativ groß wird, schwingt sich das System schneller ein, weicht aber deutlich von harmonischer Schwingung ab und die Frequenz ist etwas niedriger als (bei frei ged. Oszi) o Wird zu groß gewählt, kommt man in den Bereich der Relaxationsschwingungen (System bleibt lange in einem Zustand und schaltet dann schnell in anderen Zustand…) Getriebener Van-der-Pol Oszillator Amplitude als Funktion der Zeit ähnelt der Schwebung - Phänomene: o Periodische (endliche Zahl an Durchstoßpunkten) oder quasiperiodische (Punkte bilden geschlossene Kurve) Trajektorien (sieht man im Poincaré-Schnitt) o Frequenzkamm o Synchronisation des Oszillators mit der treibenden Frequenz (Poincaré-Schnitt besteht aus einem Punkt, d.h. System oszilliert stabil mit antreibender Frequenz. Wenn Frequenzdifferenz klein ist, reicht auch kleine Kraft, damit System auf treibende Frequenz einrastet. Amplitude ändert sich kaum. Damit lässt sich starker Oszi durch schwachen Oszi auf eine Frequenz bringen) BIFURKATION, EIN WEG INS CHAOS Kapitel IX Mechanische Wellen Schwingung: harm. Oszillation eines (oder mehrerer) Körper y(t) Welle: Kopplung räumlich benachbarter Punkte Ausbreitung einer Welle y(x,t) - TRANSVERSALSCHWINGUNG EINES SEILES 2.N.G. für ein Massenelement Resultierende Kraft auf Wellengleichung mit (wenn –ct, dann geht’s in +x-Richtung) Sinusförmige (harmonische) Welle Superpositionsprinzip Sind Lösungen der Wellengleichung, dann ist auch Reflexion am festen Ende Randbedingung: Der reflektierte Puls ist invertiert Bei harmonischer Welle: Stehende Welle mit Knoten bei Reflexion am offenen Ende Randbedingung (da Bei harmonischer Welle: Stehende Welle mit Knoten bei Eigenschwingungen eines Seils o Beide Seiten geschlossen/offen o Eine Seite offen, die andere geschlossen Energietransport einer harm. Seilwelle mit Lösung - SCHALLWELLEN Longitudinalwellen in Gasen, Flüssigkeiten und Festkörpern Kraft: (Druckdifferenz) Volumenänderung: (Geschwindigkeitsdifferenz) Kompressibilität: Wellengleichung für Druck Lösung: Auslenkungsamplitude Wellengleichung für Schallschnelle Lösung: Schallgeschwindigkeit In Luft: Impedanz (Wellenwiderstand) ( Intensität Lautstärke: - AKUSTISCHER DOPPLER EFFEKT 1) Schallquelle bewegt sich mit Geschwindigkeit u Wellenlänge vor (nach) Quelle wird verkürzt (verlängert): Gemessene Frequenz vor (hinter) Quelle: 2) Beobachter bewegt sich mit Geschwindigkeit u Schallgeschwindigkeit relativ zum Beobachter: Gemessene Frequenz vor (nach) Beobachter: - MACHER KEGEL Schall wird in Konus mit Öffnungswinkel abgestrahlt )