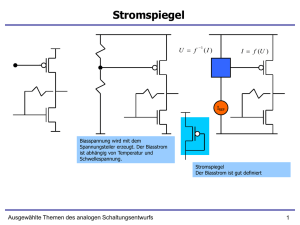
Kommutierende Operatoren

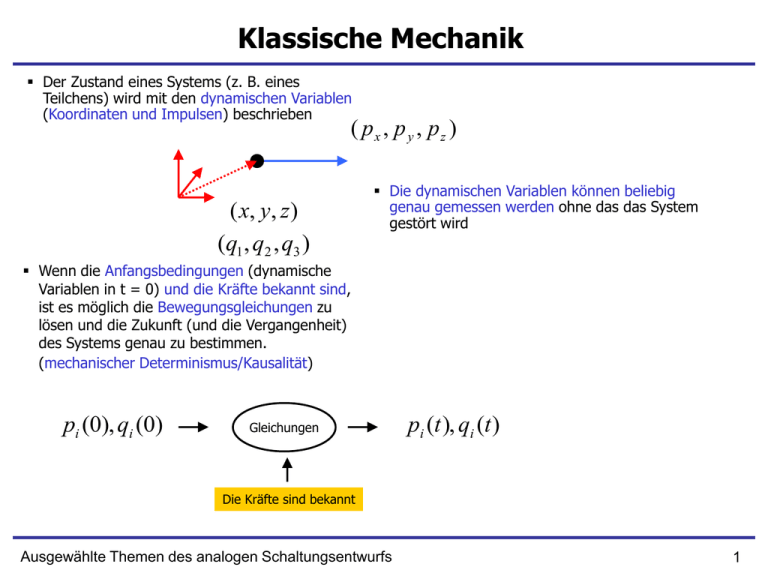
Klassische Mechanik
 Der Zustand eines Systems (z. B. eines
Teilchens) wird mit den dynamischen Variablen
(Koordinaten und Impulsen) beschrieben
( px , p y , pz )
( x, y , z )
(q1 , q2 , q3 )
 Die dynamischen Variablen können beliebig
genau gemessen werden ohne das das System
gestört wird
 Wenn die Anfangsbedingungen (dynamische
Variablen in t = 0) und die Kräfte bekannt sind,
ist es möglich die Bewegungsgleichungen zu
lösen und die Zukunft (und die Vergangenheit)
des Systems genau zu bestimmen.
(mechanischer Determinismus/Kausalität)
pi (0), qi (0)
Gleichungen
pi (t ), qi (t )
Die Kräfte sind bekannt
Ausgewählte Themen des analogen Schaltungsentwurfs
1
Newtonsche Gleichung
 Newtonsche Gleichung
mr  F
Kraft
Differentialgleichung zweiter
Ordnung, r(t) Unbekannte
Funktion
r  xe x  ye y  ze z
Beschleunigung
mx  f x , my  f y , mz  f z
 Potentielle Kraft
U=mgx
Potential
F=mg
U ( x, y, z, t )
U
U
fx  
, fy  
, fz  
x
y
z
 Konservative Kraft – Potentielle Energie ist
Zeitunabhängig
U  U (t )
Ausgewählte Themen des analogen Schaltungsentwurfs
v
x
U  mgx
dU
fx  
 mg
dx
2
Kinetische Energie
 Kinetische Energie
x(0)=0
U(0)
x(dt)=dx
U(dx)
f
1 2 1
1
2

T  mr  mv  m( x 2  y 2  z 2 )
2
2
2
dT
1 d 2
1
d


dT 
dt  m ( x )dt  m(2 x x )dt  mxdtx  mdxx
dt
2 dt
2
dt
Wegen der Newtonschen Gleichung
mxdx  f x dx  dA
 dT  dA
Mechanische Arbeit der Kraft f auf dem Weg dx = Zuwachs der kinetischen Energie
f x dx  
dU
dx   dU
dx
 dT  dU
Mechanische Arbeit = - Änderung der potentiellen Energie
Ausgewählte Themen des analogen Schaltungsentwurfs
T  U  const  E
Summe der kinetischen und
potentiellen Energie ist konstant
3
Lagrange - Funktion
L  T U
Lagrange Funktion (nichtrelativistische klassische Mechanik)
Potentielle Energie
Kinetische Energie
1 2
L  mr  U
2
1
L  m( x 2  y 2  z 2 )  U ( x, y, z )
2
Ausgewählte Themen des analogen Schaltungsentwurfs
4
Generalisierte Koordinaten
r  xe x  ye y  ze z
x
x  x(q1 ,..., qn )
x  R sin 
y  y(q1 ,..., qn )
y  R cos 
z  z (q1 ,..., qn )
r  
i
φ
y
n <= 3
x
y
z
qi e x  
qi e y  
qi e z
qi

q

q
i
i
i
i
Zwei gleiche Indizes fett geschrieben - Summe
r 
x
y
z
qi e x 
qi e y 
qi e z
qi
qi
qi
r  R cos( ) e x  R sin(  ) e y
L
1
m( ijqi q j )  U (q1 ,..., qn )
2
L
 ij   ji 
1
mR 2 2  mgR cos 
2
x x y y z z


qi q j qi q j qi q j
Ausgewählte Themen des analogen Schaltungsentwurfs
5
Wirkungsintegral und Hamiltonsches Prinzip
qi  qi (t )
qi  qi (t )
Beliebige Zeitfunktion
x(0)=0
f
Der eigentliche Weg
t0
w   L(q1 ,..., qn , q1...qn )dt
x(t0) = x0
0
Wirkungsintegral
w  0
x0
x (t )
qi (t )  qi (t )
t0
Der Wirkungsintegral hat einen Extremwert wenn q dem eigentlichen Weg gleich ist
Jede kleine Variation des q(t) ergibt in erster Ordnung δw =
0.
Ausgewählte Themen des analogen Schaltungsentwurfs
t0
1 2

w    mx  (mgx) dt
2

0
6
Lagrange Gleichungen
 L

L


w   
qi 
qi dt
qi
qi

0
t0
Wir variieren die q(t)
t0
0
L
L d (qi )
L
d  L 

qi dt


q
dt

dt


q

i
0 qi i 0 qi dt

qi
dt  qi 
0
0
t0
t0
t
δq(t0) = δq(0) = 0
t0
 L
w   
0
 qi

d  L  

 qi dt
dt  qi  
d  L  L

 
0
dt  qi  qi

q0
d  L  L

 
0
dt  qi  qi
q (t )
t0
Lagrange Gleichungen
Ausgewählte Themen des analogen Schaltungsentwurfs
7
Lagrange Gleichungen (Beispiel)
d  L  L

 
0
dt  qi  qi
L
Lagrange Gleichungen
φ
1
mR 2 2  mgR cos 
2
d  L  L


0
dt    
R  g sin   0
Ausgewählte Themen des analogen Schaltungsentwurfs
8
Hamiltonsche Gleichungen
Lagrange-Gleichung - differentialgleichung zweiter Ordnung
d  L  L

 
0
dt  qi  qi
L
pi 
qi
L
f (qi , qi , qi )  0
Wir versuchen aus LG zwei Gleichungen erster Ordnung herzuleiten…
f (qi , pi , qi )  0
f ( p i , pi , qi )  0
Kanonischer Impuls wird definiert
1
m( ijqi q j )  U (q1 ,..., qn ) 
2
pi 
1
1
m ijq j  m ji q j  m ijq j
2
2
qi  f ( p1 ,..., pn )
L  L( pi , qi )
Es ist möglich die Lagrange Funktion als Funktion von Impulsen und Koordinaten darzustellen
L
p i 
q i
Hat die Form
f ( p i , pi , qi )  0
Ausgewählte Themen des analogen Schaltungsentwurfs
Es fehlt noch…
f (qi , pi , qi )  0
9
Hamiltonsche Gleichungen (2)
pi 
p i 
L 
L
qi
L
q i
Definition – Kanonischer Impuls
f (qi , pi , qi )  0
Wir leiten die zweite Gleichung her…
Erste Gleichung
L
L
qi 
qi 
qi
qi
L  p iqi  piqi
Variieren wir Lagrange-Funktion
piqi   ( pi qi )  pi qi
 ( L  pi qi )  p iqi  qipi
H  pi qi  L
Wir definieren die Hamiltonsche Funktion
p i  
H
H
, qi 
dqi
dpi
Hamiltonsche Gleichungen
Ausgewählte Themen des analogen Schaltungsentwurfs
10
Physikalische Bedeutung der Hamiltonschen Funktion
1
L  m( ijqi q j )  U (q1 ,..., qn )
2
und
L
pi 
qi
ergibt
pi  m ij q j
Definition des Impulses
H  pi qi  L
Definition der Hamiltonschen Funktion
pi qi  m ijq jqi  2T
Zweifache kinetische Energie
H  2T  (T  U )  T  U  E
Hamiltonsche Funktion stellt die Gesamtenergie des
Systems dar
Für die Kartesische Koordinaten gilt:
q1  x, q2  y, q3  z
Daraus folgt
und
 ij   ij
Kanonische Impulse sind den gewöhnlichen Impulsen gleich
p x  mx , p y  my , p z  mz
Ausgewählte Themen des analogen Schaltungsentwurfs
11
Poisson-Klammer
u v u v
u, v  

p i q i
i q i p i
Zwei Funktionen der Kanonischen Impulse und Koordinaten
dF
F
 F , H  
dt
t
Eine nicht explizit Zeitabhängige Funktion F dynamischer Variablen p und q ändert Ihren Wert nicht wenn [F, H] = 0
F ist dann eine Konstante der Bewegung (Erhaltungsgröße)
H  H (x)   px , H   0
H , H   0
Gesamtenergie bleibt erhalten
Impulskomponente bleibt erhalten wenn in dieser Richtung keine Kraft wirkt
Ausgewählte Themen des analogen Schaltungsentwurfs
12
Lineare Vektoralgebra
Vektoren
Vektorraum
Folgendes wird definiert:
  f  ;  , f ,  E
Addition
  f ;  , f  E;   C
Multiplikation mit einer komplexen Zahl
Addition ist kommutativ
Assoziativgesetz, Distributivgesetz
1 f1  ...  n f n  0  i  0
Linearunabhängige Vektoren (Definition)
Ein Vektorraum mit nicht mehr als M linearunabhängigen Vektoren ist M-dimensional
Ausgewählte Themen des analogen Schaltungsentwurfs
13
Vektoralgebra (Skalarprodukt)
( f , g) C
Skalarprodukt (Innenprodukt) ist eine komplexe Zahl. Es gilt:
( f , g )  ( g , f )*
( f , g )   ( f , g )
(f , g )  * ( f , g )
( f , f )  2 , 2  , 2  0
λ = Norm
( f , f ) 1
Norm = 1, normierter Vektor
( f , g)  0
orthogonale Vektoren
Ein Vektorraum mit definiertem Skalarprodukt definieren wir hier als Hilbert-Raum
Ausgewählte Themen des analogen Schaltungsentwurfs
14
Darstellung des Vektors in einer Basis
  
ex , e y , ez
M Linearunabhängige Vektoren eines M-dimensionalen
Raums bilden eine Basis
f1 , ... , f M
  c1 f1  ...  cM f M
Jeder Vektor dieses Raums kann als
lineare Kombination der
Basisvektoren dargestellt werden
( f i , f j )   ij ;  ii  1,  i  j  0




r  xex  ye y  zez

ei e j   ij
Eine orthonormale Basis
Die Koeffizienten können wie folgend berechnet werden

x  ex r
ci  ( f i ,  )
Für einen normierten Vektor φ gilt
( ,  )  c1  ...  cM
2
2
1
Ausgewählte Themen des analogen Schaltungsentwurfs
x2  y2  z 2  1
15
Operator
Operator
Vektor
Aˆ f  g ,
f , g E
Aˆ ( f  g )  Aˆ f  Aˆ g
Operator (Abbildung)
Linearer Operator
Aˆ (f )  Aˆ f
Zwei Operatoren sind nicht immer
miteinander vertauschbar
Aˆ Bˆ f  Bˆ Aˆ f
 
Aˆ Bˆ  Bˆ Aˆ  Aˆ , Bˆ
Kommutator
Ausgewählte Themen des analogen Schaltungsentwurfs
16
Hermitesche Operatoren und Eigenwert
( , Aˆ f )  ( Aˆ  , f )
Aˆ  Aˆ 
ist adjungiert von
Â
ist selbstadjungiert (ähnlich wie hermitesch)
Â
Aˆ f n  an f n
Eigenwert
 
Eigenwert Problem
Eigenfunktion
Die Menge aller Eigenwerte eines
Operators bildet sein Spektrum
Das Spektrum kann diskret oder
kontinuierlich sein
Wenn mehrere Eigenvektoren
demselben Eigenwert entsprechen,
dann ist dieser Eigenwert entartet
Ausgewählte Themen des analogen Schaltungsentwurfs
17
Eigenschaften Hermitescher Operatoren
Eigenwerte eines hermiteschen Operators sind reell
Beweis:
Aˆ f n  an f n
( f n , Aˆ f n )  an ( f n , f n )  an
Konjugation
*
an  ( Aˆ f n , f n )  ( f n , Aˆ f n )  an
Eigenfunktionen mit unterschiedlichen Eigenwerten sind orthogonal
Beweis:
Aˆ f n  an f n
Aˆ f m  am f m
( f m , Aˆ f n )  an ( f m , f n )
( f n , Aˆ f m )  am ( f n , f m )
Konjugation
( Aˆ f m , f n )  am ( f m , f n )
*
am ist reell
( f m , Aˆ f n )  am ( f m , f n )
0  (an  am )( f m , f n )  0  ( f m , f n )
Ausgewählte Themen des analogen Schaltungsentwurfs
18
Kommutierende Operatoren
Einen Operator nennt man Observable wenn seine Eigenvektoren eine orthonormale Basis
darstellen.
Wenn zwei Operatoren kommutieren, haben sie wenigstens eine Menge gemeinsamer
Eigenvektoren die eine Basis bilden
Wenn zwei oder mehr Operatoren kommutieren und es gibt keinen weiteren Operator der mit ihnen
kommutiert, bilden sie einen vollständigen Satz kommutierender Operatoren. Diese Operatoren
haben eine eindeutige Menge gemeinsamer Eigenvektoren die eine Basis bildet.
Die Angabe der Eigenwerte aller dieser Operatoren ausreicht, um (bis auf einen Faktor) eindeutig einen
gemeinsamen Eigenvektor zu bestimmen.
Ausgewählte Themen des analogen Schaltungsentwurfs
19
Darstellung in einer Basis und Operator
Jede beliebige Form kann auf die Grundformen zerlegt werden
Basisvektoren
Grundformen
= 5X
+ 4X
+ 1X
Regel der Abbildung „A“
Mit 1 multiplizieren
Mit 2 multiplizieren
Mit 3 multiplizieren…
A
= 5X
+ 8X
+ 3X
Der Operator A erkennt die Grundformen und ändert ihren Anteil
Ausgewählte Themen des analogen Schaltungsentwurfs
20
Eigenwert
So werden die Basisvektoren abgebildet:
Basisvektoren
(Grundformen)
Eigenwert
A
A
Eigenvektor
1
3
Regel der Abbildung „A“
Mit 1 multiplizieren
Mit 2 multiplizieren
Mit 3 multiplizieren…
Ausgewählte Themen des analogen Schaltungsentwurfs
21
Kommutierende Operatoren
Zur Darstellung von Formen in Farbe
brauchen wir mehr Basisvektoren:
A
A
A
1
1
Entartung des Eigenwerts
„1-Viereck“
Die Angabe die Formen
reicht nicht aus um einen
Basisvektor zu definieren
1
Wir führen einen anderen Operator ein, der die Farben erkennt
Der neue Operator B kommutiert mit dem Operator A und
hat identische Eigenvektoren
B
B
B
Ausgewählte Themen des analogen Schaltungsentwurfs
Blau
Mit zwei Eigenwerten ist ein
Basisvektor eindeutig
definiert (1-Viereck, Blau)
Rot
Die zwei Operatoren bilden
einen vollständigen Satz
kommutierender
Operatoren
Gelb
22
Postulate der Quantenmechanik
Zustand eines Teilchens (Systems) wird durch einen normierten Vektor aus dem Hilbert Raum aller
Zustände beschrieben
Wenn zwei Vektoren sich nur durch die Konstante eiφ (Phase) unterscheiden, stellen sie den
gleichen Zustand dar.
Falls ein System sich in den Zuständen f1 und f2 befinden kann, ist c1 f1 + c2 f2 auch ein möglicher
Zustand dieses Systems
Dirac Notation
Ein Vektor
fi
Zustandsvektor
BracKet
fi
( f , g ) f g
Jedem Ket Vektor
fi
entspricht ein Bra Vektor
Ausgewählte Themen des analogen Schaltungsentwurfs
fi
23
Dirac-Notation
Dirac Notation
( f , g ) f g
( f ,  f )  (* f , f )
 f  * f
Für hermitesche Operatoren gilt
( Aˆ f , g )  ( f , Aˆ g )  f Aˆ g
Ausgewählte Themen des analogen Schaltungsentwurfs
24
Darstellung in Basis
Darstellung des Vektors in einer Basis
Mathematische Notation
f1 , ... , f M
Dasselbe in Dirac Notation
Zerlegung mit
Basisvektoren
  c1 f1  ...  cM f M
( f i , f j )   ij
ci  ( f i ,  )
f1 , ... , f M
  c1 f1  ...  cM f M
Basisvektoren
f i f j   ij
sind
orthonormal
ci  f i 
Dann gilt…
   f1 f1  ...  f M f M  
Iˆ   f i
fi
Einheitsoperator
i
Ausgewählte Themen des analogen Schaltungsentwurfs
25
Darstellung in Basis

r
( x, y , z )
  c1 f1  ...  cM f M
Einheitsoperatoren
 Aˆ     f i f i Aˆ f j f j 
i, j
a11  a1M   d1 

  

 
cM 1  aMM   d M 
 Â   c*1 c* M 

c
*
1
c
*
M


Bra Vektor wird durch eine Spaltenmatrix dargestellt
Ket Vektor wird durch eine Zeilenmatrix dargestellt
c1 
 
 
cM 
Matrix Form
Â
a11  a1M 




cM 1  aMM 
Operator wird durch eine quadratische Matrix dargestellt
Ausgewählte Themen des analogen Schaltungsentwurfs
26
Messgrößen und Observablen
Jeder Messgröße (dynamischer Variable) ist ein Operator (Observable) zugeordnet.
p, r  pˆ , rˆ
Zu klassischen Koordinaten und Impulsen sind Operatoren
zugeordnet
Klassische dynamische Variablen lassen sich als Funktionen
von p und x darstellen
F ( pi , xi )  F ( pˆ i , xˆi )

i ˆ ˆ
F , H    F , H


Pissson Klammer
Kommutator
 p , q    i pˆ , qˆ 
i
j
p , q   
i
j

ij
i
j
pˆ , qˆ   i
i
j
ij
Ausgewählte Themen des analogen Schaltungsentwurfs
27
Messergebnisse und Eigenwerte
Das Ergebnis der Messung einer dynamischen Variable ist ein Eigenwert der zugeordneten
Observable.
Aˆ ui  ai ui
Wenn die Observable diskretes Spektrum hat, geben die Messungen entsprechender Größe diskrete Werte.
Die Wahrscheinlichkeit im Zustand ψ den Eigenwert ai zu messen
W (ai )  ui 
2
Die Eigenvektoren einer Observable bilden eine
Basis. Deswegen kann man schreiben:
  c1 u1  ...  cM uM
Und es gilt:
W (ai )  ui 
2
 ci
Ausgewählte Themen des analogen Schaltungsentwurfs
2
Für einen Vektor mit
Norm = 1 gilt:
c1  ...  cM
2
2
1
28
Reduzierung des Wellenpakets
Aˆ ui  ai ui
Annahme: Ein System befindet sich in dem Zustand:
ui
Die Messung der Variable A gibt dann ganz sicher das Ergebnis ai
Annahme: Das System befindet sich in dem
Zustand

Die Messung der Variable A gibt Ergebnis ai. Die Messung überführt das System in den neuen
Zustand:
ui
ui 
Pˆ 
 Pˆ 
Pˆ  ui ui
Projektor
Ausgewählte Themen des analogen Schaltungsentwurfs
29
Reduzierung des Wellenpakets
FormX
Messergebnis
Wahrscheinlichkeit dass eine Messung
auf φ die FormX gibt
W  FormX 
Anfangszustand
W 1
2

FormX
FormX 
Durch die Messung wird der Zustand
des Systems in einen Eigenzustand der
Observable übeführt
Ausgewählte Themen des analogen Schaltungsentwurfs
Pˆ 
 Pˆ 
30
Kommutierende Observablen
Zu den dynamischen Variablen A und B sind zwei Observablen
zugeordnet
Aˆ , Bˆ
Wenn die Observablen kommutieren, gibt es wenigstens eine Basis gemeinsamer Eigenvektoren
Aˆ am , bn i  am am , bn
Bˆ am , bn i  bn am , bn
Dann gibt es einen Zustand
i
i
am , bn
i
Index i kennzeichnet die unterschiedlichen
Basisvektoren im Fall von Entartung. Entartung
ist ein Zeichen dafür dass es noch andere
Operatoren gibt, die mit A und B kommutieren.
A und B stellen keinen vollständigen Satz
kommutierender Operatoren
in welchem die Messung der Variable A immer das Ergebnis am und die
Messung der Variable B immer das Ergebnis bn gibt.
- Die Ergebnisse hängen von Reihenfolge der Messungen nicht ab
- Die Observablen A und B sind kompatibel.
Ausgewählte Themen des analogen Schaltungsentwurfs
31
Kommutierende Observablen
Das Messergebnis ist im voraus
bestimmt
W 1
W 1
FormX, Rot
Das System befindet sich in
dem gemeinsamen
Eigenzustand zweier
kommutierenden Operatoren
Die Messungen geben immer
die gleichen Ergebnisse, „rot“
und „FormX“
Ausgewählte Themen des analogen Schaltungsentwurfs
32
Nichtkommutierende Observablen
W  FormX 
2
W  Rot FormX ,i
2
W  FormY Rot , j
2
Die zwei Operatoren (Formund Farbenerkennung)
kommutieren hier nicht. Sie
haben keine gemeinsamen
Eigenzustände.
Jede Messung überführt das
System in den Eigenzustand
der (zu der Messgröße
zugeordneten) Observable.
Die Messergebisse können
nicht präzise vorausgesagt
werden.
Wenn die Observablen nich kommutieren, haben sie keine gemeinsamen
Eignvektoren.
Die Variablen können nicht durch wiederholte Messungen genau bestimmt
werden
Ausgewählte Themen des analogen Schaltungsentwurfs
33
Schrödinger Gleichung
Die Zeitentwicklung eines Systems wird durch die Schrödinger-Gleichung beschrieben
d
i  (t )  Hˆ  (t )
dt
Partielle Differentialgleichung
Hamiltonoperator ist eine Observable.
Sie ist der Gesamtenergie des
Systems zugeordnet.
t
Kennen den Zustand eines Systems in t = t0, dann können wir die Zeitenwicklung des
Systems berechnen.
QM Determinismus. Zeitenwicklung ist bestimmt wenn wir das System alleine lassen,
d.h. keine Messungen auf dem System durchführen.
Ausgewählte Themen des analogen Schaltungsentwurfs
34
Wellenfunktion
Koordinate ist eine Observable. Deren Eigenvektoren bilden eine Basis.
Für diskrete Eigenwerte gilt:
1) W(ai) – Wahrscheinlichkeit
dass eine Messung einen
bestimmten Wert ai gibt
2) I – Einheitsoperator
3) Vektoren sind Orthonormal
(Die Norm=1)
xˆ x0  x0 x0
Spektrum ist kontinuierlich
W (ai )  ui 
2
I (Einheitsoperator)
Iˆ   ui ui
    x x   dx
   x x  dx
ui u j   i , j
W  x
i
W ( x0 )  x0 
Die entsprechende Formel
im Fall des kontinuierlichen
Spektrums
W(x0) -Wahrscheinlichkeit
dass sich Teilchen im
Bereich (x0, x0 + dx)
befindet.
Die Norm ist mit Dirac‘scher
Delta Funktion definiert
2
dx
Iˆ   x x dx
x1 x2   ( x1  x2 )
Wir definieren die Wellenfunktion
Wellenfunktion ist Ket Vektor in
Koordinatendarstellung
Wahrscheinlichkeit dass sich das
Teilchen in der dx Umgebung von x
befindet
Ausgewählte Themen des analogen Schaltungsentwurfs
2
dx
Wahrscheinlichkeit dass sich das
Teilchen in der Umgebung von x
befindet
 ( x)  x 
 * ( x)   x
W   dx
2
35
Koordinatenoperator
Finden wir den
Koordinatenoperator in
Koordinatendarstellung
 xˆ    IˆxˆIˆ     x1 x1 xˆ x2 x2  dx1dx
2
Matrixelement des Operators x in Koordinatendarstellung
Es gilt auch:
xˆ x  x x
Eigenwert-Gleichung
x1 x2   ( x1  x2 )
Und:
 x   * ( x), x2    ( x)
 
Definition der Wellenfunktion
x1 x1 xˆ x2 x2  dx1dx    * ( x1 ) ( x1  x2 ) x2 ( x2 )dx1dx    * ( x)x ( x)dx
2
2
Koordinatenoperator in
Koordinatendarstellung
Ausgewählte Themen des analogen Schaltungsentwurfs
36
Wellenfunktion und die Wahrscheinlichkeit
Rechnen wir die Wahrscheinlichkeit aus dass
sich das Teilchen irgendwo in gesamtem Raum
befindet
*

(
x
)
dx



 ( x) ( x)dx    x x  dx     1
2
Ändert sich diese Wahrscheinlichkeit wenn man
Schrödinger Gleichung anwendet?
i
d
 (t )  Hˆ  (t0 )
dt
Schrödinger Gleichung und die Wahrscheinlichkeit
Die Norm des Vektors ändert sich nicht. Wahrscheinlichkeit für
Gesamtraum bleibt 1.
Beweis
d
d
 d

 (t )  (t )   (t )   (t )     (t )   (t )
dt
 dt
  dt

Schrödinger Gleichung für Ket Vektor
Schrödinger Gleichung für Bra Vektor
d
i  (t )  Hˆ  (t0 )
dt
d
 i  (t )  Hˆ  (t )   (t ) Hˆ
dt


d
1
 (t )  (t )  
 (t ) Hˆ  (t )   (t ) Hˆ  (t )  0
dt
i
Ausgewählte Themen des analogen Schaltungsentwurfs
H ist hermitesch
37
Wichtige Operatoren in Koordinatendarstellung
Es gilt
Koordinatenoperator
Impulsoperator
H
Koordinatendarstellung
xˆ  x
pˆ x  i
pˆ , qˆ   i
i
j
ij

x
1
2
2
2
( p x  p y  p z )  U ( x, y , z , t )
2m
Klassisch
Hamiltonfunktion/Operator

1
2
2
2
ˆ
H
( pˆ x  pˆ y  pˆ z )  U ( xˆ , yˆ , zˆ, t )
2m
Quantenmechanisch
2
2
2
2





Hˆ 
( 2  2  2 )  U ( x, y, z, t )
2m x y z
Quantenmechanisch
Ausgewählte Themen des analogen Schaltungsentwurfs
38
Schrödinger Gleichung in Koordinatendarstellung
Multiplizieren wir die beiden Seite der Gleichung mit dem unitären
Operator (Die rechte Seite zweimal…).
d
i  (t )  Hˆ  (t )
dt
Iˆ   x x dx


 d

ˆ x x  (t ) x dx dx
i

x

(
t
)
x
dx

x
H


1
2
2
1
1
2
  dt




 d

ˆ ( x , t ) ( x , t ) x dx dx
i


(
x
,
t
)
x
dx

x
x
H


1
2
2
2
1
1
2
  dt


x1 x2   ( x1  x2 )
 d

ˆ
  i dt  ( x, t )  x dx   H ( x1 , t ) ( x1 , t ) x1 dx1

d
i  ( x, t )  Hˆ ( x, t ) ( x, t )
dt

2
2
2
2





Hˆ ( x, t ) 
( 2  2  2 )  U ( x, y, z, t )
2m x y z
Schrödinger Gleichung in Koordinatendarstellung
Ausgewählte Themen des analogen Schaltungsentwurfs
Koordinaten und Zeit sind hier unabhängige
Variablen. Es gilt nicht x=x(t) wie in klassischer
Mechanik
39
Lösung der Schrödinger Gleichung
2
2
2
2





Hˆ 
( 2  2  2 )  U ( x, y, z, t )
2m x y z
d
i  ( x, t )  Hˆ  ( x, t )
dt
Finden wir die Lösung für den Fall:
U  U (t )
Potentialenergie hängt nicht explizit von der Zeit ab
Wir können die Raumkoordinaten und Zeit trennen
 ( x, t )   (t ) ( x)
i ( x)
d
 (t )   (t ) Hˆ  ( x)
dt
/  (t ) ( x)
1 d
1 ˆ
i
 (t ) 
H ( x)
 (t ) dt
 ( x)
Ausgewählte Themen des analogen Schaltungsentwurfs
40
Lösung der Schrödinger Gleichung
i
1 d
1 ˆ
 (t ) 
H (r )
 (t ) dt
 (r )
1 d
i
 (t )  En
 (t ) dt
Die linke Seite hat nur Zeit als
Variable, die rechte nur Koordinaten.
Zeit und Raumkoordinaten sind in
QM unabhängig. Beide Seiten sind
daher Konstanten (En), sonst wären
sie nicht immer und überall gleich.
1 ˆ
En 
H ( x)
 ( x)
Die Zeitabhängige Gleichung hat die einfache Lösung
 (t )  ce i t , n 
n
En

Hˆ  n,i ( x)  En n,i ( x)
 n,i ( x, t )  ceiE t /  n,i ( x)
Die koordinatenhängige Gleichung ist das
Eigenwertproblem des Hamiltonoperators.
Die Konstante En ist daher die Gesamtenergie
des Systems.
Index i kennzeichnet die unterschiedlichen Funktionen im Fall von
Entartung. Entartung ist vorhanden wenn es andere Operatoren gibt die
mit dem Hamiltonoperator kommutieren
n
Die Gesamtlösung hat die Form
Ausgewählte Themen des analogen Schaltungsentwurfs
41
Zeitentwicklung eines Systems
 n,i ( x, t )  ceiE t /  n,i ( x)
n
Hˆ  n,i ( x)  En n,i ( x)
(1)
Lösung der Schrödinger Gleichung
Finden wir die Zeitentwicklung eines Systems im Zustand beschrieben mit der Wellenfunktion φ(x) in t=0
 n ,i ( x )
sind die Eigenfunktionen der Hamiltonoperators in Koordinatendarstellung. Diese Funktionen bilden
eine Basis. Deswegen gilt:
 ( x)   cn ,i n ,i ( x)
(2)
n ,i
In Dirac Notation:



 ( x)     cn,i n,i ( x)  x dx   cn,i  n,i
n ,i
 n ,i

Die Koeffizienten können wie folgend
berechnet werden
cn ,i   n ,i    * n ,i ( x) ( x)dx
Durch Vergleich (2) mit (1) bekommen wir:
 ( x, t )   cn ,i e iE t /  n ,i ( x)
n
n ,i
Ausgewählte Themen des analogen Schaltungsentwurfs
42
Stationäre Zustände
 ( x, t )   cn,i e iE t /  n ,i ( x)
n 0
n ,i
Messung der Koordinate
Zeitenwicklung
Betrag der Wellenfunktion
 ( x, t )
1. Energiemessung
E=E0
2
 ( x, t )  e iE t /   c0i 0,i ( x)
01
i
2. Energiemessung
E=E0
Keine Zeitenwicklung
 ( x, t ) 
2
c 
0i
2
0 ,i
( x)  Const (t )
i
Ab der 1. Energiemessung befindet sich das System im Eigenzustand des Operators H. In dem Zustand ändert sich nur
die Phase das Zustandsvektors. Das hat als Folgen: 1) alle physikalischen Eigenschaften des Systems bleiben
konstant. 2) jede nachfolgende Energiemessung gibt immer dasselbe Ergebnis – den gleichen Eigenwert. Aus den Gründen
nennt man die Eigenzustände des Hamiltonoperators stationäre Zustände
Ausgewählte Themen des analogen Schaltungsentwurfs
43
Ein Test für Stabilität (Nyquist)
AF ( D) 
AOL ( D)
1  T ( D)
P( D)
AOL ( D) 
Q( D)
AF ( z ) 
T ( z) 
Verstärkung mit RK
L( D)
T ( D) 
M ( D)
P( z )
1
Q ( z ) 1  L( z )
M ( z)
L( z )
M ( z)
Die Voraussetzung: Q(z) und M(z) haben
keine Wurzel mit dem positiven Reellteil
Stabilitätsbedingung: Die
Funktion im Nenner darf keine
Wurzel in der positiven
komplexen Halbebene haben
1  T ( z)
Ausgewählte Themen des analogen Schaltungsentwurfs
44
Die komplexe Analyse
f (z )
Eine Komplexe Funktion
der komplexen Variable z
Im
f ( z )  f (a) Ableitung wird definiert
'
f (a)  lim
z a
za
e z  e x iy  e x (cos y  i sin y)
z  z ei

Log ( z)  log( z )  i
f ( z )dz  0
Die Funktion ist
Analytisch wenn die
Ableitung immer gleich
bleibt, egal von welcher
Richtung sich z zum a
nähert
z
a
Re
Einige Wichtige analytische Funktionen
Cauchy‘sche Integralformel
Definition, Nullstelle n-ter Ordnung

1 f ( z)
f (a) 
dz

2i  z  a
n!
f ( z)
(n)
f (a) 
dz
n 1

2i  ( z  a )
f ( z )  ( z  a) n g ( z ), g (a)  0, 
Definition, Polstelle p-ter Ordnung
h( z )
f ( z) 
, h(a)  0, 
p
( z  a)
Ausgewählte Themen des analogen Schaltungsentwurfs
45
Nullstellen und Polstellen
e z  e x iy  e x (cos y  i sin y)
z  z ei
Log ( z)  log( z )  i
Einige Definitionen
1 f ( z)
f (a) 
dz

2i  z  a
Cauchy
Nullstelle
h( z )
f ( z) 
, h(a)  0, 
p
( z  a)
1 f ' ( z)
dz  N  P

2i  f ( z )

 N P
2
Das Integral ist die Phasenänderung
der Funktion f(z) während der
Integration auf Kontur Γ
f ( z )  ( z  a) n g ( z ), g (a)  0, 
Es folgt:
1 d
Log ( f ( z )) dz  N  P

2i  dz
z2
z3
z1
f(z2)
f(z1)
f(z3)
Polstelle
Anzahl von Nullstellen – Anzahl von
Polstellen der Funktion f(z)
innerhalb Kontur Γ
Ausgewählte Themen des analogen Schaltungsentwurfs
Anzahl von Umdrehungen des
Phasenvektors um 0 ist N-Z
46
Nullstellen und Polstellen
1  T ( z)  1 
L( z ) M ( z )  L( z )

M ( z)
M ( z)
z3
z2
z1
1+T(z2)
1+T(z3)
1+T(z1)
Die Phasenänderung der 1+T(z) für
z auf dem Kreis ist 0
  0
Ausgewählte Themen des analogen Schaltungsentwurfs
47
Nullstellen und Polstellen
z2
z1
z2
T(z2)
1+T(z2)
T(z1)
z1
1+T(z1)
-1
1+T(z)
Ausgewählte Themen des analogen Schaltungsentwurfs
T(z)
48
Nyquist‘scher Test
z2
T(z2)
z2
T(z1)
T(z2)
-1
z1
T(z1)
z1
-1
Kreis um 0 mit R=1
Bei |T(iy0)|=1 darf die Phasenänderung T(iy0)-T(0) nicht weniger als -180 Grad sein
Ausgewählte Themen des analogen Schaltungsentwurfs
49