Folie

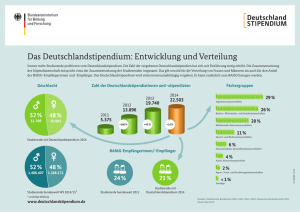
Assoziation zweier diskreter Merkmale
• Erhebung von zwei (oder mehr) Merkmalen: Frage
nach dem Zusammenhang beider Merkmale
• Sind beide Merkmale diskret mit endlich vielen
Ausprägungen (kategorial) sprechen wir von der
Assoziation
• Sind beide Merkmale stetig, sprechen wir von der
Korrelation
• Zunächst: X und Y werden als diskret
angenommen
• Statistik beantwortet nicht die Frage der Kausalität
1
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Beispiel: Körpertemperaturveränderung bei Ferkeln
Erhöhung 8
Stunden nach
Erstimpfung
Erhöhung 8 Stunden nach
Zweitimpfung
nein
ja
nein
21 (n11)
11 (n12)
32 (n1+)
3 (n21)
10 (n22)
13 (n2+)
24 (n+1)
21 (n+2)
45 (n)
ja
Summe
Summe
2
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Darstellung zweier diskreter Merkmale
• Die Darstellung der letzten Folie nennt man
Kontingenztafel
• Merkmal X: Temperaturerhöhung nach Erstimpfung
• Merkmal Y: Temperaturerhöhung nach Zweitimpfung
• Beide Merkmale sind binär und haben 2
Ausprägungen (nein/ja)
• Im Beispiel: 2x2-Tafel oder Vierfeldertafel
• Fragestellung: Sind X und Y abhängig
(assoziiert)?
3
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Definition: Unabhängigkeit
• Vorlesung vom 27.10.2005:
Zwei Ereignisse A und B heißen unabhängig, falls gilt:
P ( B | A)  P ( B )
P ( A | B )  P ( A)
P ( A  B )  P ( A)  P ( B )
4
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Unabhängigkeit zweier diskreter
Merkmale
• Jetzt: Zwei diskrete Merkmale X und Y sind
unabhängig, wenn
P( X  x, Y  y )  P( X  x) P(Y  y )
 Produkt der
Gemeinsame
Wahrscheinlichkeit
Randwahrscheinlichke iten
5
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Unabhängigkeit zweier diskreter
Merkmale II
•
•
•
•
•
Beispiel zweimaliger Münzwurf einer fairen Münze
X: Ergebnis des 1.Wurfs (K oder Z)
Y: Ergebnis des 2.Wurfs (K oder Z)
4 mögliche Kombinationen:
1. P(X=K; Y=K) = 0.25 = 0.5 · 0.5 = P(X=K) P(Y=K)
2. P(X=K; Y=Z) = 0.25 = 0.5 · 0.5 = P(X=K) P(Y=Z)
3. P(X=Z; Y=K) = 0.25 = 0.5 · 0.5 = P(X=Z) P(Y=K)
4. P(X=Z; Y=Z) = 0.25 = 0.5 · 0.5 = P(X=Z) P(Y=Z)
X und Y sind offensichtlich nach Definition unabhängig!
6
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Unabhängigkeit zweier diskreter Merkmale III
• Wahrscheinlichkeitstafel beim fairen, unabhängigen
Münzwurf:
1. Münzwurf 2. Münzwurf
Summe
K
Z
K
0.25
0.25
0.5
Z
0.25
0.25
0.5
Summe
0.5
0.5
1.0
7
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Kontingenztafel versus Wahrscheinlichkeitstafel
• Kontingenztafel: empirisch beobachtete Daten (Häufigkeiten)
• Wahrscheinlichkeitstafel: theoretische W. eines Experiments
• Münzwurfbeispiel: Fair hat nichts mit Unabhängigkeit zu tun. Unfaire
Münze (mit Wahrscheinlichkeit 0.7 kommt K):
1. Münzwurf
2. Münzwurf
K
Z
Summe
K
0.49
0.21
0.7
Summe
Z
0.21
0.09
0.3
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
0.7
0.3
1.0
8
Experiment: unfairer Münzwurf
• Das Experiment des (unabhängigen) unfairen
Münzwurfs wird 100 mal wiederholt. Wir erwarten (im
Sinne statistischer Erwartungswerte/Mittelwerte)
folgende Häufigkeiten:
1. Münzwurf
2. Münzwurf
Summe
K
Z
K
49
21
70
Z
21
9
30
Summe
70
30
100
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
9
Erwartete Häufigkeiten bei Unabhängigkeit
•
•
Die unter Unabhängigkeit von X und Y erwarteten gemeinsamen
Häufigkeiten sind das Produkt der Randhäufigkeiten geteilt durch den
Gesamtstichprobenumfang n:
(70·70 / 100) = 49 (70·30 / 100) = 21
(30·70 / 100) = 21 (30·30 / 100) = 9
Formal:
i  j
ij
e 
n n
i, j  1,2
n
eij : erwartete Häufigk.
10
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Übertragung auf das Eingangsbeispiel
Erhöhung 8
Stunden nach
Erstimpfung
Erhöhung 8 Stunden nach
Zweitimpfung
nein
21 (17.07) 11 (14.93) 32 (n1+)
ja
Summe
nein
3 (6.93)
24 (n+1)
Summe
ja
10 (6.07)
13 (n2+)
21 (n+2)
45 (n)
11
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Übertragung auf das Eingangsbeispiel II
• Berechnungsbeispiel: e_11 = (32·24) / 45 = 17.07
• Um die Assoziation von X und Y zu messen, berechnen wir den
Abstand der empirisch beobachteten Häufigkeiten von den unter
Unabhängigkeit zu erwartenden Häufigkeiten in statistisch
geeigneter Weise:
ni  n j

n 
2
2  ij
n

2
  
ni  n j
i 1 j 1
2


2
2 n  e 2
ij
ij
 

eij
i 1 j 1
n
12
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Übertragung auf das Eingangsbeispiel III

21  17.07 
 
2
2

11  14.93

2

17.07
14.93
2
2
3  6.93  10  6.07 
6.93
6.07
 6.71 (6.724 mit Computerprogramm)
13
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Pearsonscher Kontingenzkoeffizient C
C

2
 n
2
14
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Pearsonscher Kontingenzkoeffizient C (II)
• C ist ein normiertes Maß, d.h. es liegt im Intervall [0,1)
• Sind X und Y unabhängig, so gilt: C=0
• Je größer C, desto stärker die Assoziation bei gegebener
Dimension der Tafel (bis jetzt: 2x2)
• C gibt keine Richtung des Zusammenhangs an!
• C läßt sich auf IxJ-Tafeln analog erweitern (X: I Kategorien;
Y: J Kategorien)
• Im Beispiel:
6.724
C
 0.361
6.724  45
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
15
Odds Ratio
• Der Odds Ratio (das Kreuzproduktverhältnis) ist ein zu C
alternatives Zusammenhangsmaß für 2x2-Tafeln
• Der Odds Ratio gibt die Richtung des Zusammenhangs
an
• Der (empirische) Odds Ratio ist definiert als
n11n22
OR 
n12 n21
16
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Odds Ratio (II)
• Der Odds Ratio nimmt Werte im Intervall [0,∞) an
• Sind X und Y unabhängig, so ist OR=1
• Bemerkung: der OR ist nicht immer invariant gegen
Vertauschung von Zeilen oder Spalten der
Kontingenztafel
• OR>1: positive Abhängigkeit (siehe aber vorigen
Stichpunkt)
• OR<1: negative Abhängigkeit
• Im Beispiel: OR = (21·10)/(11·3) = 6.36
• Interpretation:
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
17
Interpretation des Odds Ratio (III)
nein
ja
Summe
nein
21
11
32
Ja
3
10
13
Bedingte Betrachtungen innerhalb der Zeilen:
1.Zeile (keine Temperaturerhöhung nach Erstimpfung):
Die sog. Chance (Odds), keine Temperaturerhöhung nach der
Zweitimpfung zu haben, ist
Ω1 = (21/32) / (11/32) = 21/11 = 1.91
2.Zeile (Temperaturerhöhung nach Erstimpfung):
Die sog. Chance (Odds), keine Temperaturerhöhung nach der
Zweitimpfung zu haben, ist
Ω2 = (3/13) / (10/13) = 3/10 = 0.3
18
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Interpretation des Odds Ratio (IV)
• Der Odds Ratio ist das Verhältnis der Chancen:
OR = Ω1/ Ω2 = 1.91/0.3 = 6.37
Die Chance, keine Temperaturerhöhung nach der Zweitimpfung
zu haben, ist 6.37 mal so groß für die Ferkel, die nach der
Erstimpfung keine Temperaturerhöhung hatten im Vergleich zu
den Ferkeln, die eine Temperaturerhöhung nach der
Erstimpfung hatten. Das heißt aber nicht, dass die
Wahrscheinlichkeit, keine Temperaturerhöhung nach
Zweitimpfung zu haben, für die Ferkel, die nach Erstimpfung
keine Temperaturerhöhung hatten, 6.36 mal so groß ist wie für
die Ferkel, die eine Temperaturerhöhung nach Erstimpfung
hatten, denn:
19
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Interpretation des Odds Ratio (V)
• (Bedingte) Wahrscheinlichkeit für Ferkel, die nach Erstimpfung
keine Temperaturerhöhung hatten, auch nach Zweitimpfung
keine TE zu haben, ist 21/32=0.66 und die Wahrscheinlichkeit
für die, die eine TE nach Erstimpfung hatten, ist 3/13= 0.23.
• Wichtig für Interpretation: Zeilen- und Spaltenlabels beachten.
Vertauschen wir zum Beispiel die 1. und 2. Zeile:
Ja
nein
nein
3
21
ja
10
11
Summe
13
32
OR = (3·11) / (10·21) = 0.157 = 1/6.37
Die inhaltliche Interpretation bleibt aber bei Beachtung der
Labels erhalten!
20
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Relatives Risiko
nein
ja
Summe
nein
21
11
32
Ja
3
10
13
Das (empirische) relative Risiko (RR), nach Zweitimpfung keine
TE zu haben, ist definiert als Verhältnis der bedingten relativen
Häufigkeiten (bedingt auf das Ergebnis der Erstimpfung):
n11 /( n11  n12 )
RR 
n21 /( n21  n22 )
21
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Relatives Risiko (II)
• Im Beispiel:
RR = (21/32) / (3/13) = 2.84 (≈0.66/0.23)
• Interpretation: keine Temperaturerhöhung nach
Erstimpfung „erhöht das Risiko“, auch nach
Zweitimpfung keine Temperaturerhöhung zu haben.
• RR=1 würde bedeuten: Risiko ist unabhängig vom
Ergebnis der Erstimpfung, d.h. die Merkmale TE
nach Erstimpfung und TE nach Zweitimpfung sind
unabhängig
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
22
Vor- und Nachteile des Odds Ratios
• Der Odds Ratio kann für alle gängigen
Studiendesigns berechnet werden und ist dabei
immer ein sinnvolles Zusammenhangsmaß
• Der Odds Ratio gibt die Richtung des
Zusammenhangs an (C dagegen nicht)
• Für größere als 2x2-Tafeln gibt es nicht nur einen
Odds Ratio, was die Interpretation schwierig macht.
Hier ist C ein einfacheres Assoziationsmaß
• RR ist bei manchen Studiendesigns nur in einer
bestimmten „Richtung“ anwendbar (z.B. case-control)
23
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Zusammenfassung I (was Sie wissen sollten)
• Für zwei diskrete Merkmale haben wir drei
Assoziationsmaße kennengelernt: C, Odds Ratio und
RR
• Insbesondere für 2x2-Tafeln ist der Odds Ratio ein
geeignetes Zusammenhangsmaß, da er auch eine
Richtung angibt
• Für allgemeine IxJ-Tafeln (I>2 und/oder J>2) bietet
sich C als (richtungsloses) Zusammenhangsmaß an
• Bei Verwendung des relativen Risikos RR ist auf das
Studiendesign zu achten, um keinen unsinnigen Wert
zu berechnen!
24
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005
Zusammenfassung II (was Sie können sollten)
• C berechnen
• Odds Ratio berechnen und interpretieren
• Relatives Risiko berechnen und interpretieren
25
Vorlesung: Biometrie für Studierende
der Veterinärmedizin 8.12.2005