Graphikhardware

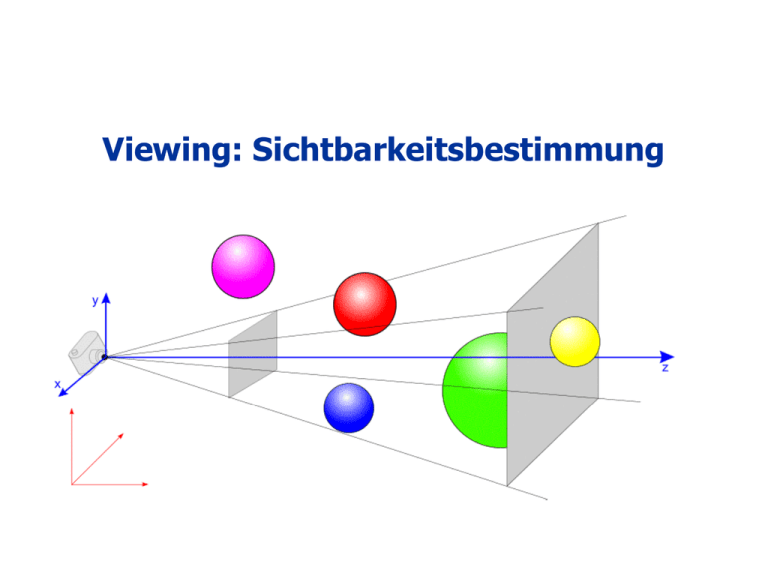
Viewing: Sichtbarkeitsbestimmung
Rendering: Einführung
• Ziel:
Integration von Einzeltechniken in ein
System zur Bilderzeugung aus einem 3D-Modell.
• Große Teile: Viewing, Shading und Rasterisierung
• Bilderzeugung = Rendering
Gegeben: ein Modell in 3D-Koordinaten sowie eine
Sicht auf die Szene (Kameramodell).
Gesucht: Pixelbild, das das gegebene Modell
realitätsnah darstellt.
B. Preim AG Visualisierung Viewing
2
Die Rendering-Pipeline
• Bilderzeugung setzt sich aus verschiedenen
Teilprozessen zusammen, die aufeinander aufbauen.
– Modellierung von 3D-Objekten
– Zusammenbau der Szene (Geometrie + Licht + Kamera)
– Entfernen nicht benötigter Modellteile (Rückseiten und alle
Objekte, die außerhalb des Sichtkörpers liegen)
– Projektion
– Entfernen von unsichtbaren Flächen (Verdeckungen)
– Beleuchtung (Shading)
– Rasterung
B. Preim AG Visualisierung Viewing
3
Die Rendering-Pipeline
Vor 14 Tagen
Modellierung
der Geometrie
Transformation in
Weltkoordinaten
(Aufbau der Szene)
Letzte Woche
Platzieren von
Kamera
und Lichtquellen
Transformation
in Kamerakoordinaten
(bestimmt durch Position und
Orientierung der Kamera)
Letzte Woche
Entfernen
verdeckter Rückseiten
Projektion
(bestimmt durch
Attribute der Kamera)
Clipping gegen
den Sichtkörper
Heute
Entfernen verdeckter
Modellteile (HSR)
Rasterung
Beleuchtungsberechnung
und Shading
B. Preim AG Visualisierung Viewing
4
Geometrische Modelle
Ausgangspunkt für das Rendering
• Rechnerinterne Darstellung der Oberfläche
• Verschiedene Modellierungsverfahren
– Explizite Repräsentation
• Angabe von Eckpunkten, Flächen, etc.
– Implizite / analytische Repräsentation
• Angabe einer mathematischen Beschreibung
(z.B. Kugel mit Radius r: x²+y²+z²-r² =0)
• Angabe eines Algorithmus‘
• Graphik I: Konzentration auf polygonale
Oberflächenmodelle
• Analytische und implizite Darstellungen lassen sich in
explizite Darstellungen umwandeln (Polygonalisieren).
B. Preim AG Visualisierung Viewing
5
Geometrische Modelle: Polygonale Modelle
• Ein 3D-Objekt wird durch ein Gitter aus polygonalen
Facetten angenähert und beschrieben.
Eckpunkte
Kanten
B. Preim AG Visualisierung Viewing Polygone
Original-Objekt Oberflächen
polygonale
Oberfläche
6
Geometrische Modelle: Polygonale Modelle
Umwandlung von analytischen/impliziten Beschreibungen in
polygonale Modelle ist mit einem Verlust an Genauigkeit
verbunden.
• Beispiele:
–
Polygonalisierung von Kugeln, Zylindern, Bezierkurven, …
• Kompromiss zwischen dem Wunsch nach hoher Genauigkeit
(Qualität) und „kleinen“ Modellen (Geschwindigkeit)
• Kompromiss ist oft einstellbar für den Anwendungsentwickler
durch Angabe eines Wertes zwischen 0 und 1 (höchstmögliche
Qualität)
• Polygonalisierung von Zylindern:
Qualität 0: Darstellung der Grundfläche als Dreieck
Qualität 1: Darstellung der Grundfläche als 20-eck
B. Preim AG Visualisierung Viewing
7
Geometrische Modelle: Polygonale Modelle
Unterschiedliche Polygonalisierungen eines Zylinders
B. Preim AG Visualisierung Viewing
8
Geometrische Modelle
Vorteile von polygonalen Modellen:
• Einheitliche Behandlung aller geometrischer Modelle
• Relativ einfache Algorithmen → daher
Implementierung in Hardware möglich
• Wichtig: Polygone müssen in einer Ebene liegen (z.B.
um zu bestimmen, was im Inneren liegt). Bei Dreiecken immer der Fall. Daher: intern Triangulierung.
B. Preim AG Visualisierung Viewing
9
Geometrische Modelle: Polygonale Modelle
•
Definition eines Polygons:
1. Angabe der Koordinaten der Eckpunkte
– x-, y-, z-Koordinatentripel
– Verbindung der Eckpunkte zu einem Polygon wird implizit
hergestellt:
– Verbinde den i-ten Punkt mit dem (i+1)-ten
– Verbinde den letzten mit dem ersten zum Schließen des Polygons
P1
P2
P3
P4
P5
P6
y
x
z
(0,0,0)-(1,0,0)- (1,1,0)- (0,1,0)
(0,0,0)-(0,0,-1)- (0,1,-1)- (0,1,0)
(0,0,0)-(1,0,0)- (1,0,-1)- (0,0,-1)
(1,0,0)-(1,0,-1)- (1,1,-1)- (1,1,0)
(0,1,0)-(1,1,0)- (1,1,-1)- (0,1,-1)
(0,0,-1)-(1,0,-1)-(1,1,-1)- (0,1,-1)
P1 und P6 liegen in der xy-Ebene.
P2 und P4 liegen in der yz-Ebene.
P3 und P5 liegen in der xz-Ebene.
B. Preim AG Visualisierung Viewing
10
Geometrische Modelle: Polygonale Modelle
2. Auflistung aller Eckpunkte (vertices) in einer Liste
– Verbindung wird angegeben durch eine Liste von Indizes
(Kanten definiert als indizierte Eckpunktliste)
Nr.
1
2
3
4
5
6
7
8
Koord.
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(0,0,-1)
(1,0,-1)
(1,1,-1)
(0,1,-1)
P1
P2
P3
P4
P5
P6
1-2-3-4
1-5-8-4
1-2-6-5
2-6-7-3
4-3-7-8
5-6-7-8
– Vorteil: kompakte Speicherung (keine Redundanz),
Projektion/Transformation des Modells: Iteration über alle
Eckpunkte
3. Weitere komplexere Modellierungstechniken
B. Preim AG Visualisierung Viewing
11
Geometrische Modelle: Polygonale Modelle
Vorteile:
• Einfache Darstellung der Objekte
• Einfache und einheitliche Handhabung bei
Berechnungen
• Weit verbreitet – „kleinster gemeinsamer Nenner“ bei
3D-Modellen
Nachteile:
• Polygonale Modelle approximieren die Oberfläche
eines „runden“ Objektes.
• Je genauer diese Approximation sein soll, um so
mehr Polygone werden benötigt – speicheraufwändig
B. Preim AG Visualisierung Viewing
12
Zusammenbau der Szene
• Bisher sind Objekte in lokalen Koordinaten gegeben, d.h. jedes
Objekt hat sein eigenes Koordinatensystem.
• Berechnungen, die mehrere Objekte einbeziehen, sind schwierig
 Transformation in ein gemeinsames Koordinatensystem
notwendig
• Weltkoordinaten
• Platzieren der Objekte
in einem globalen Koordinatensystem, in dem auch
Kameras und Lichter sowie
Oberflächeneigenschaften
der Objekte definiert werden
B. Preim AG Visualisierung Viewing
13
Zusammenbau der Szene
B. Preim AG Visualisierung Viewing
14
Zusammenbau der Szene
Wie entsteht ein größeres geometrisches Modell?
• Durch explizite Modellierung verschiedener Teile (oft
durch mehrere Personen parallel durchgeführt)
• Durch extensive Wiederverwendung von Teilen (auch
aus anderen Modellen)
• Wiederverwendung durch Kopieren, Verschieben,
Rotieren von Modellteilen (Beispiele: Räder und
Türgriffe an Autos, Fenster, Türen an Gebäuden, …)
• Repräsentation großer Modelle:
– Mehrfach verwendete Geometrie oft nur einmalig
repräsentiert; zusammen mit mehreren Transformationen
B. Preim AG Visualisierung Viewing
15
Definition Kamera(s) und Lichtquelle(n)
• Kameramodell:
– Position und Richtung
– die Abbildung bestimmende Parameter
• Lichtquellen (LQ)
– Üblich: Punktlichtquellen (LQ ohne Ausdehnung, die in alle
Richtungen gleichstark abstrahlen) – vereinfachtes Modell
• Position
• Farbe des ausgestrahlten Lichtes
• Helligkeit
– Weitere Typen von Lichtquellen möglich:
• Flächige LQ
• Gerichtete LQ (parallele Strahlen in eine Richtung)
• Spotlights
(Gerichtete LQ mit Öffnungswinkel)
B. Preim AG Visualisierung Viewing
16
Kamerakoordinatensystem
• Koordinatensystem, bei dem die Kamera im Ursprung
steht und entlang der (negativen) z-Achse
ausgerichtet ist.
• Definition des Sichtkörpers
• Einige Operationen lassen sich hier sehr einfach
ausführen, daher dieser „Zwischenschritt“
– Entfernen verdeckter Rückseiten
– Clipping gegen den Sichtkörper
B. Preim AG Visualisierung Viewing
17
Kamerakoordinatensystem
Sichtkörper bei perspektivischer Projektion begrenzt
durch 2 Ebenen (near und far)
B. Preim AG Visualisierung Viewing
18
Kamerakoordinatensystem
• Abbildung von Weltkoordinaten (des Modells) in
Kamerakoordinaten:
Model-View-Matrix.
• Matrix in homogenen Koordinaten, wird mit
Projektionsmatrix multipliziert.
Quelle: Angel (2000)
B. Preim AG Visualisierung Viewing
19
Sichtbarkeitsbestimmung:
Entfernen verdeckter Rückseiten
• Polygone entfernen, die vom Betrachter wegzeigen
(Rückseiten), da sie mit Sicherheit nicht sichtbar sind
(engl.: back face culling)
• Generelles CG-Prinzip: Versuche mit einem schnellen
(einfachen) Test eine aufwändigere Berechnung in
vielen Fällen einzusparen.
B. Preim AG Visualisierung Viewing
20
Sichtbarkeitsbestimmung:
Entfernen verdeckter Rückseiten
• Einfacher Test auf Sichtbarkeit eines Polygons mit
Hilfe von:
– Polygonnormale Np (nach außen zeigend)
– Vektor v(iew) vom Polygon zum Betrachterstandpunkt
Np
V
• Ist der Winkel > 90°, dann zeigt die Normale (und
damit die Außenseite des Polygons) vom Betrachter
weg und das Polygon ist nicht sichtbar.
B. Preim AG Visualisierung Viewing
21
Sichtbarkeitsbestimmung:
Entfernen verdeckter Rückseiten
Backface Culling (Eliminieren von Polygonen mit einer
vom Betrachter abgewandten Normale)
Erster Schritt beim Entfernen verdeckter Polygone
• Vorgehen:
– Bilde Skalarprodukt aus NpV
– Polygon ist prinzipiell sichtbar, wenn NpV>0
(und damit cos zwischen beiden Vektoren < 90 Grad.
Vorzeichentest ist schneller als Winkelberechnung)
– wichtig: Vektoren vorher normalisieren
• Einfacher Test, weil Betrachterstandpunkt im
Ursprung des Kamerakoordinatensystems
• Back face culling entfernt ~ 50% aller Polygone.
B. Preim AG Visualisierung Viewing
22
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
• Bestimmen der Teile des Modells, die nicht von
anderen Teilen des Modells verdeckt werden (oder
der Teile, die verdeckt werden) (Hidden Line bzw.
Hidden Surface Removal)
B. Preim AG Visualisierung Viewing
23
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
• Viele Verfahren zur Lösung der Aufgabe:
– Unterschiedliche Herangehensweise
• mit Objektgenauigkeit
• mit Pixelgenauigkeit
(d.h. analytische Verfahren in 3D)
(d.h. Verfahren in „2D“)
– Unterschiedliche Komplexität
– Unterschiedliche Algorithmenklassen
– Keine detaillierte Behandlung hier, nur depth-sort und zBuffer-Algorithmus (später)
B. Preim AG Visualisierung Viewing
24
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
• Aus dem Kamarakoordinatensystem werden die
Koordinaten in der (2D-)Bildebene berechnet
• Projektionstransformation (Vorlesung 6)
• Änderung zu den bisher behandelten
Transformationen: z-Werte bleiben erhalten, so dass
jeder Objektpunkt einen Tiefenwert besitzt.
• Tiefenwerte werden für das Entfernen verdeckter
Teile des Modelles beim z-Buffer-Algorithmus
benötigt.
B. Preim AG Visualisierung Viewing
25
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
Mögliche Konstellationen zwischen den Polygonen A und B:
•
•
•
•
B vor A und Projektion B und A überlappt (B verdeckt A teilweise)
A vor B und Projektion A und B überlappt (A verdeckt B teilweise)
Projektion von A und B überlappt nicht (beide komplett sichtbar)
Ein Polygon vor dem anderen und Projektion des vorderen umschließt
Projektion des hinteren (hinteres Polygon komplett verdeckt)
• Projektion des vorderen Polygones komplett in der Projektion des
hinteren enthalten (vorderes Polygon wird „über“ das hintere
gezeichnet.)
B. Preim AG Visualisierung Viewing
26
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
Depth-Sort (Objektbasierter Algorithmus)
• Sortieren der Polygone nach ihrer Entfernung zum cop
• Zeichnen von hinten nach vorn
• Problem: Bei Polygonen, bei denen sich die Abstände
zum cop und die Projektion überlappen, ist die
Zeichenreihenfolge unklar.
• Lösung: Teile solche Polygone solange bis Polygonteile
entstehen, die sich eindeutig sortieren lassen.
Dreiecke: Schwerpunkt bilden; 3 kleinere
Dreiecke konstruieren
B. Preim AG Visualisierung Viewing
27
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
Z-Buffer-Algorithmus
• Effizienter Algorithmus zum Erkennen der sichtbaren
Teile einer Szene, der in Bildschirmkoordinaten
arbeitet (besser: im Bildraum)
• Ist in Hardware implementiert (NVidia, ATI, …).
• Voraussetzung: Alle Polygone liegen transformiert vor,
wobei die Bildschirmkoordinaten eine trans-formierte
z-Koordinate besitzen, die die Tiefe angibt.
• Technische Voraussetzung: zwei „Bitmaps“
– Framebuffer enthält das eigentliche Bild
– Z-Buffer enthält Tiefenwerte
B. Preim AG Visualisierung Viewing
28
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
Algorithmus
1. Fülle den Framebuffer mit der Hintergrundfarbe
2. Fülle den z-Buffer mit der maximal möglichen Tiefe
3. Zeichne alle Polygone nacheinander:
a) Bestimme für jeden Punkt des Polygons die Position im Bild, die Farbe und
den Tiefenwert
b) Vergleiche den Tiefenwert an der Position mit dem, der dort im z-Buffer
gespeichert ist
c) Wenn der Tiefenwert des Polygonpunktes kleiner ist (weiter vorne), dann
zeichne die Farbe in den Framebuffer und setze den Tiefenwert im zBuffer auf den neuen Tiefenwert, sonst wird nichts verändert
Was heißt “jeder Punkt des Polygons”? Polygon wird abgetastet;
Berechnung wird für diskrete Punkte des Polygons durchgeführt.
Abtastrate hängt von der Größe des projizierten Polygones ab.
B. Preim AG Visualisierung Viewing
29
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
Z-buffer
B. Preim AG Visualisierung Viewing
30
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
OpenGL-Realisierung:
glutInitDisplayMode (GLUT_DOUBLE| GLUT_RGB|
GLUT_DEPTH);
glEnable (GL_DEPTH_TEST);
glClear (GL_DEPTH_BUFFER_BIT);
B. Preim AG Visualisierung Viewing
31
Sichtbarkeitsbestimmung:
Entfernen verdeckter Kanten/Flächen
Probleme bei der Sichtbarkeitsbestimmung:
• Zyklisch überlappende Polygone
• Ein Polygon „zersticht“ ein anderes (engl. Piercing).
Lösung: Teilen in solche Polygone, die sich eindeutig in
Tiefenrichtung sortieren lassen (schwierig)
Quelle: Angel (2000)
B. Preim AG Visualisierung Viewing
32
Zusammenfassung
• Entfernen von Rückseiten der Polygone
(Normale und Vektor zur Kamera betrachten)
• Entfernen verdeckter Flächen(teile) durch bildbasierte
oder objektbasierte Algorithmen
• Beispiele:
– Objektbasiert:
Sortierung der Polygone nach Abstand zur
Kamera (Sortierreihenfolge nicht immer eindeutig)
– Bildbasiert:
z-Buffer
B. Preim AG Visualisierung Viewing
33
Ausblick: Rasterung und Shading
• Nach der Projektion sind die Eckpunkte der Polygone
in Bildschirmkoordinaten gegeben.
• Noch zu tun:
– Umsetzung dieser Koordinaten auf Pixelpositionen
– Bestimmen der entsprechenden Farbe des Pixels
– „Zeichnen“ der Objekte = Rasterung
• Farbe des Pixels ist abhängig von:
– Einfallendem Licht in der 3D-Szene
– Material und Oberflächeneigenschaft der Objekte
– Betrachterstandpunkt
• Bestimmen der Farbe an einem Punkt im 3D-Modell
über Beleuchtungsmodelle, Umsetzen auf Pixelfarbe:
Shading
B. Preim AG Visualisierung Viewing
34