5.5 Elektrisches Zentralfeld, Coulombsches Gesetz

5 Elektrizität und Magnetismus
5.5 Elektrisches Zentralfeld, Coulombsches Gesetz
Elektrisches Zentralfeld
Kugel mit Radius r um eine Punktladung Q
I
I
~
~
⇒
Q = ǫ0
EdA = ǫ0 E dA = ǫ0 E(4πr2 )
(5.26)
~ A
~
Ekd
Kugel
Q
~er
4πǫ0 r2
~r
: Einheitsvektor in radialer Richtung
mit ~er =
|~r|
Zr
~ r= Q
⇒ ϕ = − Ed~
4πǫ0 r
~ =
⇒E
(5.27)
(5.28)
(5.29)
∞
Diese Gleichungen gelten auch für eine elektrisch geladene Kugel (Radius R) sofern r ≥ R
ist.
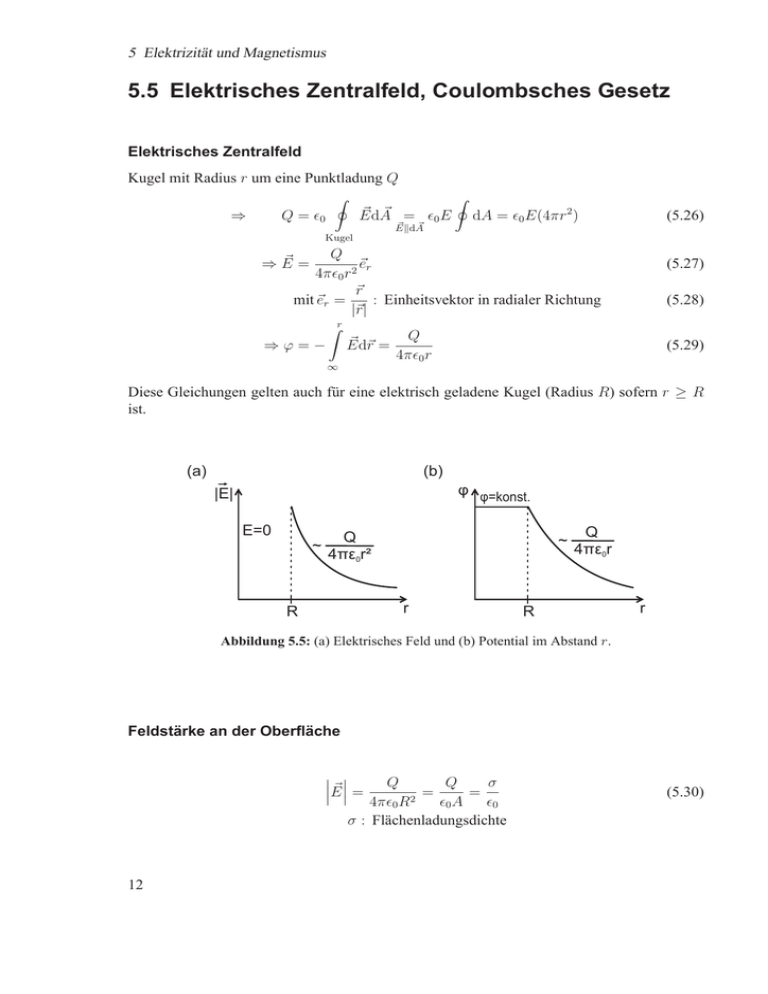
(a)
(b)
φ φ=konst.
|E|
E=0
~
Q
4πε0r²
~
r
R
Q
4πε0r
R
r
Abbildung 5.5: (a) Elektrisches Feld und (b) Potential im Abstand r.
Feldstärke an der Oberfläche
~
E =
Q
Q
σ
=
=
2
4πǫ0 R
ǫ0 A
ǫ0
σ : Flächenladungsdichte
12
(5.30)
5.5 Elektrisches Zentralfeld, Coulombsches Gesetz
Coulombsches Gesetz, Kraftwirkung zwischen zwei Ladungen
qQ
~er
4πǫ0 r2
gleiches Vorzeichen → Abstoßung
q, Q :
ungleiche Vorzeichen → Anziehung
~ =
F~ = q E
Gravitationsfeld
elektrisches Feld
Kraft
Massenanziehungskraft
(Gravitationskraft)
m1 m2
F~Gr = γ 2 ~r0
r
F~
F~Gr = m~g ; ~g =
m
Ladungsanziehungskraft
(Columbkraft)
1 Q1 Q2
~r0
F~el =
4πǫ0 r2
~
~ E
~ = Fel
F~el = QE;
Q
Energie
WGr = mϕGr
Wel = Qϕel
Potentialänderung
dϕGr = −~g d~y
~ d~y
dϕel = −E
Potentiallinien
Linien gleicher potentieller Energie
(Höhenlinien)
~g = −grad ϕGr
Linien gleichen elektrischen Potentials
(Äquipotentiallinien)
~ = −grad ϕel
E
Teilchenbeschleunigung
senkrecht zu den Höhenlinien in Richtung des
steilsten Abfalls
senkrecht zu den Äquipotentiallinien in Richtung der größten Potentialänderung
Höhenlinien
Feldlinien
Veranschaulichung
Falllinien
(5.31)
Äquipotentiallinien
Tabelle 5.1: Ähnlichkeiten zwischen Gravitationsfeld und elektrischem Feld.
13
5 Elektrizität und Magnetismus
5.6 Kapazität, Kondensatoren (Ladungsspeicher)
Leitende Kugel mit Ladung Q und Radius R:
Potential:
Q
;
4πǫ0 R
ϕ=
ϕ(∞) = 0 (Bezugspunkt)
(5.32)
Q
Q
=
4πǫ0 R
C
(5.33)
Spannung:
U = ϕ(R) − ϕ(∞) = ϕ(R) =
Kapazität:
C=
Q
= 4πǫ0 R
U
(Kapazität einer Kugel)
(5.34)
Coulomb
C
= = 1 F (Farad)
Volt
V
(5.35)
allgemein:
C=
Q
U
mit
[C] =
Die Kapazität bezeichnet das Fassungsvermögen eines elektrischen Leiters für elektrische Ladungen bei einer bestimmten Spannung.
Plattenkondensator
+ + + + + +
E
+
- - - - - -
-U
Abbildung 5.6: Wie bei der Influenz, nur dass die beiden Platten jetzt mit einer Spannungsquelle
aufgeladen werden.
Als Ladung eines Kondensators ist diejenige definiert, die eine Platte trägt.
U
d
mit d: Plattenabstand; A: Plattenfläche
E=
14
(5.36)
5.7 Parallel- und Reihenschaltung von Kondensatoren
Q = ǫ0
I
P latte
~ A
~ = ǫ0 E
Ed
|{z}
~ A
~
E||d
⇒ Q = ǫ0 EA =
⇒C=
ǫ0 A
d
I
dA
ǫ0 A
U = CU
d
Kapazität eines Plattenkondensators
(5.37)
(5.38)
(5.39)
5.7 Parallel- und Reihenschaltung von Kondensatoren
a) parallel
C1
+
C2
-
U
Abbildung 5.7: Parallelschaltung zweier Kondensatoren.
Gleiche Spannungen an C1 und C2 .
U
Q1
⇒ Qges
⇔ Qges
⇔ Qges
⇔ Cges
allgemein ⇒ Cges
= U1 = U2
= C1 U, Q2 = C2 U
= Q1 + Q2
= U (C1 + C2 )
= U Cges
= C1 + C2
X
=
Ci
(5.40)
(5.41)
(5.42)
(5.43)
(5.44)
(5.45)
(5.46)
i
b) seriell
Spannung liegt nur an den jeweils äußeren Platten an; die inneren Kondensatorplatten laden
sich durch Influenz auf.
⇒ Q1 = Q2 = Q
(5.47)
(5.48)
15
5 Elektrizität und Magnetismus
+
C1
C2
-
U
Abbildung 5.8: Reihenschaltung zweier Kondensatoren.
Spannungen addieren sich:
⇒ Uges = U1 + U2
Q
Q
U1 =
,
U2 =
C1
C2
Q
Q
⇔ Uges =
+
C1 C2
1
1
⇔ Uges = Q
+
C1 C2
1
⇔ Uges = Q
Cges
1
1
1
⇒
=
+
Cges
C1 C2
X
1
1
allgemein ⇒
=
Cges
Ci
i
Energieinhalt eines geladenen Kondensators:
Arbeit:
Z
Z
~
~ s = QU
W = F d~s |{z}
= Q Ed~
| {z }
F =QE
(5.49)
(5.50)
(5.51)
(5.52)
(5.53)
(5.54)
(5.55)
(5.56)
U
Erhöhung der Ladung um dQ erfordert Arbeit dW
Q
⇒ dW = U dQ, U =
C
(5.57)
Gesamtarbeit:
W =
Z
dW =
ZQ
0
1
U (Q )dQ =
C
′
′
ZQ
Q′ dQ′
(5.58)
0
2
1Q
1
= CU 2
2C
2
Gilt allgemein für Kondensatoren.
⇒W =
16
(5.59)
5.8 Elektrische Isolatoren
Energiedichte des elektrischen Feldes:
ωel =
Wel
1
= ǫ0 E 2
V
2
(5.60)
mit:
A
d
U = Ed
1
⇒ W = ǫ0 E 2 Ad
2
C = ǫ0
(5.61)
(5.62)
(5.63)
5.8 Elektrische Isolatoren
~ 0 eine
Da Materie aus geladenen Teilchen besteht besteht, bewirkt ein elektrisches Feld E
entgegengesetzte Kraftwirkung auf positiv und negativ geladene Teilchen und bewirkt damit
eine elektrische Polarisation.
Mechanismen:
a) Verschiebungspolarisation:
-
+ + + +
+ + + +
+ + + +
+
-
P
-
-
E0
Abbildung 5.9: Verschiebungspolarisation.
• äußeres Feld E~0
• Gegenfeld durch Polarisation P~
~ im Dielektrikum geringer
• Restfeld E
~ = E~0 − 1 P~
E
ǫ0
(5.64)
17
5 Elektrizität und Magnetismus
im Dielektrikum wird ein Dipolmoment p~ erzeugt.
~0
p~ = αE
α: Polarisierbarkeit
(5.65)
(5.66)
P~ = nαE~0 ;
n: Dipoldichte
(5.67)
Polarisation:
Aufgrund der Polarisation des Dielektrikums wird die Kapazität des Kondensators erhöht.
C = ǫC0
(5.68)
mit der Dielektrizitätskonstante ǫ (Materialeigenschaft, ǫ ≥ 1)
Luft
Wasser
Keramik
ǫ
1.0006
81
10 - 104
Feld im Dielektrikum:
~ =E
~ 0 − 1 P~ ,
E
ǫ0
~ = ǫE
~ − 1 P~
⇒E
ǫ0
~
⇔ P~ = ǫ0 (ǫ − 1)E
~ 0 = ǫE
~
mit E
(5.69)
(5.70)
(5.71)
~ wird um die Dielektrizitätskonstante erweitert:
Die dielektrische Verschiebungsdichte D
~ = ǫ0 ǫE
~ = ǫ0 E
~ + P~
D
(5.72)
Sie gibt die durch das äußere Feld verschobene Ladungsdichte an.
b) Orientierungspolarisation:
Besitzt ein Stoff schon im feldfreien Raum ein Dipolmoment, so werden diese statistisch ungeordneten Dipole im E~0 -Feld ausgerichtet.
• temperaturabhängig; je kleiner T desto besser die Orientierung
• Ausrichtung braucht Zeit; in hochfrequenten Feldern gibt es dielektrische Verluste.
18