Mechanik der Punktmassen

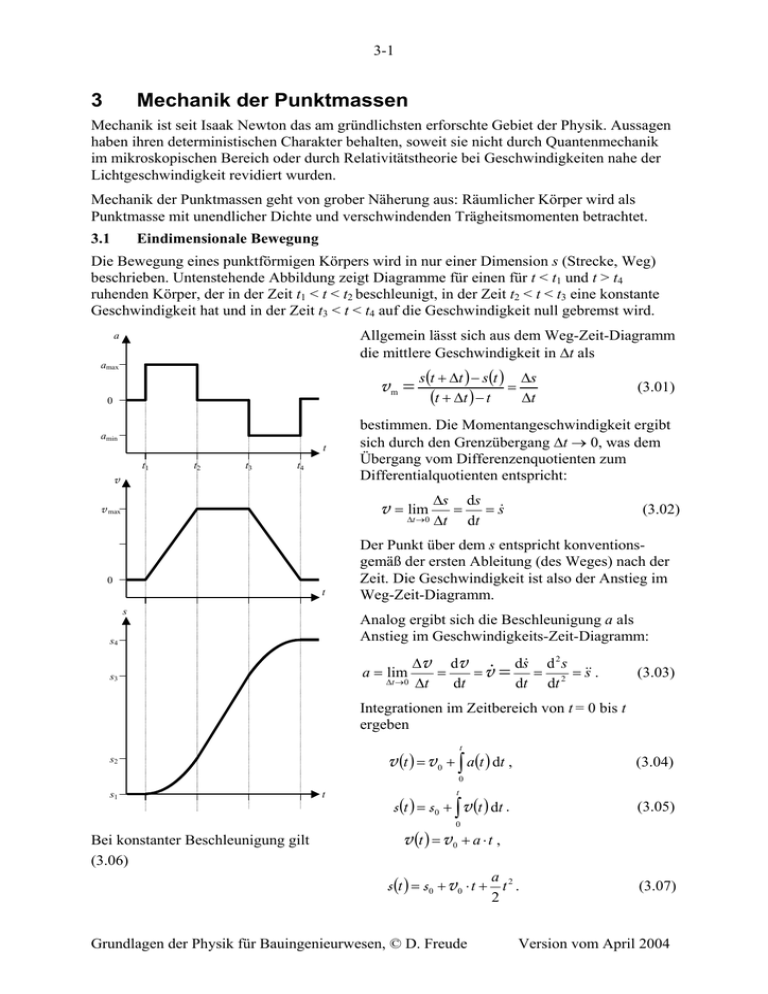
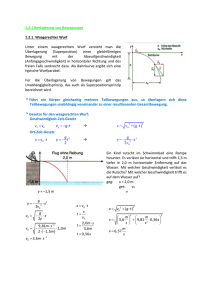
3-1
3
Mechanik der Punktmassen
Mechanik ist seit Isaak Newton das am gründlichsten erforschte Gebiet der Physik. Aussagen
haben ihren deterministischen Charakter behalten, soweit sie nicht durch Quantenmechanik
im mikroskopischen Bereich oder durch Relativitätstheorie bei Geschwindigkeiten nahe der
Lichtgeschwindigkeit revidiert wurden.
Mechanik der Punktmassen geht von grober Näherung aus: Räumlicher Körper wird als
Punktmasse mit unendlicher Dichte und verschwindenden Trägheitsmomenten betrachtet.
3.1
Eindimensionale Bewegung
Die Bewegung eines punktförmigen Körpers wird in nur einer Dimension s (Strecke, Weg)
beschrieben. Untenstehende Abbildung zeigt Diagramme für einen für t < t1 und t > t4
ruhenden Körper, der in der Zeit t1 < t < t2 beschleunigt, in der Zeit t2 < t < t3 eine konstante
Geschwindigkeit hat und in der Zeit t3 < t < t4 auf die Geschwindigkeit null gebremst wird.
a
Allgemein lässt sich aus dem Weg-Zeit-Diagramm
die mittlere Geschwindigkeit in ∆t als
amax
v m = s(t + ∆t ) − s(t ) = ∆s
(t + ∆t ) − t
∆t
0
amin
t
t1
t2
t3
t4
v
bestimmen. Die Momentangeschwindigkeit ergibt
sich durch den Grenzübergang ∆t → 0, was dem
Übergang vom Differenzenquotienten zum
Differentialquotienten entspricht:
∆s ds
v = ∆lim
=
= s&
t →0
v max
∆t
0
t
s
(3.01)
(3.02)
dt
Der Punkt über dem s entspricht konventionsgemäß der ersten Ableitung (des Weges) nach der
Zeit. Die Geschwindigkeit ist also der Anstieg im
Weg-Zeit-Diagramm.
s4
Analog ergibt sich die Beschleunigung a als
Anstieg im Geschwindigkeits-Zeit-Diagramm:
s3
a = lim
∆v dv
ds& d 2 s
=
= v& =
=
= &s& .
∆t →0 ∆t
dt
dt dt 2
(3.03)
Integrationen im Zeitbereich von t = 0 bis t
ergeben
t
v (t ) = v 0 + ∫ a(t ) dt ,
s2
(3.04)
0
s1
t
t
s (t ) = s 0 + ∫ v (t ) dt .
(3.05)
0
Bei konstanter Beschleunigung gilt
(3.06)
v (t ) = v 0 + a ⋅ t ,
a
s (t ) = s 0 + v 0 ⋅ t + t 2 .
2
Grundlagen der Physik für Bauingenieurwesen, © D. Freude
(3.07)
Version vom April 2004
3-2
a
0
−g
t
v
Eine einfache Anwendung dieser Gleichungen ergibt sich
bei dem senkrechten Wurf nach oben und dem freien Fall,
siehe Abbildung links. In beiden Fällen gilt a = −g, wobei
die Erdbeschleunigung mit ca. 9,8 m s−2 einzusetzen ist.
Beim Wurf nach oben kann man in G (3.6) davon
ausgehen, dass die Geschwindigkeit zur Steigzeit t(smax)
null ist, wobei smax die maximale Steighöhe bezeichnet.
Damit ergibt sich aus G (3.6) die Beziehung
v0
t(smax) = v0/g.
t
0
(3.08)
Beginnt man den Wurf nach oben von der Position s = s0
aus, ergibt sich für die maximale Steighöhe aus G (3.07),
a = −g und t(smax) = v0/g die Gleichung
s
smax
smax = s0
s0
t
tsteig
t Wurf und freierFall =
2
v
0
+
.
(3.09)
2g
G (3.08) und G (3.09) beschreiben den Wurf nach oben in
der Zeit 0 < t < tsteig. Beim Wurf nach oben mit der
Anfangsgeschwindigkeit v0 von der Position s = s0 aus und
einem anschließenden freien Fall bis zur Position s = 0 < s0
(die Höhe s = 0 liegt also unterhalb der Höhe, in der der
Wurf beginnt) ergeben sich folgende Gleichungen für Zeit
beziehungsweise Geschwindigkeit
v 0 + v 02 + 2 g s0
g
,
(3.10)
v Wurf und freierFall = − v 02 + 2 g s0 .
(3.11)
Setzen wir s0 = h und v0 = 0 ergeben sich aus den Gleichungen (3.10) und (3.11) die
Spezialfälle des freien Falls aus der Höhe h:
tfreierFall =
2h
,
g
v freierFall = −
2g h .
(3.12)
(3.13)
Der "freie Fall" ist in obiger Abbildung gestrichelt dargestellt.
Grundlagen der Physik für Bauingenieurwesen, © D. Freude
Version vom April 2004
3-3
3.2
Zweidimensionale Bewegung
y
v0
v0sinα
Mehrdimensionale Betrachtungen sind für alle
Dimensionen getrennt zu führen. Ein zweidimensionales Beispiel ist der schiefe Wurf nach oben.
α
g
Mit den Größen aus der rechten Abbildung gilt
v0cosα
x
vx = v0cosα,
vy = v0sinα − gt
(3.14)
(3.15)
x = v0cosα × t,
y = v0sinα × t − gt2/2
(3.16)
(3.17)
und
G (3.16) kann man in t = x/(v0cosα) umstellen und in G (3.17) einsetzen. Dadurch erhält man
die Bahnkurve, die die Zeit nicht mehr explizit enthält:
y = x tan α − x 2
2v
2
0
g
cos 2 α
(3.18)
G (3.18) stellt die Wurfparabel beim schrägen Wurf nach oben dar. Diese Parabel sollte nicht
mit der Parabel in der Zeitabhängigkeit des geraden Wurfs nach oben im Kapitel 3.1
verwechselt werden.
z
3.3
Dreidimensionale Bewegung
r(t)
Eine Bahnkurve (gestrichelte Linie in Abbildung
rechts) im Raum wird durch zeitabhängige
Ortsvektoren r(x,y,z) beschrieben, wobei x, y und z die
zeitabhängigen Ortskoordinaten sind. Die mit x, y und
z in der linken Abbildung bezeichneten Pfeile
bezeichnen die Richtung der Basisvektoren ex, ey und
ez des kartesischen Koordinatensystems.
Aus G (3.01) wird im Raum
∆r
v(t)
r(t + ∆t)
v(t + ∆t)
y
x
v m = r (t + ∆t ) − r (t ) = ∆r
(t + ∆t ) − t
∆t
(3.19)
und aus G (3.02) wird
⎛ x& ⎞
⎜ ⎟
∆r dr
(3.20)
=
= r& = ⎜ y& ⎟ .
v = ∆lim
t →0 ∆t
dt
⎜ z& ⎟
⎝ ⎠
Die Abbildung zeigt, dass der Vektor der Momentangeschwindigkeit stets tangential zur
Bahnkurve ist. Die Bahntangente ergibt sich aus der Verlängerung von dr. Der Einheitsvektor
(Betrag eins) etan hat die Richtung der Momentangeschwindigkeit. Die zeitliche Änderung der
Geschwindigkeit erfolgt in Richtung des Normal-Einheitsvektors enorm. Dieser steht senkrecht
auf etan und zeigt in die Richtung des Mittelpunktes eines Kreises (mit Radius R), mit dessen
Bogenstück die Raumkurve in der Umgebung des momentanen Punktes am besten angepasst
werden kann.
Grundlagen der Physik für Bauingenieurwesen, © D. Freude
Version vom April 2004
3-4
Aus
v = v etan
(3.21)
ergibt sich analog zu G (3.03)
∆v dv d(v e tan ) dv
a = lim
=
=
=
e tan
∆t →0 ∆t
dt
dt
dt
+
v d(e tan ) = a tan + a norm ,
dt
(3.22)
wobei in G (3.22) die Produktenregel der Differentiation angewendet wurde. Aus G (3.22) ist
zu entnehmen, dass der Betrag der Tangentialkomponente der Beschleunigung der zeitlichen
Ableitung des Betrages der Geschwindigkeit entspricht:
dv
a tan =
e tan ,
(3.23)
dt
Da außerdem
de tan v
= e norm
(3.24)
dt
R
gilt, ist die Normalkomponente der Beschleunigung
a norm =
3.4
v2 e
R
norm
.
(3.25)
Drehbewegung
Eine Kreisbewegung kann als beschleunigte Bewegung betrachtet
werden, bei der die Normalkomponente der Beschleunigung stets
zum Kreismittelpunkt gerichtet ist. Für diese
Zentripedalbeschleunigung gilt also
ω
v
a zp =
r
y
v
r
ϕ
x
v2 e
(3.26)
normal
r
Drehbewegung kann durch einen Rotationsvektor ω im Raum
beschrieben. Der Vektor hat den Betrag ω = dϕ/dt und steht
senkrecht auf der Ebene, in der die Drehung stattfindet. Für die
Umfangsgeschwindigkeit v ist
v = ω × r.
(3.27)
Für den Spezialfall einer gleichförmigen Drehung in der x-yEbene zeigt der Rotationsvektor in die z-Richtung. Der bei einer
Rotation um den Winkel ϕ zurückgelegte Weg ist rϕ, wobei der
Winkel ϕ im Bogenmaß (ein rechter Winkel entspricht π/2)
anzugeben ist. Die Frequenz (ν oder f) bzw. Drehzahl (n) einer
Drehung entspricht der reziproken Periodendauer T einer
Umdrehung, und die Kreisfrequenz ω ist das 2π-fache:
2π
.
(3.28)
Τ
Für Zentripedalbeschleunigung azp, Tangentialbeschleunigung atan und Winkelbeschleunigung
α gelten (azp und atan sind lateinische Buchstaben, α ist griechischer Buchstabe)
azp = ω × v = −ω2 r,
atan = α × r ,
(3.29)
2
dω d ϕ
= 2 .
(3.30)
α=
dt
dt
ω = 2π ν =
Grundlagen der Physik für Bauingenieurwesen, © D. Freude
Version vom April 2004