Statische Optimierung unter Ungleichungsrestriktionen (Kuhn

Kapitel 3
Statische Optimierung unter
Ungleichungsrestriktionen
(Kuhn-Tucker)
3.1
Einleitung/Ziel/Bedeutung/Übersicht
• In ökonomischen Anwendungen treten die Restriktionen häufig als Ungleichungen (statt
als Gleichungen) auf.
• Die Lösungen solcher Probleme tendieren dazu, auf dem Rand (genauer gesagt: in einer
‘Ecke’) der zulässigen Menge zu liegen, wo ein Teil der Restriktionen als Gleichungen, der
Rest als echte Ungleichungen erfüllt ist.
• Aus dieser Perspektive ist die Behandlung solcher Probleme deswegen schwieriger, weil
man nicht von vorneherein weiß, welche Restriktionen bindend (als Gleichung erfüllt) sind
und welche nicht (Die Frage ist grob gesagt: Für welche Teilmenge der Restriktionen muss
man Lagrange-Multiplikatoren vorsehen, und für welchen Teil befindet man sich in der
Situation einer unrestringierten Optimierung?)
• Die hier behandelte Vorgehensweise läuft, wenn man sie systematisch einsetzt, auf eine
Reduktion auf viele gleichungsrestringierte Probleme hinaus: Ein ‘Teilproblem’
besteht aus einem Problem, wo ein Teil der Restriktionen als Gleichungen erfüllt sind.
Dieses kann mit dem Lagrange-Formalismus behandelt werden, wobei die restlichen Restriktionen zunächst ignoriert werden. Erfüllt eine Lösung dieses Lagrange-Teilproblems
die restlichen Restriktionen, so hat man einen Lösungskandidaten gefunden.
• Die bindenden Restriktionen als Gleichungen zusammen mit der Abwesenheit (dem Verschwinden) der Lagrange-Multiplikatoren nicht-bindender Restriktionen wird durch komplementäre Schlupfbedingungen beschrieben. Je nachdem, ob maximiert oder minimiert werden soll, müssen auch die Lagrange-Multiplikatoren zu den bindenden Restriktionen eine (schwache) Vorzeichenbed. erfüllen. Der Übersichtlichkeit halber unterstellen
wir eine Maximierungsaufgabe (mit nach außen gerichteten Restriktionsgradienten).
• Das Konglomerat aus Lagrange-Bedingungen und komplementären Schlupfbedingungen
nennen wir die Kuhn-Tucker-Bedingungen. Sie liefern hier die notwendige Bedingung
für die Lösung.
21
22
Statische Optimierung – Kuhn-Tucker
3.2
Definition des Standard-Problems
• Standard-Form des Problems unter Ungleichungs-Restriktionen:
⎧
⎪
⎨ g1 (x1 , . . . xn ) ≤ c1
..
max f (x1 , . . . , xn ) u. d. Nbdg.
.
⎪
⎩
gm (x1 , . . . xn ) ≤ cm
(1)
• D.h. n Variablen, Zielfkt f ist zu maximieren, m Ungleichungsrestriktionen gj ≤ cj (nicht:
gj ≥ cj , nicht: Zielfkt ist zu minimieren)
• Die Menge {x ∈ Rn | gj (x) ≤ cj ∀ j = 1, . . . , m} heißt die zulässige Menge (engl. feasible
set, admissible set), manchmal auch die Opportunitätsmenge.
• Geometrisch: Die durch eine Restriktion gj ≤ cj definierte Menge besteht aus allen Punkten, die ‘auf einer Seite’ der zum Niveau cj gehörenden Isoquante von gj liegen (einschließlich der Isoquante gj = cj selbst; die ‘Seite’ ist die dem Gradienten ∇gj abgewandte Seite).
Die zulässige Menge ist die Schnittmenge all dieser Mengen.
• Zum Beispiel (hier n = 2, m = 2): g1 (x, y) := x2 + y 2 ≤ 1, g2 (x, y) := −y ≤ 0: die zulässige
Menge ist ein Halbkreis, und zwar der Einheitskreis oberhalb der x-Achse.
• Wenn gj eine lineare Funktion in x1 , . . . , xn ist, dann ist die Menge {gj ≤ cj } ein ‘Halbraum’ (ein ‘halber linearer Raum’), der durch die ‘Hyperebene’1 {gj = cj } vom komplementären Halbraum getrennt ist. Sind alle gj linear, dann besteht die zulässige Menge aus
einem Polyeder (Vieleck). Ist auch noch f linear, dann befindet man sich im Bereich der
linearen Optimierung (mit eigenen, sehr effizienten Lösungstechniken, z.B. Simplexverfahren, das sich aber nicht ohne weiteres auf die nicht-lineare Situation übertragen lässt).
• Bedingungen, die Konvexität der zulässigen Menge sicherstellen: Bekannter Satz:
Ist die Funktion gj konvex, so ist jede Menge {gj ≤ cj } konvex (bei konkaven Funktionen
gj sind dagegen die Mengen {gj ≥ cj } konvex). Da der Schnitt konvexer Mengen eine konvexe Menge ergibt, ist die zulässige Menge konvex, wenn alle gj konvexe Funktionen sind.
Ein wichtiger Spezialfall des Standard-Problems liegt vor bei einer (zu maximierenden)
konkaven Ziefunktion f mit konvexen Restriktionen gj ≤ cj .
• Bei (‘nicht-redundanten’) Gleichungsrestriktionen ist nur der Fall m ≤ n relevant (sonst
ist die zulässige Menge leer). Bei Ungleichungsrestrikionen kann jedoch der Fall m > n
durchaus Sinn machen, z.B. erhält man in obigem Beispiel mit g3 (x, y) := −x ≤ 0 einen
Viertelkreis als zulässige Menge.
• Transformation in Standard-Form:
– Minimierungsaufgabe in Standard-Form bringen durch Übergang zu −f ;
– Ungleichungsrestriktionen der Form hj ≥ bj durch Multiplikation mit −1 umschreiben
in −hj ≤ −bj (d.h. Übergang zu gj = −hj , cj = −bj );
– ‘Einschlussrestriktionen’ wie 0 ≤ xj ≤ cj in Standardform bringen durch Verdoppelung der Restriktionen: −xj ≤ 0 und xj ≤ cj .
1
eine Hyperebene ist ein n − 1-dimensionales lineares Gebilde im Rn : Gerade in R2 , Ebene in R3 usw.
c K.H. Schild, Abt. Statistik, Fb. Wiwi, Uni Marburg
3.3
23
Kuhn-Tucker-Bedingungen
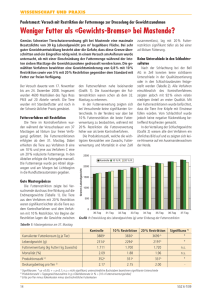
• Wir nennen eine Ungleichungsrestriktion gj (x) ≤ cj bindend (oder aktiv) im Punkt x,
wenn die Restriktion als Gleichung erfüllt ist, d.h. wenn gj (x) = cj . In der folgenden
Skizze bindet die Restriktion g1 (x, y) ≤ c1 im Punkt (x∗ , y ∗ ), die Restriktion g2 (x, y) ≤ c2
dagegen nicht. Dieser Punkt ist die Lösung des Problems max f (x, y) unter den beiden Ungleichungsrestriktionen. Er zeichnet sich dadurch aus, dass in ihm der Gradient der Zielfkt,
∇f (x∗ , y ∗ ), gleichgerichtet ist zum Gradienten der bindenden Restriktion, ∇g1 (x∗ , y ∗ ):
yŧc 2
g 1 Ŧ x , yŧc 1
• Die Skizze legt nahe: Damit ein Punkt x∗ ein lokales Extremum des restringierten Problems
darstellt, muss der Gradient der Zielfunktion eine Linearkombination der Gradienten der
Restriktionen in x∗ sein (wie bei Lagrange), allerdings nur der bindenden:
∇f (x∗ ) = λ1 ∇g 1 (x∗ ) + . . . + λm ∇g m (x∗ ), λj = 0 falls Restriktion j nicht bindet
Damit es sich um ein Maximum handelt, muss der Gradient der Zielfunktion ‘gleichlaufend’ mit den (bindenden) Restriktionsgradienten sein, d.h. λj ≥ 0 für alle j.
Man sollte also nach Punkten x∗ suchen, wo sich der Gradient der Zielfunktion als
Linearkombination der Gradienten der bindenden Restriktionen mit nichtnegativen Linearkoeffizienten λj darstellen lässt:
m
λj ≥ 0 und
λj ∇gj (x∗ ), wobei
∇f (x∗ ) =
λj = 0, falls Restr. j nicht bindet
j=1
• Unter den Kuhn-Tucker-Bedingungen verstehen wir diese Bedingungen zusammen mit der
Forderung, dass die Restriktionen erfüllt sind.
Definition 3.1 (Kuhn-Tucker-Bedingungen) Wir nennen einen Punkt x∗ einen
Kuhn-Tucker-Punkt des Problems (1), wenn er die folgenden Bedingungen erfüllt:
KT1: Für i = 1, . . . , n :
KT2: Für j = 1, . . . , m :
KT3: Für j = 1, . . . , m :
∂f
∗
∂xi (x )
∂gm
∗
∗
1
− λ1 ∂g
∂xi (x ) − . . . − λm ∂xi (x ) = 0
λj ≥ 0,
wobei λj = 0 ist, falls gj (x∗ ) < cj
gj (x∗ ) ≤ cj , wobei gj (x∗ ) = cj ist, falls λj > 0
Anmerkung: Der Zusatz in KT3 ist redundant, da er nur die Kontraposition der Forderung in KT2, Wenn die Restriktion nicht bindet (gj (x∗ ) < cj ), ist λj = 0“, darstellt; er
”
wurde aus Symmetriegründen hinzugefügt.
24
Statische Optimierung – Kuhn-Tucker
• Die Forderungen KT2 und KT3 lassen sich gut merken, wenn man sie – äquivalent – in
Form einer komplementären Schlupfbedingung zwischen λj und gj (x∗ )−cj ausdrückt:
KT2 ∧ KT3 ⇐⇒ λj ≥ 0, gj (x∗ ) − cj ≤ 0, λj · gj (x∗ ) − cj = 0
Wenn gj (x∗ ) − cj < 0 ist (Restriktion bindet nicht), dann muss λj = 0 sein.
Wenn λj > 0 ist, dann ist notwendigerweise gj (x∗ ) − cj = 0 (Restriktion bindet).
Strenggenommen kann man aber nicht von λj = 0 auf gj (x∗ )−cj < 0 oder von gj (x∗ )−cj =
0 auf λj > 0 schließen (obwohl dies im Normalfall gilt, d.h. normalerweise ist die Komplementarität exklusiv). In einem Kuhn-Tucker-Punkt ist zwar immer wenigstens eines von
beiden = 0, λj oder gj (x∗ ) − cj , es kann aber theoretisch auch beides gleichzeitig = 0 sein.
Mit Vektoren lassen sich die komplement. Schlupfbedingungen folgendermaßen schreiben:
λ g(x∗ ) − c = 0
λ ≥ 0, g(x∗ ) − c ≤ 0,
Von den darin involvierten 2m Ungleichungen sind immer (mindestens) m als Gleichungen
erfüllt. Zusammen mit den n Lagr.-Bedingungen aus KT1 ist die Zahl der Gleichungen
also gleich n + m. Dies entspricht gerade der Zahl der Unbekannten in (x, λ).
• Die Implikation x∗ (lokales) Maximum von (1) ⇒ x∗ Kuhn-Tucker-Punkt von (1)“ gilt i.a.
”
leider nur unter einer zusätzlichen Regularitätsbedingung an die bindenden Restriktionen
im Punkt x∗ : Die Gradienten ∇gj (x∗ ) der in x∗ bindenden Restriktionen müssen linear
unabhängig sein. Diese Bedingung (an x∗ ) nennt man die Qualifikationsbedingung.
Satz 3.2 (Kuhn-Tucker als notwendige Bedingung)
Der Punkt x∗ sei eine Lösung des Problems (1), in der die Qualifikationsbedingung erfüllt
ist. Dann erfüllt x∗ die Kuhn-Tucker-Bedingungen.
Dieser Satz würde folgendes Vorgehen nahelegen: Man ermittelt alle Punkte, die die KuhnTucker-Bedingungen erfüllen, sowie alle Punkte mit verletzter Qualifikationsbedingung.
Dies sind die Lösungskandidaten: Sofern das Problem überhaupt eine Lösung hat, weiß
man, dass es einer dieser Punkte ist. Im Normalfall spielt die Qualifikationsbedingung
aber keine Rolle (d.h. sie wird in den Anwendungen oft einfach ignoriert.)
• Neben der Qualifik.Bed. muss im vorhergehenden Satz sichergestellt sein, dass überhaupt
eine Lösung existiert. Diese Annahmen entfallen unter (geeigneten) Konvexitätsannahmen:
Satz 3.3 (KT als hinreichende Bedingung unter Konvexität/Konkavität)
Wenn im Problem (1) die Lagrange-Funktion L(x) := f (x) − λ1 g1 (x) − . . . − λm gm (x)
als Funktion von x bei festgehaltenen λj ≥ 0 konkav ist, so gilt: Wenn ein Punkt x∗ die
Kuhn-Tucker-Bedingungen erfüllt, so stellt er ein globales Max. des Problems (1) dar.
Man beachte, dass die Lagrange-Funktion hier mit −λj“ gebildet wird. Die Satz”
Vorauss. sind dann erfüllt, wenn die Zielfunktion f konkav und alle Restriktionsfunktionen gj konvex sind. Tatsächlich gilt sogar ein etwas stärkerer Satz: Die Konkavität von L in x wird nur bei den zum Kuhn-Tucker-Punkt x∗ gehörigen λ∗j ≥ 0 benötigt.
3.4
Mathematische Beispiele
Bei den folgenden Beispielaufgaben ist das primäre Ziel, sämtliche Kuhn-Tucker-Punkte – als potentielle Lösungen des Problems – zu ermitteln. Um zu einem systematischen Vorgehen zu gelangen, wird per Fallunterscheidung durch alle Kombinationen von bindenden/nichtbindenden Restriktionen iteriert. (Alternativ könnte man die Fallunterscheidung auch auf
den Kombinationen von verschwindenden/positiven λj basieren.) Die Systematik des Vorgehens
hat einen hohen Preis: Der Aufwand steigt wie 2m , d.h. exponentiell mit der Zahl der Restrikt.nen.
c K.H. Schild, Abt. Statistik, Fb. Wiwi, Uni Marburg
25
Beim (auf Restriktionen“ beruhenden) systematischen Vorgehen betrachtet man in jedem der
”
Fälle eine gegebene Kombination von bindenden/nicht-bindenden Restriktionen; dort gilt:
• Die Lagrange-Multiplikatoren der nicht-bindenden Restriktionen verschwinden (sind Null)
• Es bleibt ein Lagrange-System von Gleichungen übrig mit gleich vielen Gleichungen
(Lagrange-Gln. + bindende Restriktionen) wie Unbekannten (normale Variablen xi + verbleibende Lagrange-Multikplikatoren λj der bindenden Restriktionen).
• Dieses Gleichungssystem kann man zunächst lösen und dann überprüfen, ob die Lösungen
die geforderten Ungleichungen (λj ≥ 0 + nicht-bindende Restriktionen) erfüllen.
Beispiel 1: Minimierung von x2 + y 2 unter den Bedingungen x ≥ 2, y ≥ 3 .
0. Problem in Normalform bringen
max f (x, y) := −x2 − y 2 ,
g1 (x, y) := −x ≤ −2,
g2 (x, y) := −y ≤ −3
1. Kuhn-Tucker Bedingungen notieren
a) Lagrange-Funktion (samt Ableitungen nach x, y):
L(x, y) = −x2 − y 2 − λ1 (−x + 2) − λ2 (−y + 3) = −x2 − y 2 + λ1 x + λ2 y + ...
Lx (x, y) = −2x + λ1
Ly (x, y) = −2y + λ2
i.
b) KT-Bedingungen:
ii.
−2x + λ1 = 0
−2y + λ2 = 0
iii. λ1 ≥ 0,
x ≥ 2,
λ1 · (x − 2) = 0
iv. λ2 ≥ 0,
y ≥ 3,
λ2 · (y − 3) = 0
2. Systematisch durch die Kombinationen bindender/nicht-bindender Restriktionen gehen
2.a Beide Restriktionen binden
(Sofort: x = 2, y = 3)
[Prinzipiell: 4 Gln. in 4 Unbekannten (x, y, λ1 , λ2 ), außerdem 2 Ungln. (λ1 ≥ 0, λ2 ≥ 0).]
Die beiden Restriktionen führen auf x = 2, y = 3.
Einsetzen in i. bzw. ii. ergibt λ1 = 4, λ2 = 6.
Da λ1 ≥ 0 und λ2 ≥ 0, liefert dieser Fall den KT-Punkt (x = 2, y = 3, λ1 = 4, λ2 = 6).
2.b Restr. 1 bindet, Restr. 2 nicht.
(Sofort: x = 2, λ2 = 0)
[Prinzipiell: 3 Gln. in 3 Unbekannten (x, y, λ1 ), außerdem 2 Ungln. (y ≥ 3, λ1 ≥ 0).]
Nach iv. ist λ2 = 0, was in ii. auf y = 0 führt. ← hier könnte man schon abbrechen!
Restr. 1 führt auf x = 2, was in i. auf λ1 = 4 führt.
Lösung der Gln. ist also (x = 2, y = 0, λ1 = 4, λ2 = 0). Da y < 3: Kein KT-Punkt.
2.c Restr. 2 bindet, Restr. 1 nicht
(Sofort: y = 3, λ1 = 0)
[Prinzipiell: 3 Gln. in 3 Unbekannten (x, y, λ2 ), außerdem 2 Ungln. (x ≥ 2, λ2 ≥ 0).]
Nach iii. ist λ1 = 0, was in i. auf x = 0 führt. ← hier könnte man schon abbrechen!
Restr. 2 führt auf y = 2, was in i. auf λ2 = 6 führt.
Lösung der Gln. ist also (x = 0, y = 3, λ1 = 0, λ2 = 6). Da x < 2: Kein KT-Punkt.
2.d Keine Restr. bindet.
(Sofort: λ1 = 0, λ2 = 0)
[Prinzipiell: 2 Gln. in 2 Unbekannten (x, y), außerdem 2 Ungln. (x ≥ 2, y ≥ 3).]
Nach iii., iv. ist λ1 = 0, λ2 = 0, und das in i., ii. eingesetzt, ergibt x = 0, y = 0
Lösung der Gln. ist also (x = 0, y = 0, λ1 = 0, λ2 = 0). Kein KT-Punkt, da x = 0 ≥ 2.
3. Diskussion (ob einer – und falls ja, welcher – der KT-Punkte das Problem löst).
Zielfkt konkav, Restriktionen linear ⇒ Die KT-Bedingungen sind auch hinreichend (ohne
Qualif.Bed.). Damit ist der (einzige) KT-Punkt aus Fall 2.a die Lösung des Problems.
26
Statische Optimierung – Kuhn-Tucker
Beispiel 2: Maximierung von y − x auf dem Halbkreis {(x, y) : x2 + y 2 ≤ 1, y ≥ 0} .
Normalform des Problems:
g1 (x, y) := x2 + y 2 ≤ 1
max f (x, y) := y − x u. d. Nbdg.
g2 (x, y) := −y ≤ 0
Lagrange-Funktion und ihre Ableitungen:
L(x, y) = y − x − λ1 (x2 + y 2 ) + λ2 y
Lx (x, y) = −1 − 2λ1 x
Ly (x, y) = 1 − 2λ1 y + λ2
Kuhn-Tucker-Bedingungen:
i. −1 − 2λ1 x = 0
ii.
1 − 2λ1 y + λ2 = 0
iii. λ1 ≥ 0,
x2 + y 2 ≤ 1,
iv. λ2 ≥ 0,
y ≥ 0,
λ1 · (x2 + y 2 − 1) = 0
λ2 · y = 0
Fall 1: Beide Restriktionen binden: x2 + y 2 = 1, y = 0
Wenn y = 0 in ii., dann ist λ2 = −1 < 0. Der Fall liefert also keinen Kuhn-Tucker-Punkt.
Fall 2: Restr. 1 bindet, Restr. 2 nicht: x2 + y 2 = 1, y > 0 (⇒ λ2 = 0)
Mit λ2 = 0 bleiben (neben den Ungln. y ≥ 0, λ1 ≥ 0) 3 Gleichungen in 3 Unbekannten
−1 − 2λ1 x = 0
1 − 2λ1 y = 0
x2 + y 2 = 1
Indem wir i. und ii. nach λ1 auflösen und die entstehenden Ausdrücke gleichsetzen, ergibt
sich λ1 = −1/2x = 1/2y, also y = −x (x = 0 führt auf Widerspruch −1 = 0, y = 0
auf 1 = 0). Ersetzung von y 2 durch x2 in x2 + y 2 = 1 liefert schließlich (wenn wir y > 0
berücksichtigen) einen (einzigen) KT-Punkt: x = − √12 , y =
√1 ,
2
λ1 =
√
2
2
=
√1 ,
2
λ2 = 0
Dieser Punkt erfüllt auch die nicht-bindenden Restriktionen, hier y ≥ 0, und die λj zu den
bindendend Restriktionen, hier nur λ1 , sind ≥ 0.
Fall 3: Restr. 2 bindet, Restr. 1 nicht: x2 + y 2 < 1, y = 0 (⇒ λ1 = 0)
Mit λ1 = 0 wird ii. zu λ2 = −1 ⇒ kein Kuhn-Tucker-Punkt
Fall 4: Keine der Restriktionen bindet: x2 + y 2 < 1, y > 0 (⇒ λ1 = λ2 = 0)
Mit λ1 = λ2 = 0 wird i. zu 1 = 0. Also kein Kuhn-Tucker-Punkt.
Der ermittelte Kuhn-Tucker-Punkt aus Fall 2 realisiert das globale Max. der Zielfunktion, da
die Zielfkt. linear (und damit konkav) ist und die Restriktionsfunktionen konvex sind.
Anmerkung: Bei diesem Beispiel ergibt sich sehr schnell, dass man ohnehin nur im Fall erste
”
Restriktion bindet, zweite Restrikt. bindet nicht“ Kuhn-Tucker-Punkte bekommen kann:
• Aus i. folgt sofort: λ1 = 0. Die kompl. Schlupfbed. λ1 · (x2 + y 2 − 1) = 0 liefert dann
x2 + y 2 = 1, d.h. die erste Restriktion bindet in den Kuhn-Tucker-Punkten.
• Aus ii. folgt λ2 = −1 + 2λ1 y, wobei wir schon λ1 > 0 wissen. Wäre y = 0, so wäre λ2 = −1
negativ, im Widerspruch zu λ2 ≥ 0. Also ist y > 0. Die zweite Restriktion bindet also
nicht in den Kuhn-Tucker-Punkten.
Man hätte also auf die Fallunterscheidung verzichten und direkt in die Analyse von Fall 2
einsteigen können.
c K.H. Schild, Abt. Statistik, Fb. Wiwi, Uni Marburg
27
Beispiel 3: Minimierung von y − x auf dem Halbkreis {(x, y) : x2 + y 2 ≤ 1, y ≥ 0} .
g1 (x, y) := x2 + y 2 ≤ 1
Normalform: max f (x, y) := x − y u. d. Nbdg.
g2 (x, y) := −y ≤ 0
L(x, y) = x − y − λ1 (x2 + y 2 ) + λ2 y
Lx (x, y) = 1 − 2λ1 x
Lagrange-Funktion samt Ableitungen:
Ly (x, y) = −1 − 2λ1 y + λ2
i. 1 − 2λ1 x = 0
ii. −1 − 2λ1 y + λ2 = 0
Kuhn-Tucker-Bedingungen:
iii. λ1 ≥ 0, x2 + y 2 ≤ 1, λ1 · (x2 + y 2 − 1) = 0
iv. λ2 ≥ 0, y ≥ 0, λ2 · y = 0
Anstelle des systematischen Vorgehens ermitteln wir, in welchem Fall die Bindungsrestriktionen
überhaupt zu Kuhn-Tucker-Punkten führen können:
• Aus i. folgt sofort: λ1 = 0. Die kompl. Schlupfbed. (λ1 · (x2 + y 2 − 1) = 0) liefert dann
x2 + y 2 = 1, d.h. die erste Restriktion bindet in den Kuhn-Tucker-Punkten.
• Aus ii. folgt λ2 = 1 + 2λ1 y. Da λ1 ≥ 0 und y ≥ 0, folgt λ2 > 0. Mit der kompl. Schlupfbed.
iv. ergibt sich y = 0.
D.h. hier binden beide Restriktionen. Die Kuhn-Tucker-Punkte müssen das System der Restriktionsgleichungen x2 + y 2 = 1, y = 0 lösen, was auf x = ±1, y = 0 führt. Den Fall x = −1
können wir ausschließen, da sonst λ1 = 1/2x < 0. Es verbleibt als einziger Kuhn-Tucker-Punkt
(x, y) = (1, 0) mit λ1 = λ2 = 0. Da wir uns wieder im Szenario Zielfkt. konkav, Restriktionen
”
konvex“ befinden, realisiert er das globale Max. der Zielfunktion.
max f (x, y) := x2 + y u. d. Nbdg. x2 + y 2 ≤ 1, y ≥ 0
g1 (x, y) := x2 + y 2 ≤ 1
2
Normalform:
max f (x, y) := x + y u. d. Nbdg.
g2 (x, y) := −y ≤ 0
Lagrange-Funktion samt Ableitungen nach x, y:
L(x, y) = x2 + y − λ1 (x2 + y 2 ) + λ2 y
Beispiel 4:
Lx (x, y) = 2x − 2λ1 x
Ly (x, y) = 1 − 2λ1 y + λ2
Kuhn-Tucker-Bedingungen:
i. 2x − 2λ1 x = 0
ii.
1 − 2λ1 y + λ2 = 0
iii. λ1 ≥ 0,
x2 + y 2 ≤ 1,
iv. λ2 ≥ 0,
y ≥ 0,
x2
λ1 · (x2 + y 2 − 1) = 0
λ2 · y = 0
y2
Fall 1: Beide Restriktionen binden:
+ = 1, y = 0
Wenn y = 0 in ii., dann ist λ2 = −1 < 0. Der Fall liefert daher keinen KT-Punkt.
Fall 2: Restr. 1 bindet, Restr. 2 nicht: x2 + y 2 = 1, y > 0 (⇒ λ2 = 0)
Mit λ2 = 0 bleiben (neben den Ungln. y ≥ 0, λ1 ≥ 0) 3 Gleichungen in 3 Unbekannten
i. 2x − 2λ1 x = 0 ( ⇐⇒ 2x (1 − λ1 ) = 0 ⇐⇒ (x = 0) ∨ (λ1 = 1))
ii.
1 − 2λ1 y = 0
iii. x2 + y 2 = 1
√
Im Fall λ1 = 1 haben die beiden letzten Gln. die Lösung y = 12 , x2 = 34 , d.h. x = ± 23 .
Im Fall x = 0 ergibt sich aus der letzten Gl. y = 1 (und aus der vorletzten λ1 = 12 ).
√
√
Fazit: Dieser Fall liefert drei Kuhn-Tucker-Punkte (x, y) ∈ {( 23 , 12 ), (− 23 , 12 ), (0, 1)}.
(Jeder dieser Punkte erfüllt auch die nicht-bindenden Restriktionen, hier y ≥ 0, und die
λj zu den bindendend Restriktionen, hier nur λ1 , sind ≥ 0).
28
Statische Optimierung – Kuhn-Tucker
Fall 3: Restr. 2 bindet, Restr. 1 nicht: x2 + y 2 < 1, y = 0 (⇒ λ1 = 0)
Mit λ1 = 0 wird ii. zu λ2 = −1 ⇒ kein Kuhn-Tucker-Punkt
Fall 4: Keine der Restriktionen bindet: x2 + y 2 < 1, y > 0 (⇒ λ1 = λ2 = 0)
Mit λ1 = λ2 = 0 wird ii. zu 1 = 0. Also kein Kuhn-Tucker-Punkt.
Insgesamt gibt es also drei Kuhn-Tucker-Punkte (die alle aus Fall 2 kommen, d.h. auf dem
Rand des Einheitskreises liegen). Die Zielfkt f (x, y) = x2 + y nimmt in ihnen folgende Werte an:
f (±
√
3 1
2 , 2)
=
3
4
+
1
2
=
5
4,
f (0, 1) = 1
Bei diesem Beispiel sind die KT-Bedingungen keine hinreichende Bedingungen für die Lösung, da
wir uns nicht im ‘richtigen’ Konvexitätsszenario befinden. D.h. der zweite Satz greift nicht und
wir sind auf den ersten Satz angewiesen. Strengennommen müssen zu dessen Anwendung auch
noch die Punkte, die die Qualifikationsbed. nicht erfüllen, ermittelt und als Lösungskandidaten
in Betracht gezogen werden. Eine entsprechende, hier nicht vorgeführte Analyse (auf Basis der
gleichen Fallunterscheidung) zeigt, dass es keine Punkte mit Verletzung der Qualifikationsbed.
gibt. Außerdem muss sichergestellt sein, dass das vorliegende Problem überhaupt eine Lösung
hat (da der Satz sich sonst auf die leere Menge bezieht). Ein berühmter Satz aus der Mathematik
(Satz von Weierstraß) besagt, dass eine auf einer kompakten (=beschränkten und abgeschlossenen) Menge stetige Fkt dort ihr Max. annimmt. Da der (abgeschlossene) Halbkreis kompakt
ist, existiert eine Lösung.
√
Fazit: Das Problem hat (genau) die beiden Lösungen (x = ± 23 , y = 12 ).
Beispiel 5: min 4 ln(x2 + 2) + y 2
u.d.NB. y ≥ 2 − x2 , x ≥ 1
g1 (x, y) := −x2 − y ≤ −2
2
2
Normalform: max f (x, y) := −4 ln(x + 2) − y u. d. Nbdg.
g2 (x, y) := −x ≤ −1
Lagrange-Fkt:
2
2
2
L(x, y) = −4 ln(x + 2) − y + λ (x + y − 2) + λ x
1
2
8x
Lx (x, y) = − 2
+ 2λ1 x + λ2
x +2
Ly (x, y) = −2y + λ1
KT-Bedingungen:
8x
+ 2λ1 x + λ2 = 0
+2
−2y + λ1 = 0
← schön einfach: →
i.
−
ii.
x2
2
iii. λ1 ≥ 0,
x + y ≥ 2,
iv. λ2 ≥ 0,
x ≥ 1,
λ1 = 2y
2
λ1 · (x + y − 2) = 0
λ2 · (x − 1) = 0
x2
Fall 1: Beide Restriktionen binden:
+ y = 2, x = 1 Mit x = 1 folgt zunächst y = 2 − x2 =
2 − 1 = 1. Einsetzen in ii. liefert zwar λ1 = 2y = 2 ≥ 0, aber beim Einsetzen in i.:
λ2 = x28x+2 − 2λ1 x = 83 − 2 · 2 = − 43 entsteht λ1 < 0. Der Fall liefert also keinen KT-Punkt.
Fall 2: Restr. 1 bindet, Restr. 2 nicht: x2 + y = 2, x > 1 (⇒ λ2 = 0)
Prinzipiell: 3 Gleichungen (i., ii., NB1) in 3 Unbekannten (x, y, λ1 )
→ lösen, schauen ob verbleibende Ungln. λ1 ≥ 0, NB2 (x ≤ 1) erfüllt sind.
Gleichungen i. u. ii. für λ2 = 0:
i.
ii.
8x
+ 2λ1 x = 0
+2
2y = λ1
−
x2
N B1 y = 2 − x2
Substituiere λ1 = 2y und y = 2 − x2 in i., liefert Gleichung nur noch in x:
c K.H. Schild, Abt. Statistik, Fb. Wiwi, Uni Marburg
−
29
8x
+ 4(2 − x2 ) x = 0 ⇐⇒ x = 0 ∨ 4 (4 − x4 ) = 8
+2
⇐⇒ x = 0 ∨ 4 − x4 = 2
x2
⇐⇒ x = 0 ∨ x4 = 2
√
4
Da x > 1, bleibt nur x = + 2.
√
√
Dann ergibt sich y = 2 − x2 = 2 − 2 > 0 und λ1 = 2y = 4 − 2 2 > 0
√
√
√
Der Fall liefert also den KT-Punkt (x = 4 2, y = 2 − 2, λ1 = 4 − 2 2, λ2 = 0) .
Fall 3: Restr. 2 bindet, Restr. 1 nicht: x2 + y > 2, x = 1 (⇒ λ1 = 0)
Mit x = 1 und λ1 = 0 (⇒ y = 0 aus ii) ist die NB x2 + y > 2 verletzt. Also kein KT-Punkt
Anm: kein Widerspruch aus i.: λ2 =
8x
x2 +2
− 2λ1 x =
8
3
+0=
8
3
≥ 0.
Fall 4: Keine der Restriktionen bindet: x2 + y > 2, x > 1 (⇒ λ1 = λ2 = 0)
Mit λ1 = λ2 = 0 bilden i. und ii. ein 2 × 2- Gl.System in (x, y) (das einer unrestringierten
Optimierung von f )
Hier sehr einfach: ii. ⇒ y = 0 und Einsetzen in i. liefert: − x28x+2 = 0 ⇒ x = 0.
D.h. (0, 0) wäre Lösung des unrestr. Problems. Da x > 1 gefordert: Kein KT-Punkt
√
√
Insgesamt gibt es also nur einen Kuhn-Tucker-Punkt (x = 4 2, y = 2 − 2). Wenn das Problem
ein Lösung hat, kommt nur dieser Punkt in Frage (Qualifikationsbedingung außen vor).
(Da der zulässige Bereich hier keine kompakte Menge ist, ist der Weierstraß-Satz aber nicht anwendbar.
Wir übergehen den Nachweis, dass das Problem überhaupt eine Lösung hat.)
3.5
Übungsaufgaben
Bestimmen Sie für die folgenden Probleme sämtliche KT-Punkte (optional: Lösung diskutieren).
Aufg. KT.1a:
Minimiere f (x, y) = x2 + 2y unter den Nebenbedingungen x2 + y 2 ≤ 4, y ≥ 0
Aufg. KT.1b:
Maximiere f (x, y) = x2 + 2y unter den Nebenbedingungen x2 + y 2 ≤ 4, y ≥ 0
Aufg. KT.2a:
Maximiere f (x, y) = x2 + y u. d. Nebenbed. x2 + y 2 ≤ 2, y ≥ x
Aufg. KT.2b:
Maximiere f (x, y) = x2 + y u. d. Nebenbed. x2 + y 2 ≤ 54 , y ≥ 12 x
Aufg. KT.3a:
Maximiere f (x, y) = x · y u. d. Nebenbed. x2 + y 2 ≤ 2, x + y ≤ 1
Aufg. KT.3b:
Maximiere f (x, y) = x · y + x + y u. d. Nebenbed. x2 + y 2 ≤ 2, x + y ≤ 1
Aufg. KT.4a:
Minimiere f (x, y) = x3 + y 2 − 27x − 4y u. d. Nebenbed. x ≥ 0, y ≥ 0
Aufg. KT.4b:
Maximiere f (x, y) = x3 + y 2 − 27x − 4y u. d. Nebenbed. x ≥ 0, y ≥ 0
Aufg. KT.5a:
min 4 ln(x2 + 2) + y 2
u.d.NB. y ≥ 2 − x2 , x ≥ 1
Aufg. KT.5b:
min 4 ln(x2 + 2) − y 2
u.d.NB. y ≥ 2 − x2 , x ≥ 1
30
Statische Optimierung – Kuhn-Tucker
3.6
Anwendung: Optimierung der Bilanzstruktur einer Bank
(Orientiert sich an Karmann, Mathematik für Wirtschaftswissenschaftler, 5. Aufl, letztendlich
wird ein lineares Optimierungsproblem unterstellt, das man einfacher lösen könnte.)
• Die Bank hat als Passiva
– Eigenkapital
– Einlagen von Kunden mit Laufzeit von einem Monat
– Einlagen von Kunden mit Laufzeit von drei Monaten.
• Als Aktiva vergibt die Bank Kredite, ebenfalls mit Laufzeiten von 1 Monat und 3 Monaten.
Verbleibende Einlagen (wegen nicht-in-Anspruch-genommener Kredite) von der Passivseite
werden auf der Aktiv-Seite kompensiert, indem sie auf ein EZB-Konto gebucht werden.
• Es sei von folgender Anfangsbilanz ausgegangen (alle Angaben in Mrd. Euro):
Aktiva
Kredite (1 Monat)
Kredite (3 Monate)
EZB
A1 = 20.0
A2 = 9.0
ABar = 2.4
Summe
A = 31.4
Passiva
Einlagen (1 Monat)
Einlagen (3 Monate)
Eigenkapital
P1 = 21.0
P2 = 5.8
PEK = 4.6
Summe:
P = 31.4
• Zu Beginn der Planungsperiode erhält die Bank zusätzliche Einlagen
– mit einer Laufzeit von 1 Monat: 2.0
– mit einer Laufzeit von 3 Monaten: 3.5
(neu)
(neu)
D.h. die neuen Passivpositionen sind P1
= 23.0, P2
= 9.3
Das Eigenkapital bleibt unverändert
• Die Bank vergibt neue Kredite im Umfang von x1 bzw. x2 , so dass sich die Aktivpositionen
von A1 zu A1 + x1 und von A2 zu A2 + x2 verändern.
Ziel ist es, die Volumina x1 und x2 (über die von der Bank festzulegenden Zinssätze) so
zu ‘wählen’, dass der Gewinn der Bank aus den neuen Krediten maximal wird.
Dazu wird unterstellt, dass der Bank die ‘Preis-Absatz-Fktnen’ r1 (x1 ) und r2 (x2 ) bekannt
sind, die den Zinssatz ri angeben, bei dem das Volumen xi nachgefragt wird.
→ Preissetzer-Modell: Optimiert wird über x, obwohl eigentlich der Zins r(x) gesetzt wird.
Der Gewinn ist dann G(x1 , x2 ) = r1 (x1 ) · x1 + r2 (x2 ) · x2
• Diese Funktion ist unter folgenden Restriktionen zu maximieren:
1.
2.
3.
4.
x1 + x2 − 5.5
0.08 · (A1 + x1 + A2 + x2 )
A1 + x1 + ABar
A2 + x2
≤
≤
≥
≥
0
PEK
(neu)
P1
(neu)
P2
(Bilanzausgleich, Σ Aktiva = Σ Passiva)
(Grundsatz I)
(Grundsatz II)
(Grundsatz II)
– Grundsatz I:
Die riskanten Aktiva müssen zu mindestens 8% durch Eigenkapital unterlegt sein.
– Grundsatz II: Das Volumen der Aktiva muss mindestens so hoch sein wie das der
Passiva mit gleicher Laufzeit; dies gilt für jede Laufzeit (soll Liquidität sicherstellen).
• Außerdem gelten die Restriktionen x1 ≥ 0, x2 ≥ 0, die wir im Folgenden zunächst ignorieren (womit wir davon ausgehen, dass sie ohnehin erfüllt wären und nicht binden würden).
c K.H. Schild, Abt. Statistik, Fb. Wiwi, Uni Marburg
31
• Lagrange-Funktion
L(x1 , x2 ) = r1 (x1 ) · x1 + r2 (x2 ) · x2
− λ1 · x1 + x2 − 5.5
− λ2 · 0.08 · A1 + x1 + A2 + x2 − PEK
(neu)
− λ 3 · P1
− A1 − x1 − ABar
(neu)
− λ 4 · P2
− A2 − x2
Lx1 (x1 , x2 ) = r1 (x1 ) x1 + r1 (x1 ) − λ1 − 0.08 λ2 + λ3
Lx1 (x1 , x2 ) = r2 (x2 ) x2 + r2 (x2 ) − λ1 − 0.08 λ2
+ λ4
• Kuhn-Tucker-Bedingungen:
i. r1 (x1 ) x1 + r1 (x1 ) − λ1 − 0.08 λ2 + λ3 = 0
ii.
r2 (x2 ) x2 + r2 (x2 ) − λ1 − 0.08 λ2
iii. λ1 ≥ 0,
iv. λ2 ≥ 0,
v.
λ3 ≥ 0,
vi. λ4 ≥ 0,
+ λ4 = 0
x1 + x2 ≤ 5.5, λ1 · (x1 + x2 − 5.5) = 0
A1 + x1 + A2 + x2 − PEK ≥ 0, λ2 · A1 + x1 + A2 + x2 − PEK = 0
(neu)
(neu)
P1
− A1 − x1 − ABar ≥ 0, λ3 · P1
− A1 − x1 − ABar = 0
(neu)
(neu)
P2
− A2 − x2 ≥ 0, λ3 · P2
− A2 − x2 = 0
• Unter der (nicht unrealistischen) Annahme, dass die Funktionen ri (x) monoton fallend
und konkav sind, ist die Ziel/Gewinnfkt. G(x1 , x2 ) konkav. Da die Restriktionen linear
sind, sind die KT-Bedingungen dann notwendig und hinr. für ein (globales) Maximum.
• Entsprechend dem obigen ‘systematischen Vorgehen’ wären nun alle 2m = 16 Kombinationen von bindenden und nicht-bindenden Restriktionen durchzugehen.
Exemplarisch die KT-Bedingungen, wenn
– Restriktion 1 (Bilanzsummen-Ausgleich) und
– Restriktion 3 (Liquiditäts-Grundsatz II für kurzfristige Kredite)
binden, aber
– Restriktion 2 (mind. 8% EK-Deckung der riskanten Kredite) und
– Restriktion 4 (Liquiditäts-Grundsatz II für langfristige Kredite)
nicht binden.
Dann ist λ2 = λ4 = 0 und wir erhalten folgende vier Gleichungen für x1 , x2 , λ1 , λ3
i.
ii.
r1 (x1 ) x1 + r1 (x1 ) − λ1 + λ3 = 0
r2 (x2 ) x2 + r2 (x2 ) − λ1 = 0
iii. x1 + x2 = 5.5
v.
(neu)
x1 = P1
− A1 − ABar
(Nach Lösung dieses Gl.systems ist zu überprüfen, ob λ1 ≥ 0, λ3 ≥ 0 und auch die beiden
als nicht-bindend angenommenen Restriktionen 2 und 4 erfüllt sind.)
• Wenn wir auch noch r1 (x) = const = 8% und r2 (x) = const = 9% unterstellen (d.h.
Kreditnachfrage ‘springt’ bei ‘Schwellen-Zinssätzen’), wird dies zum linearen Gl.System
i.
−λ1 + λ3 = −0.08
ii.
−λ1 = −0.09
iii. x1 + x2 = 5.5
v.
(neu)
x1 = P1
− A1 − ABar
32
Statische Optimierung – Kuhn-Tucker
mit der Lösung
x∗1 = 0.6,
x∗2 = 4.9,
λ∗1 = 0.09,
λ∗3 = 0.01
Da dieser Punkt auch die Restriktionen 2) und 4) erfüllt und alle λj ≥ 0 sind, ist er ein
KT-Punkt. Er ist der einzige im vorliegenden Beispiel und damit Lösung des Problems.
Da wir letztendlich eine lineare Zielfunktion mit linearen Restriktionen unterstellt haben,
können wir das Problem auch mit einem Simplexverfahren lösen, was viel effizienter als
das Durchprobieren der Restriktionskombinationen ist und auf die angegeb. Lösung führt.
• Das Ergebnis soll noch einmal zusammengestellt werden. Ausgangsbilanz war:
Aktiva
Kredite (1 Monat)
Kredite (3 Monate)
EZB
A1 = 20.0
A2 = 9.0
ABar = 2.4
A = 31.4
Summe
Passiva
Einlagen (1 Monat)
Einlagen (3 Monate)
Eigenkapital
Summe:
P1 = 21.0
P2 = 5.8
PEK = 4.6
P = 31.4
Dann erhielt die Bank 5.5 (Mrd. Euro) an neuen Einlagen, und zwar 2.0 in P1 und 3.5 in P2 .
Das Ergebnis besagt, dass – zur Gewinnmaximierung unter den angegeb. Restriktionen –
diese Positionen wie folgt auf die Aktiva verteilt werden sollten: x1 = 0.6 in A1 und
x2 = 4.9 in A2 . Damit ergibt sich folgende neue Bilanz:
Aktiva
Kredite (1 Monat)
Kredite (3 Monate)
EZB
A1 = 20.6
A2 = 13.9
ABar = 2.4
Summe
A = 36.9
Passiva
Einlagen (1 Monat)
Einlagen (3 Monate)
Eigenkapital
Summe:
P1 = 23.0
P2 = 9.3
PEK = 4.6
P = 36.9
• Wir lassen nun zu, dass die Bank auch Geld bei der EZB einlegt, zum Zins von r3 = 1%,
so dass die Gewinnfunktion zu G(x1 , x2 , x3 ) = r1 ·x1 +r2 ·x2 + r3 ·x3 wird. Diese Funktion
ist nun unter x1 ≥ 0, x2 ≥ 0, x3 ≥ 0 sowie folgenden Restriktionen zu maximieren:
1.
2.
3.
4.
x1 + x2 + x3
0.08 · (A1 + x1 + A2 + x2 )
A1 + x1 + ABar + x3
A2 + x2
≤
≤
≥
≥
5.5
PEK
(neu)
P1
(neu)
P2
(Bilanzausgleich, Σ Aktiva = Σ Passiva)
(Grundsatz I)
(Grundsatz II für kurzfristige Kredite)
(Grundsatz II für langfristige Kredite)
Das Ergebnis (mit Simplexverf) bzgl. x1 und x2 ändert sich nicht gegenüber dem alten
Ergebnis, da x∗3 = 0 gefunden wird (klar, bei der EZB betragen die Zinsen nur bei 1%).
• Als nächstes lassen wir die Restriktion x3 ≥ 0 weg. Ein negatives x3 bedeutet, dass die
Bank sich Geld bei der EZB zum Zins von 1% borgt. Das Ergebnis überrascht etwas
(und erinnert an Blasen-Bildung auf dem Finanzmarkt): x1 = 52.6, x2 = 4.9, x3 = −52
(und der Gewinn verzehnfacht sich etwa). Außerdem bindet jetzt neben der Bilanzsumme
und der kurzfristigen Liquidität auch die EK-Restriktion. Die Bank borgt sich also in
großem Umfang Geld von der EZB zum Zins von 1%, um kurzfristige Kredite, für die
sie 8% bekommt, zu vergeben. Der Umfang dieses Arbitrage-Geschäfts wird durch die
Restriktion der geforderten minimalen EK-Deckung limitiert.
Wird der geforderte Satz für die EK-Deckung von 8% auf 20% erhöht, so liefert die GewinnMaximierung: x1 = 18.1, x2 = 4.9, x3 = −17.5 .
c K.H. Schild, Abt. Statistik, Fb. Wiwi, Uni Marburg
3.7
33
Nicht-Negativitätsbedingungen
In ökonom. Anwendungen hat man meist die Bedingung, dass sämtliche Variablen x1 , . . . , xn
(zwar 0, aber) nicht negativ werden können. Anstatt die Nicht-Negativitäts-Bedingungen xi ≥ 0
den ‘normalen’ Restriktionen gj ≤ cj zuzurechnen, gestehen wir ihnen nun eine Sonderrolle zu
und betrachten das Maximierungsproblem (1) mit insgesamt m + n Restriktionen
⎧
⎪
⎨ g1 (x1 , . . . xn ) ≤ c1
..
, x1 ≥ 0, . . . , xn ≥ 0
max f (x1 , . . . , xn ) u. d. Nbdg.
.
⎪
⎩
gm (x1 , . . . xn ) ≤ cm
Mit den n zusätzlichen Lagrange-Multplikatoren μ1 , . . . , μn lauten die Kuhn-Tucker-Bedingungen:
m
∂gj
∂f
j=1 λj ∂xi + μi = 0 für i = 1, . . . , n
∂xi −
λj · gj (x∗ ) − cj = 0
gj (x∗ ) − cj ≤ 0, λj ≥ 0,
für j = 1, . . . , m
xi ≥ 0, μj ≥ 0,
μi · ( xi − 0 ) = 0
für i = 1, . . . , n
zusammenDa μi ≥ 0 und μi = 0, falls xi > 0, kann die erste und dritte Bedingung
m äquivalent
∂gj
∂f
gefasst werden in Form einer komplementären Schlupfbed. für ∂x
−
λ
und
xi :
j
j=1
∂xi
i
Definition 3.4 (Kuhn-Tucker-Bedingungen bei Nicht-Negativitätsbedingungen)
∂f
m
m
∂gj
∂gj ∂f
j=1 λj ∂xi ≤ 0, xi ≥ 0, xi · ∂xi −
j=1 λj ∂xi = 0 für i = 1, . . . , n
∂xi −
gj (x∗ ) − cj
= 0 für j = 1, . . . , m
gj (x∗ ) − cj ≤ 0, λj ≥ 0, λj ·
In dieser (äquiv.) Formulierung der KT-Bedingungen fällt die Symmetrie oder ‘Dualität’ zwischen den beiden kompl. Schlupfbedingungen auf (worauf wir im nächsten Abschnitt eingehen).
Abgesehen davon hat die symmetrische Form der KT-Bedingungen aber kaum Vorteile bei der
Anwendung unseres ‘systematischen Vorgehens’ auf konkrete Probleme, denn dazu müssen nach
wie vor sämtliche Kombinationen von Bindungen (nun 2m+n Stück) durchgegangen werden.
3.7.1
Anwendung: Gewinnmaximierendes Mehrproduktunternehmen
Die Bedeutung der Kuhn-Tucker-Bedingungen soll anhand eines Unternehmens erläutert werden, das n Produkte in den Mengen x1 , . . . , xn zu (exogen vorgegebenen) Preisen p1 , . . . , pn
absetzen kann, wobei (Produktions-) Kosten in Höhe von K(x1 , . . . , xn ) entstehen. Ziel des Unternehmens ist die Festlegung der Produktionsmengen x = (x1 , . . . , xn ) so, dass der Gewinn
G(x1 , . . . , xn ) = p1 x1 + . . . + pn xn − K(x1 , . . . , xn ) bzw. G(x) = p x − K(x)
maximal wird. Wir unterstellen eine (in jedem xi wachsende und) konvexe Kostenfkt. K(x); die
Zielfunktion G(x) ist dann konkav in x.
Der Interpretation der KT-Bedingungen nähern wir uns schrittweise:
1. Unrestringierte Gewinnmaximierung
Bei einer unrestringierten Optimierung lautet die notwendige Bedingung ∇G = 0, also
∂K
p − ∇K = 0 bzw. pi = ∂x
( Preis = Grenzkosten“). Da wir mit der Konvexität von
i
”
∂K
K wachsende Grenzkosten ∂xi unterstellen, bedeutet dies, dass ein gewinnmaximierendes Unternehmen die Produktionsmenge xi solange erhöhen (bzw. drosseln) wird, wie die
nächste produzierte Einheit weniger (bzw. mehr) Kosten verursacht als der Erlös aus ihrem
Absatz, das ist der Preis pi , einbringt.2 Die Devise Erhöhe die Produktion solange, bis
”
die Grenzkosten des Produkts mit dessen (exogen vorgegebenem) Preis übereinstimmen.“
ist das typische Ergebnis für ein gewinn-maximierendes Unternehmen unter vollständigem
Wettbewerb, wie wir es hier mit den exogen vorgegebenen Preisen pi unterstellen.
2
Dies ist eine vereinfachte Darstellung, da Interaktionseffekte in den Kosten nicht berücksichtigt werden.
34
Statische Optimierung – Kuhn-Tucker
2. Gewinnmaximierung unter den Bedingungen xi ≥ 0 (ohne sonstige Restrikt.en)
Zu erwarten ist hier, dass das UN diejenigen Güter i, deren initiale (bei xi = 0 vorliegenden) Grenzkosten bereits über dem Absatzpreis liegen, überhaupt nicht produzieren wird,
während für die anderen Güter die Prod.menge solange angehoben wird bis die Grenzkosten beim Level des Absatzpreises angekommen sind. 3 Die KT-Bedingungen drücken dies
im Wesentlichen aus. Wenn keine weiteren Restriktionen vorliegen (d.h. m = 0), reduzieren
sie sich auf
xi ≥ 0, xi · (pi − ∂K
pi ≤ ∂K
= 0
xi ,
xi
Dies besagt: Im Gewinnmaximum werden nur solche Güter in positiver Quantität produziert (xi > 0), für die die Grenzkosten dem Preis entsprechen (pi = ∂K
xi ). Liegen die
∂K
Grenzkosten eines Gutes im Optimum strikt über dessen Preis (pi < xi ), wird die Produktion dieses Gutes eingestellt (xi = 0). Liegen die Grenzkosten für ein Gut mit positiver
Produktion xi > 0 unter dessen Preis, befindet man sich nicht im Gewinnmaximum.
3. Gewinnmaximierung unter Nicht-Negativ.-Beding.en u. Ressourcenknappheit
Jetzt wird zusätzlich angenommen, dass das Unternehmen für die Produktion eine Ressource benötigt, die ihm (zwar kostenlos, aber nur) in beschränkter Kapazität c zur Verfügung
steht; zur Produktion einer Einheit des Gutes i werden ai Einheiten der Ressource benötigt.
Wenn z.B. die Ressource die im Unternehmen eingestellten Beschäftigten sind, deren Arbeitskraft in Stunden gemessen wird, dann gibt ai die Zahl der Arbeitsstunden an, die
zur Produktion eines Stücks des i-ten Gutes benötigt werden. Ziel des Unternehmens sei
wieder die Maximierung des Gewinns, diesmal unter Einhaltung der Ressourcenkapazität:
max p x − K(x) u. d. Nbdg. x ≥ 0, a x ≤ c
x
Die Kuhn-Tucker-Bedingungen dafür verwenden einen Lagr.Parameter λ; sie lauten:
∂K
∂K
− λ ai ≤ 0, xi ≥ 0, xi · pi − ∂x
− λ ai = 0 für i = 1, . . . , n
pi − ∂x
i
i
λ · c − a x = 0
c − a x ≥ 0, λ ≥ 0,
Um diese Bedingungen zu interpretieren, erinnern wir uns, dass der Lagrange-Parameter
λ∗ angibt, um welchen Betrag der Gewinn bei Erhöhung der Ressourcenkapazität c um
eine Einheit steigen würde; dies ist der (Schatten-)Preis, den das Unternehmen für eine
Einheit der Ressource höchstens zu zahlen bereit wäre, müsste es sie extern einkaufen.
Die Größe λ ai multipliziert diesen Preis (einer Ressourceneinheit) mit der Zahl der für
eine Outputeinheit benötigten Ressourceneinheiten. Die Größe λ∗ ai stellt also die Kosten
dar, die zur Prod. einer Einheit des i-ten Gutes anfallen würden, wenn das UN die Ressource zum Preis λ∗ kaufen würde. In der ersten Zeile der KT-Bedingungen werden diese
‘Schatten-Grenzkosten’ zu den eigentlichen Grenzkosten hinzuaddiert.
Damit ergibt sich folgende Sichtweise auf die erste Zeile der KT-Bedingungen: Obwohl die
Ressource keine (direkten) Kosten verursacht, wirkt ihre Beschränkung wie ein Kostenfaktor für das UN. Das UN agiert nach wie vor nach der Devise (exogener) Preis = (interne)
”
Grenzkosten“, allerdings müssen in die Grenzkosten die Schatten-Grenzkosten der Ressourcenbeschränkung einbezogen werden. Güter, deren (gesamte) Grenzkosten über dem
Preis liegen, werden nicht produziert (xi = 0). Die zweite Zeile besagt im Wesentlichen:
Wenn die vorhandene Kapazität c der Ressource noch nicht erschöpft ist, dann ist ihr
Preis λ∗ gleich 0: Nur wenn die Ressource knapp ist und das UN somit einen Anreiz hat,
Ressourceneinheiten hinzuzukaufen, entsteht ein positiver Schattenpreis der Ressource.
3
Dies ist wiederum etwas vereinfacht, da Interaktionseffekte bei den Produktionskosten ignoriert werden: Eine
partielle Erhöhung von xi kann auch die Grenzkosten der anderen Produkte beeinflussen. Die KT-Bedingungen
erfassen auch dies.
c K.H. Schild, Abt. Statistik, Fb. Wiwi, Uni Marburg
3.8
35
KT-Bedingungen in der linearen Optimierung; Dualität
Wir betrachten nun den Spezialfall einer linearen Zielfunktion f (x) = p x unter linearen Re
striktionen gj (x) = aj x ≤ cj , d.h. A x ≤ c (wobei A die m×n Matrix mit den Zeilen a1 , . . . , am
ist). D.h. wir betrachten nun das lineare Optimierungsproblem
maxn p x u. d. Nbdg. A x ≤ c, x ≥ 0
x∈R
(P)
Ohne auf die Details einzugehen, sei zunächst erwähnt, dass für solche Probleme mit dem Simplexverfahren ein sehr effizientes Lösungsverfahren zur Verfügung steht. Anstelle des systematischen Vorgehens basierend auf allen Kombinationen von bindenden und nicht-bindenden
Restriktionen kann man sich beim linearen Problem (P) von vorneherein auf Basis-Lösungen“
”
beschränken, wo n Komponenten aus dem n+m-dimensionalen (x, Ax−c) gleich 0 sind (die Basis
entspricht den verbleibenden m Komponenten). Denn die zulässige Menge ist hier ein konvexes
Polyeder, und das Optimum wird (wenn überhaupt, dann) in einer Ecke des zulässigen Polyeders
angenommen. In einer solchen Ecke binden n der insgesamt m + n linearen Restriktionen (wenn
k der m Restriktionen a
j x − cj binden, dann kommen n − k der n Nicht-Neg.-Bedingungen als
bindende Restriktionen hinzu); die restlichen m Restriktionen sind durch das n-dimens. x normalerweise nicht als Gleichungen erfüllbar (sondern nur als echte Ungleichung, und dann kann es
sein, dass die Basis nicht zulässig ist.) Das Simplexverfahren verknüpft diese Überlegungen mit
einer effizienten Suchtechnik (Pivotstrategie) nach verbesserten zulässigen Basen bzw. Ecken.
Die Kuhn-Tucker-Bedingungen für das Problem (P) lauten (in Vektor-Schreibweise):
p − A λ ≤ 0, x ≥ 0, x · p − A λ = 0 (Vektoren d. Dim. n)
c − A x ≥ 0, λ ≥ 0, λ · c − A x = 0 (Vektoren d. Dim. m)
Beim zu (P) dualen Problem (D) wird statt eines Maximierungs- ein Minimierungsproblem mit
vertauschten Rollen von Zielfkts-Koeffizienten p und Restriktions-Inhomogenität c betrachtet,
so dass ein Problem in m Variablen mit n Restriktionen entsteht. Die Restriktion wird mit A
statt A und ≥ statt ≤-Relation gebildet:
min c y u. d. Nbdg. A y ≥ p, y ≥ 0
y∈Rm
(D)
Mit μ = (μ1 , . . . , μn ) als Lagrange-Parametern lauten die KT-Bedingungen dazu:
c − A μ ≥ 0, y ≥ 0, y · c − A μ = 0 (Vektoren d. Länge m)
p − A y ≤ 0, μ ≥ 0, μ · p − A y = 0 (Vektoren d. Länge n)
Ersetzen wir die Variablen y des dualen mit den Lagr.Multiplikatoren λ des primalen Problems
(P) und die Lagr.Multiplikatoren μ des dualen mit den Variablen x des primalen Problems,
so zeigt ein Vgl: Die KT-Bedingungen des dualen stimmen mit denen des primalen
Problems mit vertauschten Rollen von Variablen und Lagr.Multiplikatoren überein.
Die λ∗ des primalen Problems minimieren also c λ unter den Restriktionen λ ≥ 0, A λ ≥ p.
Zur Interpretation dieses Ergebnisses sei wieder ein Unternehmen betrachtet, das n Güter in den
Mengen x1 , . . . , xn produziert, die es zu den Preisen p1 , . . . , pn absetzen kann. Zur Produktion
benötigt das Unternehmen m Ressourcen (Inputfaktoren), die ihm (zwar kostenlos, aber) in
beschränkten Mengen c1 , . . . , cm zur Verfügung stehen; zur Produktion einer Einheit des Gutes
i werden aj,i Einheiten der j-ten Ressource benötigt. Ziel des Unternehmens ist die Maximierung
des Gewinns (=Erlös − Kosten) unter Einhaltung der Ressourcenkapazitäten. Wenn dem UN
36
Statische Optimierung – Kuhn-Tucker
keinerlei (direkte) Produktionskosten entstehen, fällt der Gewinn mit dem Erlös p x zusammen,
und das Problem hat die Struktur (P). Wie im vorhergehenden Abschnitt erzeugen diejenigen
Ressourcen, die knapp sind, ’Schattenkosten’ für das UN. Die obige Dualitätsaussage läuft darauf
hinaus, dass man die Maximierung des Gewinns äquivalent als Minimierung der Schattenkosten
sehen kann. Dies soll noch einmal im Detail erläutert werden:
Der j-te Lagrange-Parameter λ∗j gibt an, um welchen Betrag der Erlös p x∗ bei Erhöhung der
j-ten Ressource cj um eine Einheit steigen würde; dies ist der (Schatten-)Preis, den das Unternehmen für eine Einheit der Ressource höchstens zu zahlen bereit wäre, müsste es sie extern
einkaufen (λ∗j = 0 bedeutet, dass die im UN vorhandene Menge der j-ten Ressource nicht knapp
ist). Die Größe c λ∗ stellt also die Kosten dar, die dem UN entstehen würden, wenn es die
Ressourcen nicht hätte, sondern sie zu den Preisen λ∗j einkaufen müsste (Opportunitätskosten,
Schattenkosten). Wie oben aus der Dualitätstheorie gefolgert, werden diese minimiert unter der
Restriktion A λ∗ ≥ p (wobei komplementärer Schlupf zu x entsteht). Der i-te Eintrag von
A λ∗ gibt die Kosten zur Produktion einer Einheit des i-ten Produkts an, die anfallen würden,
wenn man die Ressourcen nicht hätte, sondern sie zu den Preisen λ∗j einkaufen würde. Sie stellen
die ‘Schatten-Grenzkosten’ der Produktion dar (hier Grenzkosten = Stückkosten). Die komplementäre Schlupfbed. bzgl. xi und (A λ)i − pi besagt, dass Güter i, deren Schatten-Grenzkosten
(A λ∗ )i über dem Verkaufspreis pi liegen, nicht produziert werden (x∗i = 0), während bei den
effektiv produzierten Güter (x∗i > 0) die Schatten-Grenzkosten gerade dem Verkaufspreis pi
entsprechen.
Neben der Eigenschaft, dass die ‘Schattenpreise’ λ∗ des primalen Problems die Zielfunktion
c λ des dualen Problems unter dessen Restriktionen minimieren, besteht ein weiterer allgemeiner Zusammenhang zwischen den beiden Problemen: Die Optimalwerte (erreichbare
Zieffkts.Werte) von primalem und dualem Problem sind gleich: Ihr gemeinsamer Wert
ist λ∗ A x∗ , denn die kompl.Schlupfbed. bzgl λ im primalen Problem implizieren, dass c λ∗ =
λ∗ c = λ A x, diejenigen bzgl. μ im dualen Problem, dass p μ = μ p = μ A y = y A μ.
Da y ∗ = λ∗ und μ∗ = x∗ , ergibt sich beide Male als Zielfktswert λ∗ A x∗ . Einmal liest man
diesen Wert als Skalarprodukt der beiden m-dimens. Vektoren λ und A x (wobei λj = 0, falls
(Ax)j < cj und (Ax)j = cj , falls λj > 0), einmal als Skalarprodukt der beiden n-dimens.
Vektoren λ A und x (wobei xi = 0, falls (λ A)i > pi und (λ A)i = pi , falls xi > 0).
Die Symmetrie oder Dualität in den Rollen der Variablen (xi ) und Lagrange-Multiplikatoren (λj ) findet man auch in den ursprünglichen KT-Bedingungen (wo die LagrangeMultiplikatoren μi der Nicht-Neg.-Bedingungen noch nicht eliminiert waren), wenn man – wie im
üblichen Simplexverfahren – für die ‘normalen’ Restriktionen Schlupfvariablen yj := cj − a
jx
einführt, die wie die ‘normalen’ Variablen xi behandelt werden. Dann unterliegen sämtliche
Vektoren Nicht-Neg.-Bedingungen, x ≥ 0, y ≥ 0, λ ≥ 0, μ ≥ 0, mit komplement. Schlupf
zwischen x und μ sowie y und λ, d.h. μ x = 0 und λ y = 0. Außerdem gelten die Gleichungen
Ax + y = c sowie A λ − μ = p, die sich mit Hilfe von Block-Vektoren bzw. -Matrizen in
folgender ‘dualen’ Form schreiben lassen:
A
x
λ
A, Im
= c,
A , −In
= p (bzw. λ , μ
= p )
y
μ
−In
Beachte: (1) Die Größen y und μ sind hier Schlupfvariablen, sie haben nicht die gleiche Bedeutung wie im dualen Problem (D). (2) Das übliche Simplexverfahren behandelt das primale
Problem (P) und beruht auf der linken Form. (3) Aus dem Endtableau des üblichen Simplexverfahrens kann man bereits die Lagrange-Multiplikatoren λ ablesen; das duale Simplexverfahren,
das vom Problem (D) ausgeht und der re. Form entspricht, wird dazu also nicht benötigt.
Viele der in diesem Abschnitt für lineare Optimierungsprobleme formulierten Dualitätsaussagen
gelten auch für nicht-lineare Probleme.