4. Energie, Arbeit, Leistung

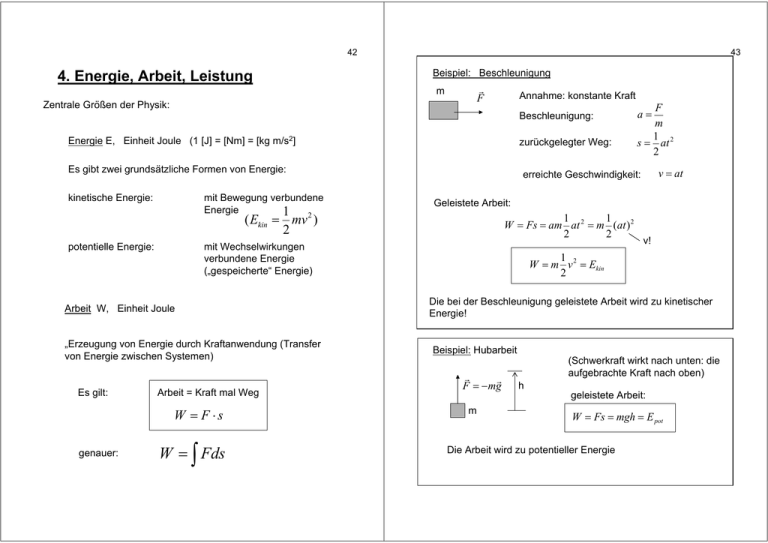
42
4. Energie, Arbeit, Leistung
43
Beispiel: Beschleunigung
F
m
Zentrale Größen der Physik:
Annahme: konstante Kraft
Beschleunigung:
Energie E, Einheit Joule (1 [J] = [Nm] = [kg m/s2]
zurückgelegter Weg:
Es gibt zwei grundsätzliche Formen von Energie:
kinetische Energie:
mit Bewegung verbundene
Energie
1 2
Geleistete Arbeit:
„Erzeugung von Energie durch Kraftanwendung (Transfer
von Energie zwischen Systemen)
Es gilt:
Arbeit = Kraft mal Weg
W = F ⋅s
genauer:
1
1
W = Fs = am at 2 = m (at ) 2
2
2
mit Wechselwirkungen
verbundene Energie
(„gespeicherte“ Energie)
Arbeit W, Einheit Joule
W = ∫ Fds
v = at
erreichte Geschwindigkeit:
( Ekin = mv )
2
potentielle Energie:
F
m
1
s = at 2
2
a=
v!
1
W = m v 2 = Ekin
2
Die bei der Beschleunigung geleistete Arbeit wird zu kinetischer
Energie!
Beispiel: Hubarbeit
F = − mg
m
(Schwerkraft wirkt nach unten: die
aufgebrachte Kraft nach oben)
h
geleistete Arbeit:
W = Fs = mgh = E pot
Die Arbeit wird zu potentieller Energie
44
Beispiel: Spannen einer Feder
x
45
Gleiche Arbeit! Die Potentielle Energie hängt nicht davon
ab, wie sie erzeugt wurde!
Kraft einer Feder
(Hook‘sches Gesetz)
F = − Dx
l
Allgemein:
W = F ⋅s
geleistete Arbeit:
l
∫
∫
(für geraden Weg
und konstante Kraft)
r
l
1
W = Fdx = ( Dx)dx = D l 2 = E pot
2
0
0
Vektorielle Beschreibung
genauer:
W = F ( r ) ds
∫
=
r0
i
Arbeit wird zu potentieller Energie
4.1 Wegunabhängigkeit der pot. Energie
Beispiel: schiefe Ebene
m
Arbeit: direktes Heben
W = mgh = E pot
F
Arbeit: über Rampe
F
l
α
F⊥
h
W = Fs
= mg sin α l
h
= mg sin α
= mgh
sin α
∑
Fi ∆si
(für gerade
Teilstücken)
Beispiel: Hubarbeit im Schwerefeld (ortsunabhängige Kraft)
 0  ∆x 
n   i 
W = ∑ F∆si =∑  0  ∆yi 
i =1
i =1 


 mg  ∆zi 
n
=
n
∑ mg∆z
i =1
i
=mg
n
∑ ∆z
i
= mgh
i =1
Eine Bewegung in x- oder y-Richtung spielt keine Rolle; es zählt
nur die Bewegung in Richtung der Kraft.
46
r1
Bedeutung von
W = ∫ F ( r ) ds :
Linienintegral
47
Bemerkung: das Kraftfeld ist der negative Gradient der
potentiellen Energie
r0
F
r1
Weg
F
r0
Im Schwerefeld:
ds
ds
r1
F ds =
r0
Kraftfeld
F (r ) = −∇E pot
an jedem Ort Skalarprodukt
r1
r0
=
F ⋅ ds



0
dx
 0   dy 
mg
dz
r1
∂

 E pot 
 ∂x

∂

E 
=−
 ∂y pot 
∂

 E pot 
 ∂z

Ein so gebildetes Kraftfeld ist immer konservativ!
Beispiel: Schwerefeld
mgdz = mg∆z
 0 


F = −∇E pot = −∇(mgz ) =  0 
 − mg 


r0
Arbeit hängt nur vom
Höhenunterschied ab!
Für ein nichtkonservatives Kraftfeld gilt:
Definition:

Ein Kraftfeld, bei dem das Integral
r
∫ F ( r ) ds
r0
× F = 
∇
Es gilt:
nur von Anfangs- und Endpunkt, aber nicht
vom Weg abhängt, heißt konservativ.
∂
∂x
∂
∂y
∂
∂z


 × F = 

∂Fy
∂z
∂Fx
∂z
∂Fy
∂x
−
−
−
∂Fz
∂y
∂Fz
∂x
∂Fx
∂y


 = 0
∇ × (∇ φ ) = 0
⇒ ein als Gradient eines Skalarfelds gebildetes Kraftfeld ist
immer konservativ!
48
Definition:
Potential
V (r ) = E pot (r )
r
Damit also
V (r ) = ∫ − Fs ( r ) ds
49
4.2 Energieerhaltung
Für ein abgeschlossenes System gilt:
Ekin + Epot = konstant
r0
im System wirkende Kraft
Da r0 frei wählbar ist, ist das Potential nur bis auf eine additive
Konstante definiert.
Es gilt damit:
Fs (r ) = −∇V (r )
Die Summe der kinetischen und der potentiellen Energie
ist konstant; sie ändert sich nur, wenn Arbeit am System verrichtet
wird.
Aber: potentielle Energie kann in kinetische Energie umgewandelt
werden und umgekehrt
Beispiel: freier Fall
nachher:
vorher:
h
Die Kraft ist der negative Gradient des Potentials.
m
h
m
Eigenschaften:
der Gradient zeigt in die Richtung maximaler
positiver Steigung; er steht senkrecht auf
den Äquipotentiallinien bzw. –flächen.
⇒ die Kraft zeigt in die Richtung maximaler
negativer Steigung des Potentials („bergab“)
E pot = mgh
E pot = 0
m
Ekin = v 2
2
Ekin = 0
Mit der Energieerhaltung folgt:
und damit:
mgh =
v = 2 gh
m 2
v
2
v
50
nachrechnen:
51
Körper am äußeren Umkehrpunkt:
zeitabhängige Höhe beim Fall
Zeit beim Erreichen von z=0
Geschwindigkeit hier
1
z (t ) = h − gt 2
2
2h
t=
g
1 2
Ekin = mvmin
=0
2
kinetische Energie ist minimal
1 2
1
E pot = Dxmax
= Dx02
2
2
potentielle Energie ist maximal
v = gt = 2 gh
Wegen der Energieerhaltung gilt damit:
Gleiches Ergebnis!
1
1
2
m( x0ω ) 2 = Dx0
2
2
Beispiel: harmonische Schwingung
m
mω 2 = D
x(t ) = x0 cos ωt
ω=
v (t ) = x0ω sin ωt
D
m
Schwingungsfrequenz
Federpendel
x
Ständiges Umwandeln von potentieller in kinetische Energie
und umgekehrt.
Andere Herleitung:
es ist
Körper in der Mitte:
kinetische Energie ist maximal
potentielle Energie ist minimal
1 2
m
Ekin = mvmax
= ( x0ω ) 2
2
2
1 2
E pot = Dxmin
=0
2
also
Es gilt
das heißt
also
a (t ) = − x0ω 2 cos ωt
a = −ω 2 x (t )
F = ma
− Dx = −mω 2 x
ω=
D
m
52
4.3 Leistung
53
4.4 Dissipation: Reibung
Leistung ist Arbeit pro Zeit
Einheit Watt
Die vollständige Umwandlung von Arbeit an einem Körper in
kinetische und potentielle Energie des Körpers
[W] = [J/s]=[Nm/s]
P=
W
t
dW
P=
dt
genauer:
Geleistete Arbeit ist
W = ∆Ekin + ∆E pot
bzw. die Energieerhaltung, wenn keine Arbeit geleistet wird
Ekin + E pot = konstant
gilt nur bei Abwesenheit disspativer Effekte (Reibung)
Es folgen Beispiele für Reibung.
W = Pt
4.4.1. Coulomb-Reibung (Oberflächen-Reibung)
t
bzw.
W = ∫ Pdt
FR
v
m
0
Beispiel: Hubarbeit
10 kg werden um 10 m angehoben
W = mgh ≈ 1000 J
W 1000 J
geleistet in 5 min (300s):
P= =
= 3.3W
t
300s
1000 J
geleistet in 10 s:
P=
= 100W
10s
F⊥
Klotz bewegt sich mit Geschwindigkeit
v parallel zur Oberfläche.
Für die Reibungskraft gilt:
v
FR = µ F⊥ (− )
v
Gleitreibung
Arbeit:
Reibungskoeffizient
Anpresskraft
Richtung
der Bewegung
entgegengesetzt
54
Folgerungen:
Ausnahme:
Körper ruht:
- Kraft ist unabhängig von der Geschwindigkeit
- Kraft ist unabhängig von der Auflagefläche
- Stärke wird nur bestimmt durch Anpresskraft
und Materialkombination
Fa
FR = µ ' F⊥ ( − )
Fa
Stahl auf Stahl
(poliert)
Typische Werte:
Gummi auf Asphalt
µ ' ≈ 0.7
µ ≈ 0.4
µ ' ≈ 1.2
µ ≈ 1.0
Mikroskopisch sind Flächen nie glatt.
Jedes Material verformt sich ab einem
kritischen Druck pkrit.
⇒ an den Berührpunkten verformen
sich die Spitzen, bis der kritische
Druck unterschritten wird:
Fläche A
F⊥
Berührpunkte
(Kontaktfläche A*)
⇒
trocken
naß
Beispiel: maximal mögliches Beschleunigen eines Autos
Drehende Räder können maximal die Haftreibungskraft auf die
Straße ausüben, blockierende Räder die Gleitreibungskraft.
Die maximal mögliche (positive oder negative!) Beschleunigung
ist damit:
bzw.
Warum ist die Reibung unabhängig von der Auflagefläche A?
Haftreibung
µ ' ≈ 0.6
µ ≈ 0.4
a=
55
FR µF⊥ µ mg
=
=
= µg
m
m
m
F'
a' = R = µ ' g
m
Ein Fahrzeug mit Gummireifen kann auf Asphalt also
mit maximal 1.2 g beschleunigen!
pkrit =
F⊥
A*
A* =
F⊥
pkrit
Die tatsächliche Kontaktfläche ist für eine gegebene Andruckkraft
immer gleich, und unabhängig von der Fläche A!
⇒ die Reibungskraft ist unabhängig von A
4.4.2. Newton-Reibung
FR
v
Schneller Körper in leichter Flüssigkeit
oder Gas
Hier gilt für die Reibungskraft:
1
v
2
F = cW ρ Av (− )
2
v
v
Geschwindigkeit
cW
Widerstandsbeiwert des Körpers
A
Querschnittsfläche des Körpers
(senkrecht zur Geschwindigkeit)
56
Die Kraft ist proportional zum Quadrat der Geschwindigkeit!
57
dW = Fds = Fvdt = dE
geleistete Arbeit
Bei der Bewegung aufgebrachte Leistung:
⇒
P=
Fs
1
= Fv = cW ρ Av 3
t
2
Beispiel: Auto
A = 2.5 m2
ρ = 1.29 kg/m3 (Luft)
cW = 0.3
v = 100 km/h (27.8 m/s) :
F = 374 N
P = 10393 W ( = 14 PS)
v = 200 km/h (56 m/s) :
F = 1495 N
P = 83146 W ( = 113 PS)
Anahme: ein Körper beschleunigt alles Gas in seiner Bahn auf
seine Geschwindigkeit. Im Zeitintervall dt ist:
durchstrichenes Volumen
beschleunigte Gasmasse
erzeugte kinetische Energie
Nicht alles Gas wird beschleunigt; wird durch Faktor cw
berücksichtigt.
Unter Anwesenheit von Reibung wird ein Teil der geleisteten
Arbeit in Wärmeenergie umgewandelt:
W = ∆Ekin + ∆E pot + ∆EW
Definition: Wärmeenergie ist die Differenz zwischen tatsächlicher
und minimal möglicher mittlerer potentieller und kinetischer
Energie der Atome eines Systems
Ebenso kann kinetische Energie direkt in Wärmeenergie
umgewandelt werden
Herleitung Newton-Reibung
zurückgelegte Strecke
1
F = ρ Av 2
2
Kraft
ds = vdt
dV = Ads = Avdt
dM = ρ dV = ρ Avdt
1
1
dE = v 2 dM = v 2 ρ Avdt
2
2
−∆Ekin = ∆EW
⇒ es gilt eine erweiterte Energieerhaltung
Ekin + E pot + EW = konstant
Beispiel: Klotz auf Ebene
m
Fa
Klotz ruht am Ende:gesamte Arbeit wird
in Wärmeenergie umgewandelt
W = Fl = µ mgl = ∆EW
58
59
4.5 Impuls
F = ma
dv
a=
dt
mit
Weitere zentrale Größe!
mit
Herleitung aus Reaktionsprinzip (hier für zwei Körper)
m1
F1
F2
m2
actio = reactio
F2 = − F1
Die Kräfte führen zur Beschleunigung beider Körper;
die gesamte kinetische Energie wächst kontinuierlich
Die an jedem Körper pro Zeitintervall verrichtete Arbeit ist
dWi dEkin ,i
= vi Fi =
dt
dt
mit
vi Fi
:
dEkin ,i
= vi Fi
dt
Zunahme der gesamten kinetischen Energie:
dEkin
= v1 F1 + v2 F2
dt
also
m2 a2 = − m1a1
v2
v1
m2 = −m1
dt
dt
d
(m1v1 + m2 v2 ) = 0
dt
bleibt konstant!
m1v1 + m2 v2
Definition:
p = mv
Impuls:
⇒ die Summe der Impulse beider Körper bleibt konstant!
Für einen einzelnen Körper gilt:
t
t F (t )
v (t ) = v0 + ∫ a (t )dt = v0 + ∫
dt
m
0
0
Mutipliziert mit m:
t
p(t ) = p0 + ∫ F (t )dt
0
Aber es gibt eine Erhaltungsgröße:
Es gilt
F2 = − F1
Bei konstanter Kraft und
p0 = 0
p = F ⋅t
Impuls ist
Kraft mal Zeit!
60
4.7 Stöße
4.6 Impulserhaltung
actio = reactio gilt auch für ein System aus beliebig
vielen Körpern:
m1
m2
F1
F
3
F2
F6
m3
Stoß:
Austausch von Impuls und Energie zwischen Körpern
in endlichen Zeitintervallen; keine Wechselwirkung im
Anfangs- und Endzustand.
Anfangszustand
m4
F5
61
∑ Fi = 0
N
F4
i =1
p1 , p2 , p3 ...
Endzustand
p '1 , p'2 , p '3 ...
Wechselwirkung
E1 , E2 , E3 ...
E '1 , E '2 , E '3 ...
m5
Es gilt:
m6
∑ p =∑ p '
i
Für die Summe der Impulse gilt:
t
t
N
N
0
0 N ∑ pi = ∑ ( pi + ∫ Fi dt ) = ∑ pi + ∑ ∫ Fi dt
Impulserhaltung
i
N
i =1
i =1
t0
i =1
t N
= pges + ∫ ∑ Fi dt
t0 i =1
= pges
elastischer Stoß:
i =1 t0
Dann gilt
keine Umwandlung von kinetischer Energie
in potentielle oder Wärmeenergie
(keine Anregung „innerer Freiheitsgrade“ der
Körper)
∑E
kin
i
=∑ E kin 'i
Energieerhaltung
=0
In einem System, auf das keine äußeren Kräfte wirken,
ist der Gesamtimpuls eine Erhaltungsgröße
4.7.1 Zentraler elastischer Stoß zwischen zwei Körpern
Zentraler Stoß: gesamte Bewegung findet auf einer Geraden statt
m1
v1
v2
m2
62
Impulserhaltung:
m1v1 + m2v2 = m1v '1 + m2v '2
eindim. Bewegung:
m1v1 + m2v2 = m1v '1 + m2v '2
63
⇔
m22 + m1m2 2
v1v'2 =
v '2
2m1
⇔
v'22 =
kin. Energieerhaltung:
1
1
1
1
m1v12 + m1v2 2 = m1v '12 + m2v '2 2
2
2
2
2
Für diese Gleichung gibt es zwei Lösungen:
Lösung 1:
Zwei Gleichungen, zwei Unbekannte (v‘1, v‘2)
Dann gilt:
Lösung 2:
Einsetzen:
⇔
⇒
v '1 = v1 −
m2
v '2
m1
1
1
2
2 1
2
m1v1 = m1v'1 + m2 v '2
2
2
2
und
⇔
m1v1 = m1v '1 + m2v '2
v '2 = 0
v'1 = v1
(„Triviale“ Lösung: Stoß hat nicht stattgefunden)
⇒ eindeutige Lösung für gegebene Parameter m1, v1, m2, v2
(unabhängig von der Art der Wechselwirkung!)
Beispiel: zweiter Körper ruht (v2 = 0)
2m1
v1v'2
m1 + m2 1
2m1
v1
m1 + m2
m
m − m2
v'1 = v1 − 2 v'2 = 1
v1
m1
m1 + m2
v '2 =
Diskussion dieses Resultats für verschiedene Fälle:
2
 1
1
1 
m
m1v12 = m1  v1 − 2 v '2  + m2v '2 2
2
2 
m1  2
1
1
m 2m
m m2
1
m1v12 = m1v12 − 1 2 v1v '2 + 1 22 v '22 + m2v '2 2
2
2
2 m1
2 m1
2
m22 2 1
0 = −m2v1v '2 +
v '2 + m2v '2 2
2m1
2
1. m1 = m2
hier gilt:
v'2 = v1
v'1 = 0
Der Impuls (und die kinetische Energie) werden
vollständig auf den gestoßenen Körper übertragen.
64
2. m1 << m2
hier gilt:
2m
v'2 ≈ 1 v1
m2
v'1 ≈ −v1
( p '2 ≈ 2 p1 !)
65
3. m1 >> m2
hier gilt:
Der stoßende Körper wird kaum verlangsamt; der
gestoßene Körper erhält die doppelte
Geschwindigkeit des stoßenden Körpers!
v'2 ≈ 2v1
v'1 ≈ v1
Allgemein: dreidimensionaler Stoß
Der stoßende Körper wird kaum verlangsamt; der gestoßene
Körper erhält die doppelte Geschwindigkeit des stoßenden
Körpers!
m1
Effizienz der Energieübertragung:
Hier gilt:
2
m  2m1  2
1
E '2 = m2 v '2 2 = 2 
v1
2
2  m1 + m2 
m2
4m12
4m1m2 m1 2
=
v2 =
v1
2 1
2 (m1 + m2 )
(m1 + m2 ) 2 2
E2 ' =
v'2 ≈ 2v1
v'1 ≈ v1
Der stoßende Körper wird reflektiert; der gestoßene Körper
erhält den doppelten Impuls des stoßenden Körpers!
3. m1 >> m2
hier gilt:
4m1m2
E1
(m1 + m2 ) 2
Maximal für m1 = m2 ! (hier ist E2‘ = E1)
Für m1≠ m2 ist E2‘ < E1; der gestoßene Körper erhält nur einen
Teil der Energie des stoßenden Körpers.
v1
v2
m2
m1v1 + m2 v2 = m1v '1 + m2 v '2
Impulserhaltung
1 2 1 2 1 2 1 2
m1 v1 + m2 v2 = m1 v '1 + m2 v '2
2
2
2
2
Energieerhaltung
Dies sind 4 Gleichungen mit 6 Unbekannten (
v '1 , v '2
)
⇒ Lösung bestimmt bis auf zwei freie Parameter!
(z.B. legt die Wahl der Richtung von
fest)
v1
alle anderen Werte
66
67
Jetzt: Rakete
4.7.3 Anwendung der Impulserhaltung: Rakete
vw
m1
v '2
m2
m1
Person in Boot in Ruhe wirft eine
Kugel mit Wurfgeschwindigkeit
vw (Geschwindigkeit relativ
zur Person)
Dadurch erhält das Boot (und
die Person) einen Impuls bzw.
eine Geschwindigkeit in
Gegenrichtung
Es gilt:
v '1 + v '2 = vW
Impulserhaltung:
m1v '1 = m2 v '2
v
m
vD
Vortrieb durch Wurf:
m2
v '1
heiße Gase
In der Zeit dt wird die Masse
dmGas mit Geschwindigkeit
vDausgestoßen.
Ausstoß führt zur Abnahme der
Raketenmasse:
Brennkammer und
Düse
Treibstoff
dmGas = - dmR
Geschwindigkeitsänderung der Rakete dadurch (dmR << mR) :
dv =
dmGas
dm
vD = − R v D
mR
mR
Umformen:
v
dv
=− D
dm
m
Integration über m:
m
m1v '1 = m2 (vW − v '1 )
also
⇒
Für m1 << m2 wird dies zu:
v '1 =
m2
vW
m1 + m2
v '2 =
m1
vW
m1 + m2
v '1 ≈ vW
und
∫
m0
⇒
m
dv
1
dm = −
vD dm
dm
m
m
∫
0
v(m0 ) − v(m) = −vD (ln(m) − ln(m0 )) = vD ln(
m0
)
m
Falls v(m0) = 0 ist (Startgeschwindigkeit Null):
v '2 ≈
m1
vW
m2
v = vD ln(
m0
)
m
Raketengeschwindigkeit
Ausstoß von Masse erzeugt Vortrieb!
Gasgeschw.
Verhältnis Start- zu Endmasse
68
Die von einer Rakete erreichbare Geschwindigkeit hängt von dem
Verhältnis der Start- und Endmasse und der Gasgeschwindigkeit ab.
vD = 2000
nachher:
m
s
vEnd ≈ 3600 ms
Damit:
„Reibungseffekte“ (Umwandlung kinetischer Energie in
Wärmeenergie) verändern Stöße.
m2
m1
⇔
⇔
v '1 = v '2
Kugeln bleiben zusammen
Dämpfer
Es gilt:
m2
Pges = P ' ges
Impulserhaltung (gilt immer!)
m1v1 = m1v '1 + m2 v '2 = (m1 + m2 )v '1
v '1 =
m1 v1
m1 + m2
m1
Ekin
m1 + m2
Die kinetische Energie wird verringert !
Die „fehlende Energie wird in Wärmeenergie verwandelt:
Beispiel: vollinelastischer zentraler Stoß
v1
E 'kin
1
Ekin = m1v12
2
1
1
1
= m1v '12 + m2 v '22 = (m1 + m2 )v '12
2
2
2
m1
1 m12
v12 =
Ekin
=
2 m1 + m2
m1 + m2
E 'kin =
4.7.4 Inelastischer Stoß
m1
Für die kinetische Energie gilt:
vorher:
m0
=6
m
Typische Werte:
69
Vollinelastischer
Stoß
E 'W = EW + Ekin − E 'kin
= EW +
m2
Ekin
m1 + m2
Merke: bei inelastischen Prozessen gilt Impulserhaltung, aber
nicht die Erhaltung der kinetischen Energie! (sondern
nur die Erhaltung der Gesamtenergie)
70
4.7.4 Stöße in 3D
4.8 Schwerpunkt
Stoß zwischen zwei Körpern mit beliebigen Geschwindigkeiten
m1
Hier gilt:
71
v1
v2
Definition:Schwerpunktskoordinate eines Systems aus
N Massenpunkten
N
m2
rs =
m1v1 + m2 v2 = m1v '1 + m2 v '2
Schwerpunkt:
„Gewichtetes Mittel
der Ortskoordinaten“
i i
i =1
N
∑m
i
i =1
Impulserhaltung
(3 Gleichungen!)
∑m r
Bewegung des Schwerpunkts:
N
Bei einem elastischen Stoß:
rɺɺs =
1 2 1
2 1 2 1 2
m1 v1 + m2 v2 = m1 v '1 + m2 v '2
2
2
2
2
∑ m rɺɺ
i i
i =1
N
=
∑m
i
i =1
∑m
a
∑ (F + F
N
i =1
N
1
i
i =1
i
)
i
äußere Kräfte
Energieerhaltung
(1 Gleichung)
Dies sind 4 Gleichungen mit 6 Unbekannten (
beiden Vektoren haben je 3 Komponenten)
v '1 , v '2
N
mit
i =1
; die
∑F
i
=0
(Reaktionsprinzip)
N
und den Bezeichnungen
i =1
⇒ Lösung bestimmt bis auf zwei freie Parameter!
(z.B. legt die Wahl der Richtung von
fest)
v1 '
a
∑F
i
N
∑m
i =1
alle anderen Werte
gilt also:
a
ɺɺ Fges
rs =
M
i
a
=Fges
gesamte äußere
Kraft
=M
Gesamtmasse
Der Schwerpunkt bewegt sich
wie ein Massenpunkt mit der
Gesamtmasse des Systems,
an dem sämtliche Kräfte angreifen!
72
Folgerung: ohne äußere Kräfte ändert der Schwerpunkt eines
Systems seinen Bewgungszustand nicht!
73
Für die kinetische Energie im Schwerpunktsystem gilt:
N
E
4.9 Schwerpunktsystem
vs = rɺs =
i =1
N
i i
∑m
i =1
=
1
M
N
∑m v
i =1
1
ges
= Ekin
− vs Mvs + M vs
2
1
2
ges
= Ekin
− M vs
2
i i
i
Galilei-Transformation in das Schwerpunktsystem:
2
2
1
2
ges
s
Ekin
= M vs + Ekin
2
Umgeformt:
ri s = ri − rs
vis = vi − vs
2
N
mi 2 N mi m vi − ∑ 2vi vs + ∑ i vs
i =1 2
i =1 2
i =1 2
N
N
1 2
ges
= Ekin
− vs ∑ mi vi + vs ∑ mi
2
i =1
i =1
=∑
Geschwindigkeit des Schwerpunkts:
∑ m rɺ
mi s 2 N mi = ∑ vi = ∑ vi − vs
i =1 2
i =1 2
N
Das Schwerpunktsystem ist ein Koordinatensystem, dessen
Ursprung der Schwerpunkt des Systems ist.
N
s
kin
Relativkoordinaten!
kin. Energie
aller Körper
kin. Energie
„des Schwerpkts.“
„innere“
kin. Energie
des Systems
Für den Gesamtimpuls im Schwerpunktsystem gilt:
N
N
s
pges
= ∑ mi vis = ∑ mi (vi − vs )
i =1
i =1
N
N
= ∑ mi vi − vs ∑ mi = Mvs − vs M = 0
i =1
i =1
Des Gesamtimpuls im Schwerpunktsystem ist Null!
Die kinetische Energie läßt sich aufteilen in die kinetische Energie
der Bewegung des Gesamtsystems und der Bewegung im
Schwerpunktsystem!
Beispiel: Stoß, zwei Körper gleicher Masse, 2. Körper ruht
v1
m1
vs
m2
m1v1 + m2 v2 1 vs =
= v1
m1 + m2
2
74
Im Schwerpunktsystem gilt:
75
Bewegung im Laborsystem nach dem Stoß:
1
v1s = v1 − vs = v1
2
1
v2s = v2 − vs = − v1
2
v1 ' = v1s '+ vs
v2 ' = v2s '+ v1s
v1s = −v2s
v1 '
Bei dem Stoß im Schwerpunktsystem gilt Impulserhaltung:
α
m1v1s '+ m2 v2s ' = m1v1s + m2 v2s = 0
v1s ' = −v2s '
also auch
vs
v2 '
In diesem Fall haben die
Endgeschwindigkeiten im
Laborsystem zueinander einen
Winkel von 90°!
(Thaleskreis!)
v1s '
v2 s '
Beim elastischen Stoß gilt Energieerhaltung:
1
2 1
2 1
2 1
m1 v1s ' + m2 v2 s ' = m1 v1s + m2 v2 s
2
2
2
2
2
Einsetzen:
1
2 1
2 1
2 1
m1 v1s ' + m2 −v1s ' = m1 v1s + m2 −v1s
2
2
2
2
v1s ' = v1s
⇒
Die Beträge
bleiben gleich!
v2 s ' = v2 s
v2 s
v1s '
v2 s '
2
Kreis mit
Radius v1/2
v1s
m1 ≠ m2 , v1 ≠ 0, v2 ≠ 0
Allgemeiner Fall:
Als Endzustände sind alle
entgegengesetzten Vektoren
mit Spitzen auf dem Kreis erlaubt!
m1 > m2
v2 '
v1
vs
v1 '
v2s '
v1s
v1s '
v2
v2s
Im Schwerpunktsystem
bleiben beim
elastischen Stoß
die Beträge der
Geschwindigkeiten
der Körper erhalten;
da der Gesamtimpuls
Null ist, sind sie immer
entgegengesetzt
ausgerichtet.